

所属成套资源:新人教a版数学必修第二册PPT课件+教案+导学案+分层作业(原卷+解析卷)(含章末总结和知识点)
高中人教A版 (2019)10.1 随机事件与概率精品教学设计
展开这是一份高中人教A版 (2019)10.1 随机事件与概率精品教学设计,共12页。教案主要包含了类题通法,巩固练习1,巩固练习2,巩固练习3,设计意图等内容,欢迎下载使用。
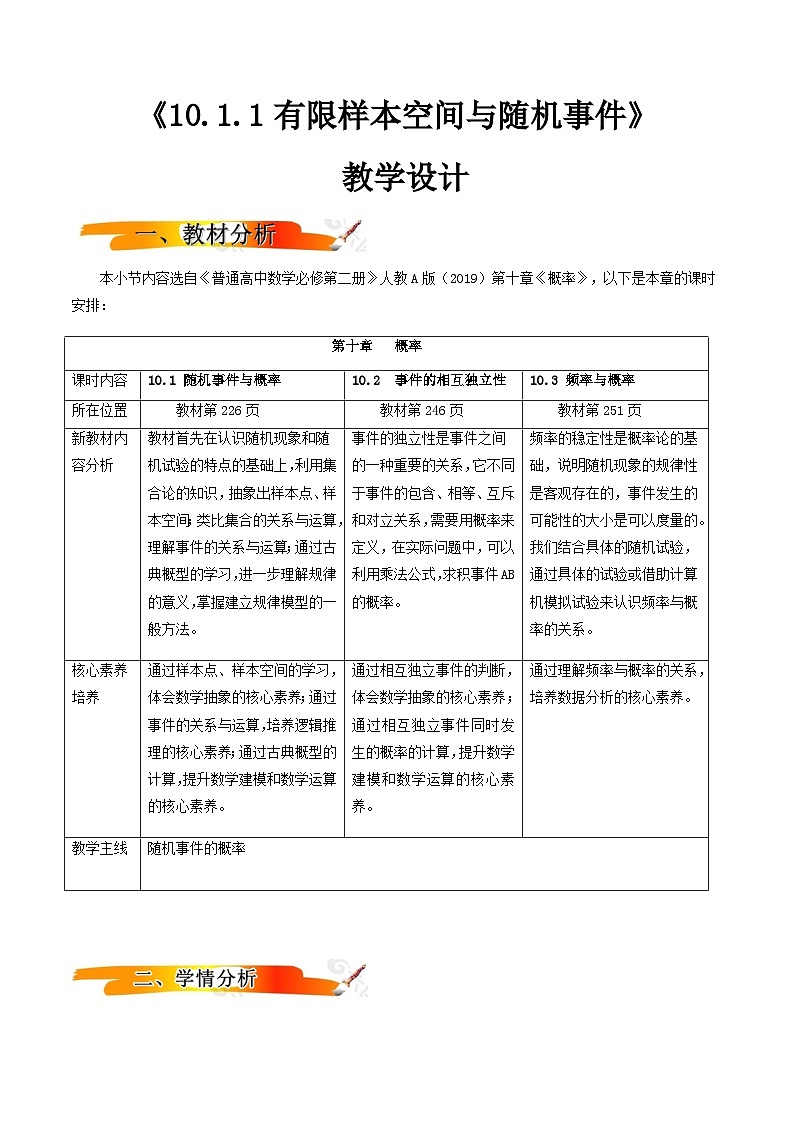
本小节内容选自《普通高中数学必修第二册》人教A版(2019)第十章《概率》,以下是本章的课时安排:
在初中已经初步了解了随机事件的概念,并学习了在试验结果等可能的情形下求简单随机事件的概率,本节我们将进一步研究随机事件,为后面的概率奠定基础。
1.结合具体实例,理解样本点和有限样本空间的含义,培养数学抽象的核心素养;
2.理解随机事件与样本点的关系,了解必然事件、不可能事件的概念,培养数学抽象的核心素养;
3.会求简单随机试验的样本空间,培养逻辑推理的核心素养。
1.重点:写出事件的样本空间
2.难点:判断必然事件、不可能事件与随机事件。
(一)新知导入
观察几幅图片:
事件一:常温下石头在一天内被风化.
事件二:木柴燃烧产生热量.
事件三:射击运动员射击一次中十环.
【问题】 以上三个事件一定会发生吗?
【提示】事件一在常温下不可能发生,是不可能事件;事件二一定发生,是必然事件;事件三可能发生,也可能不发生,是随机事件.
(二)样本空间与随机事件
知识点一 随机试验的样本空间
(1)随机试验的定义:对随机现象的实现和对它的观察称为随机试验,简称试验,常用字母E表示.
(2)随机试验的特点:试验可以在相同条件下重复进行;试验的所有可能结果是明确可知的,并且不止一个;每次试验总是恰好出现这些可能结果中的一个,但事先不能确定出现哪一个结果.
(3)样本点与样本空间的定义:把随机试验E的每个可能的基本结果称为样本点,全体样本点的集合称为样本空间(通常用大写希腊字母Ω表示).如果一个随机试验有n个可能结果ω1,ω2,…,ωn,则称样本空间Ω={ω1,ω2,…,ωn}为有限样本空间.
【做一做】一个家庭有两个小孩,则样本空间为( )
A.{(男,女),(男,男),(女,女)}
B.{(男,女),(女,男)}
C.{(男,男),(男,女),(女,男),(女,女)}
D.{(男,男),(女,女)}
【解析】两个小孩的所有结果是:男男,男女,女男,女女,所有样本空间为{(男,男),(男,女),(女,男),(女,女)}.
【答案】C
知识点二 随机事件
(1)将样本空间的子集称为随机事件,简称事件,只包含一个样本点的事件称为基本事件,随机事件一般用大写字母A,B,C,…表示.
(2)在每次随机试验中,当且仅当A中某个样本点出现时,称为事件A发生.Ω包含了所有的样本点,在每次随机试验中总有一个样本点发生,所以Ω总会发生,称Ω为必然事件,而空集∅不包含任何样本点,在每次试验中,都不会发生,称∅为不可能事件.
【思考1】事件的分类是确定的吗?
【提示】 事件的分类是相对于条件来讲的,在条件变化时,必然事件、随机事件、不可能事件可以相互转化.
【思考2】必然事件与不可能事件具有随机性吗?
【提示】 必然事件与不可能事件不具有随机性.为了统一处理,将必然事件和不可能事件作为随机事件的两个极端情形.
【做一做】判断下列事件是否为随机事件.
(1)长度为3,4,5的三条线段可以构成一个三角形.(×)
(2)长度为2,3,4的三条线段可以构成一直角三角形.(×)
(3)方程x2+2x+3=0有两个不相等的实根.(×)
(4)函数y=lgax(a>0且a≠1)在定义域上为增函数.(√)
(三)典型例题
1.事件类型的判断
例1.指出下列事件是必然事件、不可能事件还是随机事件:
(1)某人购买福利彩票一注,中奖500万元;
(2)三角形的内角和为180°;
(3)没有空气和水,人类可以生存下去;
(4)同时抛掷两枚硬币一次,都出现正面向上;
(5)从分别标有1,2,3,4的四张标签中任取一张,抽到1号标签;
(6)科学技术达到一定水平后,不需任何能量的“永动机”将会出现.
【解】(1)购买一注彩票,可能中奖,也可能不中奖,所以是随机事件.
(2)所有三角形的内角和均为180°,所以是必然事件.
(3)空气和水是人类生存的必要条件,没有空气和水,人类无法生存,所以是不可能事件.
(4)同时抛掷两枚硬币一次,不一定都是正面向上,所以是随机事件.
(5)任意抽取,可能得到1,2,3,4号标签中的任一张,所以是随机事件.
(6)由能量守恒定律可知,不需任何能量的“永动机”不会出现,所以是不可能事件.
【类题通法】判断一个事件是哪类事件的方法
判断一个事件是哪类事件要看两点:一看条件,因为三种事件都是相对于一定条件而言的;二看结果是否发生,一定发生的是必然事件,不一定发生的是随机事件,一定不发生的是不可能事件.
【巩固练习1】(1)下面的事件:①在标准大气压下,水加热到80℃时会沸腾;②a,b∈R,则ab=ba;③一枚硬币连掷两次,两次都出现正面向上.其中是不可能事件的为( )
A.② B.① C.①② D.③
(2)给出下列四个命题:①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件;②当“x为某一实数时可使x2<0”是不可能事件;③“2025年的国庆节是晴天”是必然事件;④“从100个灯泡(有10个是次品)中取出5个,5个都是次品”是随机事件.其中正确命题的个数是( )
A.4 B.3 C.2 D.1
【解析】(1)②是必然事件,③是随机事件.
(2)“2025年的国庆节是晴天”是随机事件,故命题③错误,命题①②④正确.
【答案】( 1)B (2)B
2.样本点与样本空间
例2.分别写出下列试验的样本空间:
(1)某人射击一次,命中的环数;
(2)从装有大小相同但颜色不同的a,b,c,d这4个球的袋中,任取1个球;
(3)从装有大小相同但颜色不同的a,b,c,d这4个球的袋中,任取2个球.
【解】(1)确定样本点,用0表示未命中,i(i=1,2,3,4,5,6,7,8,9,10)表示命中i环,则样本空间为{0,1,2,3,4,5,6,7,8,9,10}.
(2)任取1个球,样本空间为{a,b,c,d}.
(3)任取2个球,记(a,b)表示一次试验中取出的球是a和b,则样本空间为{(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)}.
【类题通法】列举试验的所有样本点的方法
(1)结果是相对于条件而言的,要弄清试验的结果,必须首先明确试验中的条件.
(2)根据日常生活经验,按照一定的顺序列举出所有可能的结果,可应用画树状图、列表等方法解决.
【巩固练习2】袋中装有大小相同的红、白、黄、黑4个球,分别写出以下随机试验的条件和样本空间.
(1)从中任取1球;
(2)从中任取2球.
【解】(1)条件为:从袋中任取1球.样本空间为{红,白,黄,黑}.
(2)条件为:从袋中任取2球.若记(红,白)表示一次试验中,取出的是红球与白球,样本空间为{(红,白),(红,黄),(红,黑),(白,黄),(白,黑),(黄,黑)}.
3.样本点的探求方法
例3.将一枚骰子先后抛掷两次,则:
(1)样本空间一共包含多少个样本点?
(2)记事件A:出现的点数之和大于8,那么事件A包含几个样本点?
【解】法一(列举法):
(1)用(x,y)表示样本点,其中x表示第1枚骰子出现的点数,y表示第2枚骰子出现的点数,则试验的样本空间为Ω={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)},共有36个样本点.
(2)A={(3,6),(4,5),(4,6),(5,4),(5,5),(5,6),(6,3),(6,4),(6,5),(6,6)},共10个样本点.
法二(列表法):
(1)列表如下,可以看出掷第一颗骰子的样本点有6种,第二颗骰子也有6个不同样本点.如第一颗掷得2点时,与第二颗配对的有(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)6个不同样本点,因此两颗骰子配对共有6×6=36个样本点.
(2)从表中看出,A={(3,6),(4,5),(4,6),(5,4),(5,5),(5,6),(6,3),(6,4),(6,5),(6,6)},共10个样本点.
法三(坐标系法):
如图所示,坐标平面内的数表示相应两次抛掷后出现的点数的和,样本点与所描点一一对应.
(1)由图知,样本空间一共包含36个样本点.
(2)事件A包含10个样本点(已用虚线圈出).
法四(树形图法):
一枚骰子先后抛掷两次的所有样本点用树形图表示.如下图所示:
(1)由图知,样本空间共包含36个样本点.
(2)事件A:点数之和大于8包含10个样本点(已用“√”标出).
【类题通法】样本点的四个探求方法
(1)列举法:列举法也称枚举法.即把试验的全部样本点一一列举出来.对于一些情境比较简单,样本点个数不是很多的试验问题,计算时只需一一列举即可得出样本空间和随机事件所含的样本点个数.但列举时必须按一定顺序,做到不重不漏.
(2)列表法:将样本点用表格的方式表示出来,通过表格可以弄清样本点的总数,以及要求的事件所包含的样本点个数.列表法适用于较简单的试验的题目.
(3)坐标系法:通常把对问题的思考分析归结为“有序实数对”,以便更直接地找出样本点个数.列表法的优点是准确、全面、不易遗漏.
(4)树形图法:使用树状的图形把样本点列举出来.树形图法便于分析样本点间的结构关系,适用于较复杂的试验的题目.
【巩固练习3】做抛掷红、蓝两枚骰子的试验,用(x,y)表示结果,其中x表示红色骰子出现的点数,y表示蓝色骰子出现的点数.写出:
(1)这个试验的样本空间;
(2)这个试验的结果的个数;
(3)指出事件A={(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)}的含义.
【解】(1)这个试验的样本空间Ω为
{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}.
(2)这个试验的结果的个数为36.
(3)事件A的含义为抛掷红、蓝两枚骰子,掷出的点数之和为7.
(四)操作演练 素养提升
1、从含有10件正品、2件次品的12件产品中,任意抽取3件,则必然事件是( )
A.3件都是正品B.3件都是次品
C.至少有1件次品D.至少有1件正品
2.下列事件中随机事件的个数为( )
①明天是阴天;
②方程x2+2x+5=0有两个不相等的实根;
③明年长江武汉段的最高水位是29.8 m;
④一个三角形的大边对小角,小边对大角.
A.1 B.2 C.3 D.4
3.抛掷两枚骰子一次,记第一枚骰子掷出的点数与第二枚骰子掷出的点数之差为X,则“X≥5”表示的试验结果是( )
A.第一枚6点,第二枚2点 B.第一枚5点,第二枚1点
C.第一枚1点,第二枚6点 D.第一枚6点,第二枚1点
4.有红、黄、蓝三种颜色的旗帜各3面,在每种颜色的3面旗帜上分别标上号码1、2和3,现任取3面,事件“三面旗帜的颜色与号码均不相同”所包含的样本点的个数是________.
【答案】1.D 2.B 3.D 4.6
【设计意图】通过练习巩固本节所学知识,通过学生解决问题的能力,感悟其中蕴含的数学思想,增强学生的应用意识。
(五)课堂小结,反思感悟
1.知识总结:
2.学生反思:
(1)通过这节课,你学到了什么知识?
(2)在解决问题时,用到了哪些数学思想?
【设计意图】
通过总结,让学生进一步巩固本节所学内容,提高概括能力,提高学生的数学运算能力和逻辑推理能力。
完成教材:第229页 练习 第1,2,3题
第243页 习题10.1 第1,2题
第十章 概率
课时内容
10.1 随机事件与概率
10.2 事件的相互独立性
10.3 频率与概率
所在位置
教材第226页
教材第246页
教材第251页
新教材内容分析
教材首先在认识随机现象和随机试验的特点的基础上,利用集合论的知识,抽象出样本点、样本空间;类比集合的关系与运算,理解事件的关系与运算;通过古典概型的学习,进一步理解规律的意义,掌握建立规律模型的一般方法。
事件的独立性是事件之间的一种重要的关系,它不同于事件的包含、相等、互斥和对立关系,需要用概率来定义,在实际问题中,可以利用乘法公式,求积事件AB的概率。
频率的稳定性是概率论的基础,说明随机现象的规律性是客观存在的,事件发生的可能性的大小是可以度量的。我们结合具体的随机试验,通过具体的试验或借助计算机模拟试验来认识频率与概率的关系。
核心素养培养
通过样本点、样本空间的学习,体会数学抽象的核心素养;通过事件的关系与运算,培养逻辑推理的核心素养;通过古典概型的计算,提升数学建模和数学运算的核心素养。
通过相互独立事件的判断,体会数学抽象的核心素养;通过相互独立事件同时发生的概率的计算,提升数学建模和数学运算的核心素养。
通过理解频率与概率的关系,培养数据分析的核心素养。
教学主线
随机事件的概率
第二颗
第一颗
1
2
3
4
5
6
1
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
2
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
3
(3,1)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
4
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(4,6)
5
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
(5,6)
6
(6,1)
(6,2)
(6,3)
(6,4)
(6,5)
(6,6)
相关教案
这是一份人教A版 (2019)必修 第二册10.1 随机事件与概率教学设计,共5页。
这是一份人教A版 (2019)必修 第二册10.1 随机事件与概率教案设计,共5页。
这是一份高中数学人教A版 (2019)必修 第二册10.1 随机事件与概率教案,共3页。教案主要包含了教学重难点,教学过程,板书设计等内容,欢迎下载使用。













