初中数学3 正方形的性质与判定当堂达标检测题

这是一份初中数学3 正方形的性质与判定当堂达标检测题，文件包含北师大版数学九上同步讲义专题03正方形的性质与判定3个知识点8种题型1个易错点中考2种考法原卷版docx、北师大版数学九上同步讲义专题03正方形的性质与判定3个知识点8种题型1个易错点中考2种考法解析版docx等2份试卷配套教学资源，其中试卷共113页， 欢迎下载使用。

倍速学习五种方法
【方法一】 脉络梳理法
知识点1：正方形的定义
知识点2：正方形的性质（重难点）
知识点3：正方形的判定（重难点）
【方法二】 实例探索法
题型1：由正方形的性质求角的度数
题型2：由正方形的性质求线段的长度
题型3：由正方形的性质证明线段相等
题型4：由正方形的性质解决正方形的周长与面积问题
题型5：正方形的判定
题型6：正方形的性质与判定综合运用
题型7：与正方形有关的动态问题
题型8：与正方形有关的存在性问题
【方法三】 差异对比法
易错点1正方形的性质运用不正确导致出错
【方法四】 仿真实战法
考法1：正方形性质
考法2：正方形判定
【方法五】 成果评定法
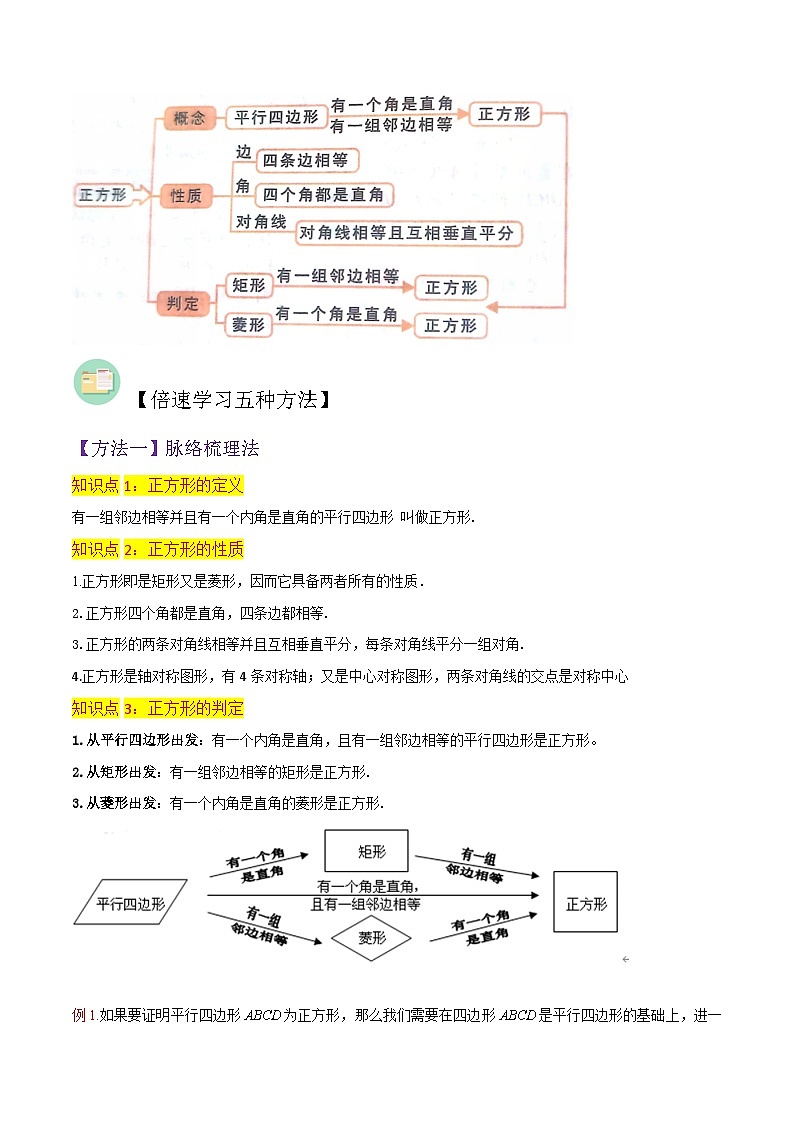
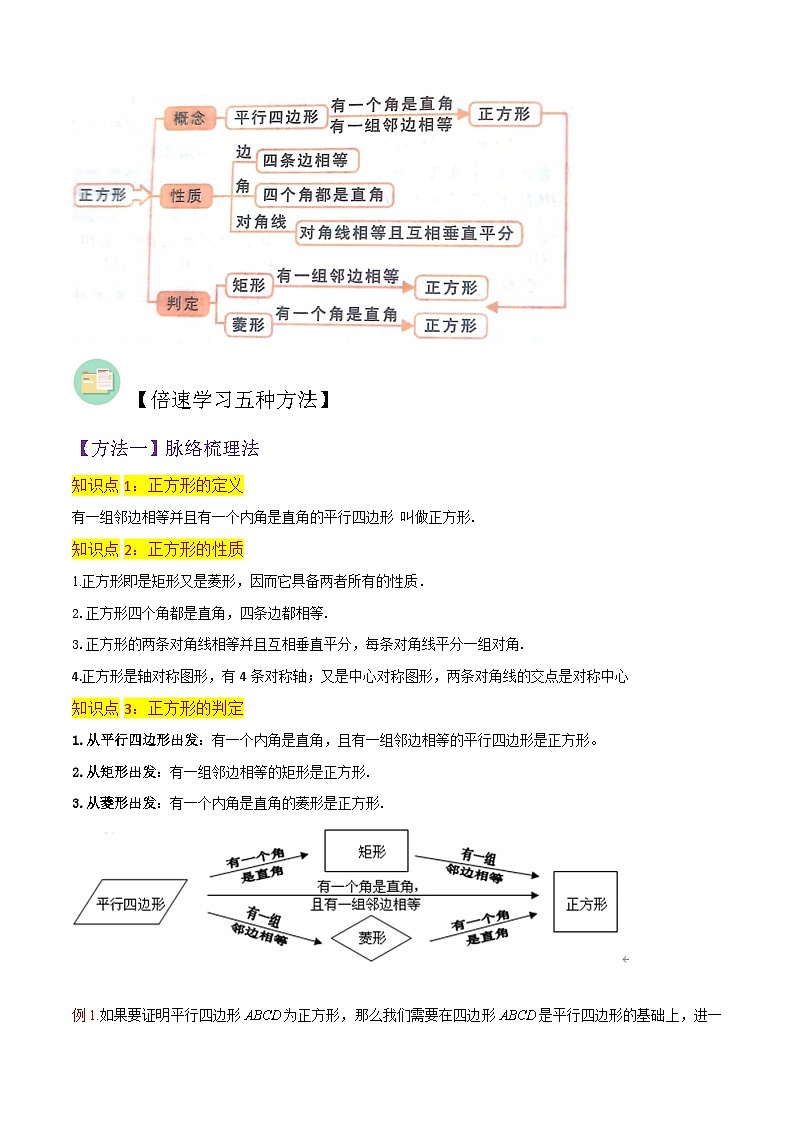
【知识导图】
【倍速学习五种方法】
【方法一】脉络梳理法
知识点1：正方形的定义
有一组邻边相等并且有一个内角是直角的平行四边形 叫做正方形.
知识点2：正方形的性质
1.正方形即是矩形又是菱形，因而它具备两者所有的性质．
2.正方形四个角都是直角，四条边都相等.
3.正方形的两条对角线相等并且互相垂直平分，每条对角线平分一组对角.
4.正方形是轴对称图形，有4条对称轴；又是中心对称图形，两条对角线的交点是对称中心
知识点3：正方形的判定
1.从平行四边形出发：有一个内角是直角，且有一组邻边相等的平行四边形是正方形。
2.从矩形出发：有一组邻边相等的矩形是正方形.
3.从菱形出发：有一个内角是直角的菱形是正方形.
例1.如果要证明平行四边形为正方形，那么我们需要在四边形是平行四边形的基础上，进一步证明（ ）
A．AB=AD且AC⊥BD B．AB=AD且AC=BD
C．∠A=∠B且AC=BD D．AC和BD互相垂直平分
【答案】B
【解析】 B答案中，AB=AD可知平行四边形是菱形，而AC = BD可知平行四边形是矩形，则
平行四边形为正方形．
【总结】考察正方形的判定方法的运用．
【方法二】实例探索法
题型1：由正方形的性质求角的度数
例2.（1）如图（1），已知P正方形ABCD对角线BD上一点，且BP=BC，则度数是 ；
（2）如图（2），正方形ABCD的对角线AC、BD相交于点O，E是OB延长线上一点，
CE=BD，∠ECB的度数是_______．
A
B
C
D
E
O
（2）
（1）
【答案】（1）22.5°；（2）15°．
【解析】（1）∵正方形ABCD，∴．
∵BP=BC，∴．
∵，∴；
（2）联结
∵，∴．∵，∴
∵，∴，∴．
∵，∴．
【总结】考察正方形的性质的运用．
例3.正方形ABCD被两条分别与边AB、BC平行的线段EF、GH分割成4个小矩形，P
是EF与GH的交点，若矩形PFCH的面积恰好是矩形AGPE面积的2倍，求∠HAF的大小．
A
B
C
D
E
F
G
H
P
M
【答案】45°，理由见解析．
【解析】延长到，使得，联结
则
∴，
∴
设正方形的边长为，，，则，
∵矩形PFCH的面积恰好是矩形AGPE面积的2倍，
∴
而在直角三角形中，
则可得：，∴
∵，∴
∴， ∴．
【总结】考察正方形的性质及勾股定理的综合应用，注意对正方形背景下的辅助线的添加方
法进行归纳总结．
题型2：由正方形的性质求线段的长度
例4.如图，已知有一块面积为1的正方形ABCD，M、N分别为AD、BC上的中点，将点C折到MN上，落在P点的位置，折痕为BQ，连结PQ．
求：（1） MP的长；（2）PQ的长．
【解析】（1）由翻折性质，可得垂直平分，∴
∵M、N分别为AD、BC上的中点，且正方形ABCD，∴，
∴，即为等边三角形
∵，，
∴，；
由题意可得：，
在直角三角形中，，，
∴，∴．
题型3：由正方形的性质证明线段相等
例5.如图，正方形ABCD的对角线AC上截取CE=CD，作EF⊥AC交AD于点F．求证：AE=EF=FD．
A
B
C
D
E
F
【解析】∵正方形ABCD，EF⊥AC， ∴．
∵，，∴
∴
∵，，∴
∴，∴．
【总结】考察正方形的性质及直角三角形全等的判定的综合运用．
例6.如图，已知E是正方形ABCD的边BC上的任意一点，BF⊥AE，垂足为G，交CD于点F．求证：AE=BF．
A
B
C
D
E
F
G
【解析】∵BF⊥AE，∴
∵，∴
∵，，
∴， ∴．
【总结】考察正方形的性质的运用
例7.已知：Q为正方形ABCD的CD边的中点，P为CD上一点，且∠BAP=2∠QAD．求证：AP=PC+BC．
【解析】延长到，使得，连接交BC于F．
∵，CD=AB， ∴CE=AB
∵∠ECF=∠B，∠CFE=∠AFB
∴△ABF≌△ECF
∴BF=CF，即
∵Q为正方形ABCD的CD边的中点，
∴．∵BC=CD，∴DQ=BF
∵DQ=BF，∠B=∠D，AB=AD， ∴△ABF≌△ADQ， ∴∠QAD=∠BAF，
∵∠BAP =∠BAF+∠PAF，∠BAP = 2∠QAD，∠QAD=∠BAF，∴∠BAF=∠PAF
∵AB∥CD，∴∠BAF=∠E， ∴∠E=∠PAF， ∴PE=AP
∵PE=PC+CE，CE=BC， ∴
【总结】考察正方形的性质的运用，注意辅助线的添加．
例8.已知：在正方形ABCD中，M为AB的中点，MN⊥MD，BN平分∠CBE并交MN于N．求证：MD=MN．
A
B
C
D
E
M
N
G
【解析】取的中点，联结
∵M为AB的中点，∴
∵为的中点，∴
∵，∴
∵BN平分∠CBE，∴，∴
∵，∴，∴，∴
∵MN⊥MD，∴，又∵，∴
∵，，
∴，∴
【总结】考察正方形的性质的综合运用，注意辅助线的添加．
题型4：由正方形的性质解决正方形的周长与面积问题
例9.已知：如图边长为的正方形的对角线、交于点，、分别为、上的点，且．
求证：（1）．
（2）、分别在、延长线上，，四边形与正方形重合部分的面积等于．
【解析】（1）∵，，
∴∴
∵，∴，
即；
（2）∵，∴
∴四边形与正方形重合部分的面积等于
．
【总结】考察正方形的性质运用，注意第（2）问中将面积进行转化．
题型5：正方形的判定
例10.如图所示，已知矩形ABCD的各内角平分线AQ、DF、BE、CH分别交BC、AD于点Q、F、E、H，试证明
它们组成的四边形MNPO是正方形．
【思路点拨】矩形的各内角平分线将每个内角分成45°，它们和矩形的边组成了等腰直角三角形，所以围成的图形为矩形，再证明一组邻边相等，得出结论．
【答案与解析】
解：∵ 四边形ABCD为矩形，
∴ AD＝BC，∠DAB＝∠ABC＝90°，
∴ ∠1＝∠2＝∠DAB＝45°，∠3＝∠4＝∠ABC＝45°，
∴ ∠OMN＝∠AMB＝90°．
同理∠MNP＝90°，∠NPO＝90°，
∴ 四边形MNPO为矩形．
又∵ ∠2＝∠4，∠5＝∠6，AD＝BC，
∴ △AOD≌△BNC，
∴ AO＝BN．
又∵ ∠1＝∠3，∴ AM＝BM，
∴ AO－AM＝BN－BM，即MN＝MO．
∴ 矩形MNPO为正方形．
【总结升华】(1)灵活运用角平分线的性质，等腰直角三角形的性质及判定，矩形的判定方法和正方形的判定方法．(2)本题解题思路：矩形＋邻边相等正方形．
题型6：正方形的性质与判定综合运用
例11.如图，在线段上取一点，使，以、为边在同侧作正方形和，在上取，在的延长线上取一点，使．
求证：四边形为正方形．
【解析】∵

又，
∴
∴，∴四边形是菱形，
∵，∴，
∴，∴菱形是正方形．
【总结】考察正方形的性质及判定方法的综合运用．
题型7：与正方形有关的动态问题
例12.如图（1）所示，四边形ABCD是由两个全等的等腰直角三角形斜边重合在一起组成的平面图形．如图（2）所示，点P是边BC上一点，PH⊥BC交BD于点H，连接AP交BD于点E，点F为DH中点，连接AF；
（1）求证：四边形ABCD为正方形；
M
（2）当点P在线段BC上运动时，∠PAF的大小是否会发生变化？若不变，请求出∠PAF的值；若变化，请说明理由；
（3）求证：．
【解析】
（1）∵四边形ABCD是由两个全等的等腰直角三角形斜边重合在一起组成的平面图形．
∴，
∴四边形ABCD为正方形
（2）不变化．
联结，并延长交的延长线于，联结
∵，∴，
∴
∵点F为DH中点，∴
∵，，
∴，∴，
∵，∴
∵，∴，
∴
∴，∴
∵，，
∴，
∴，
∴
∴是等腰直角三角形
∵，∴．
即当点P在线段BC上运动时，∠PAF的大小不会发生变化；
（3）在上截取，联结
∵是等腰直角三角形
∴
∵，，
∴
∴，
∴
在直角△中，
∵，
∴
∴
∵，，
∴
∴
∵，，
∴．
【总结】本题综合性比较强，主要考查了正方形的性质和判定的综合运用，解题时注意分析角度之间的关系．
题型8：与正方形有关的探究问题
例13.如图四边形ABCD是正方形，点E、K分别在BC，AB上，点G在BA的延长线上，且CE＝BK＝AG．以线
段DE、DG为边作DEFG．
(1)求证：DE＝DG，且DE⊥DG．
(2)连接KF，猜想四边形CEFK是怎样的特殊四边形，并证明你的猜想．
【答案】
证明：(1)∵ 四边形ABCD是正方形，
∴ DC＝DA，∠DCE＝∠DAG＝90°．
又∵ CE＝AG，
∴ △DCE≌△DAG，
∴ ∠EDC＝∠GDA，DE＝DG．
又∵ ∠ADE＋∠EDC＝90°，
∴ ∠ADE＋∠GDA＝90°，
∴ DE⊥DG．
(2)四边形CEFK为平行四边形．
证明：设CK，DE相交于M点，
∵ 四边形ABCD和四边形DEFG都是正方形，
∴ AB∥CD，AB＝CD，EF＝DG，EF∥DG；
∵ BK＝AG，∴ KG＝AB＝CD．
∴ 四边形CKGD为平行四边形．
∴ CK＝DG＝EF，CK∥DG∥EF
∴ 四边形CEFK为平行四边形．
例14.如图，在正方形中，点在边上（点与点、不重合），过点作， 与边相交于点，与边的延长线相交于点．
（1）由几个不同的位置，分别测量、、的长，从中你能发现、、的数量之间具有怎样的关系？并证明你所得到的结论．
（2）联结，如果正方形的边长为2，设，的面积为，求与之间的函数解析式，并写出函数的定义域．
（3）如果正方形的边长为2，的长为，求点到直线的距离．
【答案】（1）；（2）（）；（3）．
【解析】（1）证明：过点作，垂足为
∵，
∴四边形是矩形
∴
∵，∴
∵，，
∴
∴，即
∵，∴
∵，
∴
∵，∴，定义域为
（3）联结，作于
∴
∵，
∴，∴
∴点到直线的距离为．
【总结】本题综合性较强，主要考察正方形的性质和勾股定理的综合应用，解题时注意利用
等积法求线段的长．
【方法三】差异对比法
易错点1：正方形的性质运用不正确导致出错
例15.如图所示，菱形PQRS内接于矩形ABCD，使得点P、Q、R、S分别为边AB、BC、CD、DA上的点．已知PB=15，BQ=20，PR=30，QS=40．求矩形ABCD的周长．
【答案】．
【解析】∵，∴
∵，∴
∴，
即
∵，，
∴
∴
也可证得：，∴
设
∵与互相垂直平分，这样得到8个直角三角形，且其中6个三角形的边长分别
为15、20、25，而，，则直角△ASP和直角△CQR的三边分别为，矩形面积等于8个直角三角形面积之和．
所以，
则有而，解得：，或，
当时，与不合，所以舍去；
∴矩形的周长为．
【总结】考察特殊的平行四边形的性质及面积法的综合应用．
【方法四】 仿真实战法
考法1：正方形性质
1．（2022•黄石）如图，正方形OABC的边长为，将正方形OABC绕原点O顺时针旋转45°，则点B的对应点B1的坐标为（ ）
A．（﹣，0）B．（，0）C．（0，）D．（0，2）
【分析】连接OB，由正方形的性质和勾股定理得OB＝2，再由旋转的性质得B1在y轴正半轴上，且OB1＝OB＝2，即可得出结论．
【解答】解：如图，连接OB，
∵正方形OABC的边长为，
∴OC＝BC＝，∠BCO＝90°，∠BOC＝45°，
∴OB＝＝＝2，
∵将正方形OABC绕原点O顺时针旋转45°后点B旋转到B1的位置，
∴B1在y轴正半轴上，且OB1＝OB＝2，
∴点B1的坐标为（0，2），
故选：D．
【点评】本题考查了正方形的性质、旋转的性质、坐标与图形性质以及勾股定理等知识，熟练掌握正方形的性质和旋转的性质是解题的关键．
2．（2022•广州）如图，正方形ABCD的面积为3，点E在边CD上，且CE＝1，∠ABE的平分线交AD于点F，点M，N分别是BE，BF的中点，则MN的长为（ ）
A．B．C．2﹣D．
【分析】连接EF，由正方形ABCD的面积为3，CE＝1，可得DE＝﹣1，tan∠EBC＝＝＝，即得∠EBC＝30°，又AF平分∠ABE，可得∠ABF＝∠ABE＝30°，故AF＝＝1，DF＝AD﹣AF＝﹣1，可知EF＝DE＝×（﹣1）＝﹣，而M，N分别是BE，BF的中点，即得MN＝EF＝．
【解答】解：连接EF，如图：
∵正方形ABCD的面积为3，
∴AB＝BC＝CD＝AD＝，
∵CE＝1，
∴DE＝﹣1，tan∠EBC＝＝＝，
∴∠EBC＝30°，
∴∠ABE＝∠ABC﹣∠EBC＝60°，
∵AF平分∠ABE，
∴∠ABF＝∠ABE＝30°，
在Rt△ABF中，AF＝＝1，
∴DF＝AD﹣AF＝﹣1，
∴DE＝DF，△DEF是等腰直角三角形，
∴EF＝DE＝×（﹣1）＝﹣，
∵M，N分别是BE，BF的中点，
∴MN是△BEF的中位线，
∴MN＝EF＝．
故选：D．
【点评】本题考查正方形性质及应用，涉及含30°角的直角三角形三边关系，等腰直角三角形三边关系，解题的关键是根据已知求得∠EBC＝30°．
3．（2022•青岛）如图，O为正方形ABCD对角线AC的中点，△ACE为等边三角形．若AB＝2，则OE的长度为（ ）
A．B．C．D．
【分析】首先利用正方形的性质可以求出AC，然后利用等边三角形的性质可求出OE．
【解答】解：∵四边形ABCD为正方形，AB＝2，
∴AC＝2，
∵O为正方形ABCD对角线AC的中点，△ACE为等边三角形，
∴∠AOE＝90°，
∴AC＝AE＝2，AO＝，
∴OE＝×＝．
故选：B．
【点评】本题主要考查了正方形的性质，同时也利用了等边三角形的性质，有一定的综合性．
4．（2022•泰州）如图，正方形ABCD的边长为2，E为与点D不重合的动点，以DE为一边作正方形DEFG．设DE＝d1，点F、G与点C的距离分别为d2、d3，则d1+d2+d3的最小值为（ ）
A．B．2C．2D．4
【分析】连接AE，那么，AE＝CG，所以这三个d的和就是AE+EF+FC，所以大于等于AC，故当AEFC四点共线有最小值，最后求解，即可求出答案．
【解答】解：如图，连接AE，
∵四边形DEFG是正方形，
∴∠EDG＝90°，EF＝DE＝DG，
∵四边形ABCD是正方形，
∴AD＝CD，∠ADC＝90°，
∴∠ADE＝∠CDG，
∴△ADE≌△CDG（SAS），
∴AE＝CG，
∴d1+d2+d3＝EF+CF+AE，
∴点A，E，F，C在同一条线上时，EF+CF+AE最小，即d1+d2+d3最小，
连接AC，
∴d1+d2+d3最小值为AC，
在Rt△ABC中，AC＝AB＝2，
∴d1+d2+d3最小＝AC＝2，
故选：C．
【点评】此题主要考查了正方形的性质，全等三角形的判定和性质，正确作出辅助线是解本题的关键．
5．（2022•黔东南州）如图，在边长为2的等边三角形ABC的外侧作正方形ABED，过点D作DF⊥BC，垂足为F，则DF的长为（ ）
A．2+2B．5﹣C．3﹣D．+1
【分析】方法一：如图，延长DA、BC交于点G，利用正方形性质和等边三角形性质可得：∠BAG＝90°，AB＝2，∠ABC＝60°，运用解直角三角形可得AG＝2，DG＝2+2，再求得∠G＝30°，根据直角三角形性质得出答案．
方法二：过点E作EG⊥DF于点G，作EH⊥BC于点H，利用解直角三角形可得EH＝1，BH＝，再证明△BEH≌△DEG，可得DG＝BH＝，即可求得答案．
【解答】解：方法一：如图，延长DA、BC交于点G，
∵四边形ABED是正方形，
∴∠BAD＝90°，AD＝AB，
∴∠BAG＝180°﹣90°＝90°，
∵△ABC是边长为2的等边三角形，
∴AB＝2，∠ABC＝60°，
∴AG＝AB•tan∠ABC＝2×tan60°＝2，
∴DG＝AD+AG＝2+2，
∵∠G＝90°﹣60°＝30°，DF⊥BC，
∴DF＝DG＝×（2+2）＝1+，
故选D．
方法二：如图，过点E作EG⊥DF于点G，作EH⊥BC于点H，
则∠BHE＝∠DGE＝90°，
∵△ABC是边长为2的等边三角形，
∴AB＝2，∠ABC＝60°，
∵四边形ABED是正方形，
∴BE＝DE＝2，∠ABE＝∠BED＝90°，
∴∠EBH＝180°﹣∠ABC﹣∠ABE＝180°﹣60°﹣90°＝30°，
∴EH＝BE•sin∠EBH＝2•sin30°＝2×＝1，BH＝BE•cs∠EBH＝2cs30°＝，
∵EG⊥DF，EH⊥BC，DF⊥BC，
∴∠EGF＝∠EHB＝∠DFH＝90°，
∴四边形EGFH是矩形，
∴FG＝EH＝1，∠BEH+∠BEG＝∠GEH＝90°，
∵∠DEG+∠BEG＝90°，
∴∠BEH＝∠DEG，
在△BEH和△DEG中，
，
∴△BEH≌△DEG（AAS），
∴DG＝BH＝，
∴DF＝DG+FG＝+1，
故选：D．
【点评】本题考查了正方形的性质、等边三角形的性质、全等三角形的判定和性质、解直角三角形，题目的综合性很好，难度不大．
6．（2022•重庆）如图，在正方形ABCD中，对角线AC、BD相交于点O．E、F分别为AC、BD上一点，且OE＝OF，连接AF，BE，EF．若∠AFE＝25°，则∠CBE的度数为（ ）
A．50°B．55°C．65°D．70°
【分析】利用正方形的对角线互相垂直平分且相等，等腰直角三角形的性质，三角形的内角和定理和全等三角形的判定与性质解答即可．
【解答】解：∵四边形ABCD是正方形，
∴∠AOB＝∠AOD＝90°，OA＝OB＝OD＝OC．
∵OE＝OF，
∴△OEF为等腰直角三角形，
∴∠OEF＝∠OFE＝45°，
∵∠AFE＝25°，
∴∠AFO＝∠AFE+∠OFE＝70°，
∴∠FAO＝20°．
在△AOF和△BOE中，
，
∴△AOF≌△BOE（SAS）．
∴∠FAO＝∠EBO＝20°，
∵OB＝OC，
∴△OBC是等腰直角三角形，
∴∠OBC＝∠OCB＝45°，
∴∠CBE＝∠EBO+∠OBC＝65°．
故选：C．
【点评】本题主要考查了正方形的性质，等腰直角三角形的判定与性质，全等三角形的判定与性质，三角形的内角和定理，熟练掌握正方形的性质是解题的关键．
7．（2022•泸州）如图，在边长为3的正方形ABCD中，点E是边AB上的点，且BE＝2AE，过点E作DE的垂线交正方形外角∠CBG的平分线于点F，交边BC于点M，连接DF交边BC于点N，则MN的长为（ ）
A．B．C．D．1
【分析】根据正方形的性质、相似三角形的判定和性质，可以求得CN和BN的长，然后根据BC＝3，即可求得MN的长．
【解答】解：作FH⊥BG交于点H，作FK⊥BC于点K，
∵BF平分∠CBG，∠KBH＝90°，
∴四边形BHFK是正方形，
∵DE⊥EF，∠EHF＝90°，
∴∠DEA+∠FEH＝90°，∠EFH+∠FEH＝90°，
∴∠DEA＝∠EFH，
∵∠A＝∠EHF＝90°，
∴△DAE∽△EHF，
∴，
∵正方形ABCD的边长为3，BE＝2AE，
∴AE＝1，BE＝2，
设FH＝a，则BH＝a，
∴，
解得a＝1；
∵FK⊥CB，DC⊥CB，
∴△DCN∽△FKN，
∴，
∵BC＝3，BK＝1，
∴CK＝2，
设CN＝b，则NK＝2﹣b，
∴，
解得b＝，
即CN＝，
∵∠A＝∠EBM，∠AED＝∠BME，
∴△ADE∽△BEM，
∴，
∴，
解得BM＝，
∴MN＝BC﹣CN﹣BM＝3﹣﹣＝，
故选：B．
【点评】本题考查正方形的性质、相似三角形的判定和性质，解答本题的关键是明确题意，利用数形结合的思想解答．
8．（2022•益阳）如图，将边长为3的正方形ABCD沿其对角线AC平移，使A的对应点A′满足AA′＝AC，则所得正方形与原正方形重叠部分的面积是 4 ．
【分析】由正方形边长为3，可求AC＝3，则AA′＝AC＝，由平移可得重叠部分是正方形，根据正方形的面积公式可求重叠部分面积．
【解答】解：∵正方形ABCD的边长为3，
∴AC＝3，
∴AA′＝AC＝，
∴A′C＝2，
由题意可得重叠部分是正方形，且边长为2，
∴S重叠部分＝4．
故答案为：4．
【点评】本题考查了正方形的性质，平移的性质，关键是灵活运用这些性质解决问题．
9．（2022•海南）如图，正方形ABCD中，点E、F分别在边BC、CD上，AE＝AF，∠EAF＝30°，则∠AEB＝ 60 °；若△AEF的面积等于1，则AB的值是 ．
【分析】利用“HL”先说明△ABE与△ADF全等，得结论∠BAE＝∠DAF，再利用角的和差关系及三角形的内角和定理求出∠AEB；先利用三角形的面积求出AE，再利用直角三角形的边角间关系求出AB．
【解答】解：∵四边形ABCD是正方形，
∴AB＝AD，∠BAD＝∠B＝∠D＝90°．
在Rt△ABE和Rt△ADF中，
，
∴Rt△ABE≌Rt△ADF（HL）．
∴∠BAE＝∠DAF．
∴∠BAE＝（∠BAD﹣∠EAF）
＝（90°﹣30°）
＝30°．
∴∠AEB＝60°．
故答案为：60．
过点F作FG⊥AE，垂足为G．
∵sin∠EAF＝，
∴FG＝sin∠EAF×AF．
∵S△AEF＝×AE×FG＝×AE×AF×sin∠EAF＝1，
∴×AE2×sin30°＝1．
即×AE2×＝1．
∴AE＝2．
在Rt△ABE中，
∵cs∠BAE＝，
∴AB＝cs30°×AE
＝×2
＝．
故答案为：．
【点评】本题主要考查了正方形的性质及解直角三角形，掌握正方形的性质及直角三角形的边角间关系是解决本题的关键．
10．（2022•黔东南州）如图，折叠边长为4cm的正方形纸片ABCD，折痕是DM，点C落在点E处，分别延长ME、DE交AB于点F、G，若点M是BC边的中点，则FG＝ cm．
【分析】如图，连接DF，可证得Rt△DAF≌Rt△DEF（HL），则AF＝EF，设AF＝xcm，则EF＝xcm，利用勾股定理求得x＝，再由△FGE∽△FMB，即可求得答案．
【解答】解：如图，连接DF，
∵四边形ABCD是正方形，
∴AD＝CD＝AB＝BC＝4cm，∠A＝∠B＝∠C＝90°，
∵点M是BC边的中点，
∴CM＝BM＝BC＝2cm，
由折叠得：DE＝CD＝4cm，EM＝CM＝2cm，∠DEM＝∠C＝90°，
∴∠DEF＝180°﹣90°＝90°，AD＝DE，
∴∠A＝∠DEF，
在Rt△DAF和Rt△DEF中，
，
∴Rt△DAF≌Rt△DEF（HL），
∴AF＝EF，
设AF＝xcm，则EF＝xcm，
∴BF＝（4﹣x）cm，FM＝（x+2）cm，
在Rt△BFM中，BF2+BM2＝FM2，
∴（4﹣x）2+22＝（x+2）2，
解得：x＝，
∴AF＝EF＝cm，BF＝4﹣＝cm，FM＝+2＝cm，
∵∠FEG＝∠DEM＝90°，
∴∠FEG＝∠B＝90°，
∵∠EFG＝∠BFM，
∴△FGE∽△FMB，
∴＝，即＝，
∴FG＝cm，
故答案为：．
【点评】此题考查了折叠的性质、正方形的性质、勾股定理、全等三角形的判定和性质、相似三角形的判定与性质．此题有一定难度，注意掌握数形结合思想与方程思想的应用．
11．（2022•广西）如图，在正方形ABCD中，AB＝4，对角线AC，BD相交于点O．点E是对角线AC上一点，连接BE，过点E作EF⊥BE，分别交CD，BD于点F，G，连接BF，交AC于点H，将△EFH沿EF翻折，点H的对应点H′恰好落在BD上，得到△EFH′．若点F为CD的中点，则△EGH′的周长是 5+ ．
【分析】作辅助线，构建全等三角形，先根据翻折的性质得△EGH'≌△EGH，所以△EGH′的周长＝△EGH的周长，接下来计算△EGH的三边即可；证明△BME≌△FNE（ASA）和△BEO≌△EFP（AAS），得OE＝PF＝2，OB＝EP＝4，利用三角函数和勾股定理分别计算EG，GH和EH的长，相加可得结论．
增加解法二：点B为原点建立平面直角坐标系，直线AB为y轴，BC为x轴，从而求出点E，G，H'的坐标，从而得到△EGH'的周长即可．
【解答】解：如图，过点E作EM⊥BC于M，作EN⊥CD于N，过点F作FP⊥AC于P，连接GH，
∵将△EFH沿EF翻折得到△EFH′，
∴△EGH'≌△EGH，
∵四边形ABCD是正方形，
∴AB＝CD＝BC＝4，∠BCD＝90°，∠ACD＝∠ACB＝45°，
∴BD＝BC＝8，△CPF是等腰直角三角形，
∵F是CD的中点，
∴CF＝CD＝2，
∴CP＝PF＝2，OB＝BD＝4，
∵∠ACD＝∠ACB，EM⊥BC，EN⊥CD，
∴EM＝EN，∠EMC＝∠ENC＝∠BCD＝90°，
∴∠MEN＝90°，
∵EF⊥BE，
∴∠BEF＝90°，
∴∠BEM＝∠FEN，
∵∠BME＝∠FNE，
∴△BME≌△FNE（ASA），
∴EB＝EF，
∵∠BEO+∠PEF＝∠PEF+∠EFP＝90°，
∴∠BEO＝∠EFP，
∵∠BOE＝∠EPF＝90°，
∴△BEO≌△EFP（AAS），
∴OE＝PF＝2，OB＝EP＝4，
∵tan∠OEG＝＝，即＝，
∴OG＝1，
∴EG＝＝，
∵OB∥FP，
∴∠OBH＝∠PFH，
∴tan∠OBH＝tan∠PFH，
∴＝，
∴＝＝2，
∴OH＝2PH，
∵OP＝OC﹣PC＝4﹣2＝2，
∴OH＝×2＝，
在Rt△OGH中，由勾股定理得：GH＝＝，
∴△EGH′的周长＝△EGH的周长＝EH+EG+GH＝2+++＝5+．
故答案为：5+．
【点评】本题考查了正方形的判定和性质，全等三角形的判定和性质，解直角三角形，图形的翻折等知识，本题十分复杂，解决问题的关键是关注特殊性，添加辅助线，需要十分扎实的基础和很强的能力．
12．（2022•无锡）如图，正方形ABCD的边长为8，点E是CD的中点，HG垂直平分AE且分别交AE、BC于点H、G，则BG＝ 1 ．
【分析】设CG＝x，则BG＝8﹣x，根据勾股定理可得AB2+BG2＝CE2+CG2，可求得x的值，进而求出BG的长．
【解答】解：连接AG，EG，
∵E是CD的中点，
∴DE＝CE＝4，
设CG＝x，则BG＝8﹣x，
在Rt△ABG和Rt△GCE中，根据勾股定理，得
AB2+BG2＝CE2+CG2，
即82+（8﹣x）2＝42+x2，
解得x＝7，
∴BG＝BC﹣CG＝8﹣7＝1．
故答案是：1．
【点评】本题考查了正方形的性质、全等三角形的判定与性质、线段垂直平分线的性质，解决本题的关键是熟练运用线段垂直平分线的性质构造辅助线．
13．（2022•贵阳）如图，在正方形ABCD中，E为AD上一点，连接BE，BE的垂直平分线交AB于点M，交CD于点N，垂足为O，点F在DC上，且MF∥AD．
（1）求证：△ABE≌△FMN；
（2）若AB＝8，AE＝6，求ON的长．
【分析】（1）首先利用正方形的性质可以得到AB＝AD，∠BAE＝90°，然后利用MF∥AD可以得到∠MFN＝90°，进一步得到∠FMN＝∠MBO，最后利用全等三角形的判定方法即可求解；
（2）通过证明△BOM∽△BAE，可得OM：AE＝BO：BA，可求OM的长，即可求解．
【解答】解：（1）∵四边形ABCD为正方形，
∴AB＝AD，AB∥CD，∠A＝∠D＝90°，
又∵MF∥AD，
∴四边形AMFD为矩形，
∴∠MFD＝∠MFN＝90°，
∴AD＝MF，
∴AB＝MF，
∵BE的垂直平分线交AB于点M，交CD于点N，垂足为O，
∴∠MFN＝∠BAE＝90°，∠FMN+∠BMO＝∠BMO+∠MBO＝90°，
∴∠FMN＝∠MBO，
在△ABE和△FMN中，
∴△ABE≌△FMN（ASA）；
（2）∵∠MOB＝∠A＝90°，∠ABE是公共角，
∴△BOM∽△BAE，
∴OM：AE＝BO：BA，
∵AB＝8，AE＝6，
∴BE＝＝10，
∴OM：6＝5：8，
∴OM＝，
∵△ABE≌△FMN，
∴NM＝BE＝10，
∴ON＝MN﹣MO＝．
【点评】本题主要考查了正方形的性质，垂直平分线的性质相似三角形的判定与性质，综合性比较强，对于学生的要求比较高．
14．（2022•遵义）将正方形ABCD和菱形EFGH按照如图所示摆放，顶点D与顶点H重合，菱形EFGH的对角线HF经过点B，点E，G分别在AB，BC上．
（1）求证：△ADE≌△CDG；
（2）若AE＝BE＝2，求BF的长．
【分析】（1）根据正方形和菱形的性质得出AD＝CD，ED＝GD，∠A＝∠C＝90°，再根据全等三角形的判定定理推出即可；
（2）过E作EQ⊥DF于Q，根据正方形的性质得出AD＝AB＝4，∠A＝90°，∠ABD＝45°，根据勾股定理求出DE和EQ，根据菱形的性质求出EF＝DE，再根据勾股定理求出QF即可．
【解答】（1）证明：∵四边形ABCD是正方形，四边形HEFG是菱形，
∴AD＝CD，ED＝GD，∠A＝∠C＝90°，
在Rt△ADE和Rt△CDG中，
，
∴Rt△ADE≌Rt△CDG（HL）；
（2）解：过E作EQ⊥DF于Q，则∠EQB＝90°，
∵四边形ABCD是正方形，
∴∠A＝90°，AD＝AB＝AE+BE＝2+2＝4，∠EBQ＝∠CBD＝45°，
∴∠QEB＝45°＝∠EBQ，
∴EQ＝BQ，
∵BE＝2，
∴2EQ2＝22，
∴EQ＝BQ＝（负数舍去），
在Rt△DAE中，由勾股定理得：DE＝＝＝2，
∵四边形EFGH是菱形，
∴EF＝DE＝2，
∴QF＝＝＝3，
∴BF＝QF﹣QB＝3﹣＝2．
【点评】本题考查了菱形的性质，全等三角形的判定，正方形的性质，勾股定理等知识点，能熟记菱形和正方形的性质是解此题的关键．
15．（2022•恩施州）如图，已知四边形ABCD是正方形，G为线段AD上任意一点，CE⊥BG于点E，DF⊥CE于点F．求证：DF＝BE+EF．
【分析】由“AAS”可证△CBE≌△DCF，可得CF＝BE，CE＝DF，可得结论．
【解答】证明：∵四边形ABCD是正方形，
∴BC＝CD，∠BCD＝90°，
∵CE⊥BG，DF⊥CE，
∴∠BEC＝∠DFC＝90°，
∴∠BCE+∠CBE＝90°＝∠BCE+∠DCF，
∴∠CBE＝∠DCF，
在△CBE和△DCF中，
，
∴△CBE≌△DCF（AAS），
∴CF＝BE，CE＝DF，
∵CE＝EF+CF，
∴DF＝BE+EF．
【点评】本题考查了正方形的性质，全等三角形的判定和性质，证明三角形全等是解题的关键．
16．（2022•雅安）如图，E，F是正方形ABCD的对角线BD上的两点，且BE＝DF．
（1）求证：△ABE≌△CDF；
（2）若AB＝3，BE＝2，求四边形AECF的面积．
【分析】（1）根据全等三角形的判定定理证明即可；
（2）根据正方形的性质，菱形的判定定理和性质定理解答即可．
【解答】（1）证明：∵四边形ABCD为正方形，
∴CD＝AB，∠ABE＝∠CDF＝45°，
又∵BE＝DF，
∴△ABE≌△CDF（SAS）．
（2）解：连接AC，交BD于点O，
∵四边形ABCD是正方形，
∴AC⊥BD，AO＝CO，DO＝BO，
又∵DF＝BE，
∴OE＝OF，AO＝CO，
∴四边形AECF是平行四边形，
∵AC⊥EF，
∴四边形AECF是菱形，
∵AB＝3，
∴AC＝BD＝6，
∵BE＝DF＝2，
∴四边形AECF的面积＝AC•EF＝×6×2＝6．
【点评】本题主要考查了全等三角形的判定和性质，正方形的性质，菱形的判定和性质，熟练掌握相关性质是解答本题的关键．
考法2：正方形判定
17．（2022•攀枝花）如图，以△ABC的三边为边在BC上方分别作等边△ACD、△ABE、△BCF．且点A在△BCF内部．给出以下结论：①四边形ADFE是平行四边形；②当∠BAC＝150°时，四边形ADFE是矩形；③当AB＝AC时，四边形ADFE是菱形；④当AB＝AC，且∠BAC＝150°时，四边形ADFE是正方形．其中正确结论有 ①②③④ （填上所有正确结论的序号）．
【分析】①利用SAS证明△EFB≌△ACB，得出EF＝AC＝AD；同理由△CDF≌△CAB，得DF＝AB＝AE；根据两边分别相等的四边形是平行四边形得出四边形ADFE是平行四边形，即可判断结论①正确；
②当∠BAC＝150°时，求出∠EAD＝90°，根据有一个角是90°的平行四边形是矩形即可判断结论②正确；
③先证明AE＝AD，根据一组邻边相等的平行四边形是菱形即可判断结论③正确；
④根据正方形的判定：既是菱形，又是矩形的四边形是正方形即可判断结论④正确．
【解答】解：①∵△ABE、△CBF是等边三角形，
∴BE＝AB，BF＝CB，∠EBA＝∠FBC＝60°；
∴∠EBF＝∠ABC＝60°﹣∠ABF；
∴△EFB≌△ACB（SAS）；
∴EF＝AC＝AD；
同理由△CDF≌△CAB，得DF＝AB＝AE；
由AE＝DF，AD＝EF即可得出四边形ADFE是平行四边形，故结论①正确；
②当∠BAC＝150°时，∠EAD＝360°﹣∠BAE﹣∠BAC﹣∠CAD＝360°﹣60°﹣150°﹣60°＝90°，
由①知四边形AEFD是平行四边形，
∴平行四边形ADFE是矩形，故结论②正确；
③由①知AB＝AE，AC＝AD，四边形AEFD是平行四边形，
∴当AB＝AC时，AE＝AD，
∴平行四边形AEFD是菱形，故结论③正确；
④综合②③的结论知：当AB＝AC，且∠BAC＝150°时，四边形AEFD既是菱形，又是矩形，
∴四边形AEFD是正方形，故结论④正确．
故答案为：①②③④．
【点评】本题考查了平行四边形及矩形、菱形、正方形的判定，等边三角形的性质，全等三角形的判定与性质，熟练掌握特殊四边形的判定方法和性质是解答此题的关键．
18．（2022•邵阳）如图，在菱形ABCD中，对角线AC，BD相交于点O，点E，F在对角线BD上，且BE＝DF，OE＝OA．
求证：四边形AECF是正方形．
【分析】先证明四边形AECF是菱形，再证明EF＝AC，即可得出结论
【解答】证明：∵四边形ABCD是菱形，
∴AC⊥BD，OA＝OC，OB＝OD，
∵BE＝DF，
∴OE＝OF，
∴四边形AECF是菱形；
∵OE＝OA＝OF，
∴OE＝OF＝OA＝OC，即EF＝AC，
∴平行四边形AECF是矩形，即∠AEC＝90°，
∴菱形AECF是正方形．
【点评】本题主要考查了菱形的性质与判定，正方形的判定，掌握相关定理是解题基础
【方法五】 成果评定法
一、单选题
1．（2023·江苏常州·统考二模）如图，把图1中边长为10的菱形沿对角线分成四个全等的直角三角形，且此菱形的一条对角线长为16，将这四个直角三角形拼成如图2所示的正方形，则图2中的阴影面积为（ ）
A．2B．4C．9D．16
【答案】B
【分析】先利用勾股定理求得此菱形的另一条对角线的长，再求得菱形的面积，进而可得阴影的面积是边长为10的正方形的面积减去菱形的面积．
【详解】解：如图1所示：
∵四边形是菱形，，
∴，
∴，
∴，
∴菱形的面积，
图2正方形的面积，
∴阴影的面积．
故选：B．
【点睛】本题考查了图形的剪拼、菱形的性质、正方形的性质，解决本题的关键是掌握菱形的性质．
2．（2023·上海崇明·统考二模）下列命题是真命题的是（ ）
A．四边都相等的四边形是正方形B．一组邻边相等的矩形是正方形
C．对角线互相垂直平分的四边形是正方形D．对角线互相垂直且相等的四边形是正方形
【答案】B
【分析】根据正方形的判定方法，逐一进行判断即可．
【详解】解：A、四边都相等的四边形是菱形，原命题是假命题，不符合题意；
B、一组邻边相等的矩形是正方形，是真命题，符合题意；
C、对角线互相垂直平分的四边形是菱形，原命题是假命题，不符合题意；
D、对角线互相垂直且相等的四边形不一定是正方形，原命题是假命题，不符合题意；
故选：B．
【点睛】本题考查判断命题的真假．熟练掌握正方形的判定方法，是解题的关键．
3．（2023·浙江台州·统考一模）如图，学校为美化校园环境，决定在一个边长为10m的正方形花坛中，按图中所示的分布方式种植郁金香和雏菊．则种植郁金香的总面积是( )
A．B．C．D．
【答案】B
【分析】如图，先确定里边四边形的形状为矩形，则郁金香的种植面积为两个等腰直角三角形的面积和矩形面积一半的和，计算解题即可．
【详解】如图，则，，
∴是平行四边形，
又∵，
∴，
∴是矩形
∴种植郁金香的总面积是，
故选B．
【点睛】本题考查矩形的判定与性质和正方形的性质，掌握矩形的的判定是解题的关键．
4．（2023·辽宁本溪·统考一模）下列命题中，是真命题的有（ ）
①对角线相等且互相平分的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相平分的四边形是平行四边形
④对角线相等的菱形是正方形
A．①②③B．①③④C．②③④D．①②④
【答案】B
【分析】直接利用矩形、菱形、平行四边形、以及正方形的判定方法分别分析进而得出答案即可．
【详解】解：①对角线相等且互相平分的四边形是矩形，故①正确；
②对角线互相平分且垂直的四边形是菱形，故②错误；
③对角线互相平分的四边形是平行四边形，故③正确；
④对角线相等的菱形是正方形，故④正确，
综上所述正确的有①③④，故B正确．
故选：B．
【点睛】本题考查了命题与定理，正确掌握特殊四边形的判定方法是解答本题的关键．
5．（2023·江苏苏州·统考二模）如图，已知正方形的边长为4，G是边中点，F在边上，且，则的长是（ ）
A．B．C．D．
【答案】A
【分析】延长至点H，使得，连接，由题意易证，则有，然后可证，则有，设，则有，最后根据勾股定理可建立方程求解．
【详解】解：延长至点H，使得，连接，如图所示：
∵四边形是边长为4的正方形，
∴，，
∴，
∴，
∴，
∵，
∴，
∴，即，
∵，
∴，
∴，
∵G是边中点，
∴，
设，则有，
∴在中，由勾股定理得：，
解得：；
故选A．
【点睛】本题主要考查全等三角形的性质与判定、正方形的性质及勾股定理，熟练掌握全等三角形的性质与判定、正方形的性质及勾股定理是解题的关键．
6．（2023·山东威海·统考一模）如图，正方形OABC的顶点A，C在坐标轴上，将正方形绕点O第1次逆时针旋转得到正方形，依此方式，连续旋转至第2023次得到正方形．若点A的坐标为，则点的坐标为（ ）
A．B．C．D．
【答案】C
【分析】根据图形可知：点在以为圆心，以为半径的圆上运动，再由旋转可知：将正方形绕点逆时针旋转后得到正方形，相当于将线段绕点逆时针旋转，可得对应点的坐标，然后发现规律是8次一循环，进而得出答案．
【详解】解：点的坐标为，
，
四边形是正方形，
，，
，
连接，如图：
由勾股定理得：，
由旋转的性质得：，
将正方形绕点逆时针旋转后得到正方形，
相当于将线段绕点逆时针旋转，依次得到，
，，，，，，，
发现是8次一循环，则，
点的坐标为；
故选：C．
【点睛】本题考查了旋转的性质、正方形的性质、坐标与图形性质、勾股定理、规律型：点的坐标等知识，解题的关键是学会从特殊到一般的探究规律的方法．
7．（2023·山东济宁·统考一模）如图，点E在正方形的对角线上，且，的两直角边分别交于点M，N．若正方形的边长为n，则重叠部分四边形的面积为（ ）
A．B．C．D．
【答案】D
【分析】如图所示，过E作于点P，于点Q，证明四边形是正方形，再证明，进而得到四边形的面积等于正方形的面积，再求出正方形的边长即可得到答案．
【详解】解：如图所示，过E作于点P，于点Q，
∵四边形是正方形，
∴，
又∵，
∴，
∴°，
∵三角形是直角三角形，
∴，
∴，
∵是的角平分线，，
∴，
∴四边形是正方形，
在和中，
，
∴
∴，
∴四边形的面积等于正方形的面积，
∵正方形的边长为n，
∴，
∵，
∴，
∴，
∴正方形的面积，
∴四边形的面积为，
故选D．
【点睛】本题主要考查了正方形的性质与判断，勾股定理，全等三角形的性质与判定，角平分线的性质，正确推出四边形的面积等于正方形的面积是解题的关键．
8．（2023·河北承德·统考一模）如图，在菱形中，、相交于点，、分别为和上的点（不与点、、重合）．其中．过点作，分别交、于点、；过点作分别交、于点、；连接、，甲、乙、丙三个同学给出了三个结论：
甲：随着长度的变化，始终成立．
乙：随着长度的变化，四边形可能为正方形．
丙：随着长度的变化，四边形的面积始终不变，都是菱形面积的一半．
下列选项正确的是（ ）
A．甲、乙、丙都对B．甲、乙对，丙不对
C．甲、丙对，乙不对D．甲不对，乙、丙对
【答案】C
【分析】连接，交于点，根据轴对称的性质得出，，，，，过点作于点，过点作于点，证明得出，即可判断甲，进而得出四边形是平行四边形，四边形是平行四边形，即可判断丙，反证法证明四边形不可能是正方形，即可求解．
【详解】如图所示，连接，交于点，
∵四边形是菱形，，，
∴
根据菱形是轴对称图形，是，的垂直平分线，
∴，，，，
∵，
∴
如图所示，过点作于点，过点作于点，
则四边形是矩形，
∴，
∵四边形是菱形，
∴
∵
∴
∴
∴，，
∴
即，故甲正确，
∵，又
∴
∴四边形是平行四边形，
∴，
∴四边形是平行四边形，
∴
∴
即四边形的面积始终不变，都是菱形面积的一半，故丙正确；
同理可得，是平行四边形，
∴
∵当是正方形时，则
∴
则四边形是正方形
∵
∴四边形不是正方形，即四边形不可能是正方形，故乙错误，
故选：C．
【点睛】本题考查了平行四边形的性质与判定，菱形的性质，正方形的性质，熟练掌握以上知识是解题的关键．
二、填空题
9．（2023·吉林长春·校考二模）一个正方形和一个直角三角形的位置如图摆放．若，则的大小为______度．
【答案】48
【分析】如图，根据邻补角可知，然后根据直角三角形的两个锐角互余及同角的余角相等可进行求解．
【详解】解：如图所示：
∵，
∴，
∵，
∴；
故答案为48．
【点睛】本题主要考查直角三角形的性质、正方形的性质及邻补角，熟练掌握直角三角形的性质、正方形的性质及邻补角是解题的关键．
10．（2023·黑龙江齐齐哈尔·统考一模）如图，正方形中，点分别在上，连接，请添加一个条件：___________，使．
【答案】（答案不唯一）
【分析】由四边形为正方形，，，添加一个条件，证明．
【详解】添加一个条件为：
∵四边形为正方形，
∴，
在与中
∴
故答案为：．
【点睛】本题考查正方形的性质和全等三角形的判定，解题的关键是根据相关性质定理，进行证明．
11．（2023·北京通州·统考一模）在中，，将一个直角尺的直角顶点O与边上的中点D重合，并绕点D旋转，分别交于点E、F，如果四边形恰巧是正方形，则的长度为__________．
【答案】2
【分析】由四边形是正方形得到，由，得到是等腰直角三角形，求出，由直角三角形的性质得到，在中，求出，即可得到答案．
【详解】解：如图，四边形是正方形，
∴，
∵，
∴是等腰直角三角形，，
∵D是边上的中点，
∴，
在中，，
∴，
∴，
故答案为：2
【点睛】此题考查了正方形的性质、勾股定理、直角三角形的性质等知识，熟练掌握相关性质是解题的关键．
12．（2023·天津西青·统考一模）如图，点是正方形中延长线上一点，连接，点是的中点，连接，若，，则的长为______．
【答案】
【分析】如图所示，过点F作分别交于G、H，则四边形为矩形，，，由正方形的性质得到，证明，得到，，在中，由勾股定理得，则，进而求出，在中，由勾股定理得．
【详解】解：如图所示，过点F作分别交于G、H，则四边形为矩形，
∴，，
∵四边形是正方形，
∴，
∵点是的中点，
∴，
又∵，
∴，
，，
在中，由勾股定理得，
∴，
∴，
∴，
在中，由勾股定理得，
故答案为：．
【点睛】本题主要考查了正方形的性质，矩形的性质与判定，勾股定理，全等三角形的性质与判定等等，正确作出辅助线构造全等三角形是解题的关键．
13．（2023·山东菏泽·统考一模）如图，四边形是边长为1的正方形，顶点A在x轴的负半轴上，顶点C在y轴的正半轴上，若直线与边有公共点，则k的取值范围是____________．
【答案】
【分析】根据正方形的性质得出点A与点B的坐标，代入解析式得出范围解答即可．
【详解】解：由题意可得：点，点，
把点A代入解析式可得：，
解得：，
把点B代入解析式可得：，
解得：，
所以k的取值范围为：，
故答案为：．
【点睛】此题考查两直线相交与平行问题，关键是根据正方形的性质得出点A与点B的坐标．
14．（2023·天津和平·统考二模）如图，已知正方形的边长为4，点为边上一点，，在的右侧，以为边作正方形，为的中点，则的长等于________．
【答案】/
【分析】以点B为坐标原点，所在直线为x轴，所在直线为y轴建立平面直角坐标系，得到点，过点G作轴于点M，则，证明，则，得到,则点G的坐标是，由为的中点，得到点H的坐标是，进一步即可求得的长．
【详解】解：以点B为坐标原点，所在直线为x轴，所在直线为y轴建立平面直角坐标系，
∵正方形的边长为4，点为边上一点，，
∴点，
过点G作轴于点M，则，
∴，
∵以为边作正方形，
∴，，
∴，
∴，
∵，
∴，
∴，
∴,
∴点G的坐标是，
∵为的中点，
∴点H的坐标是，即，
∴．
故答案为：
【点睛】此题考查了勾股定理、全等三角形的判定和性质、正方形的性质、坐标与图形等知识，数形结合和准确计算是解题的关键．
15．（2023·吉林长春·校考一模）如图，四个全等的直角三角形围成正方形和正方形，即赵爽弦图连结、，分别交、于点，已知，且，则图中阴影部分的面积之和为______ ．
【答案】//4.2
【分析】根据正方形的面积可得正方形边长的平方，设，则，根据勾股定理可得的平方的值，再根据题意可得，然后可得阴影部分的面积之和为梯形的面积．
【详解】解：，
，
设，
则，
，
，
根据题意可知：
，，
，

，
，
阴影部分的面积之和为：





．
故答案为：．
【点睛】本题考查了勾股定理的证明、全等图形、梯形的面积，首先要正确理解题意，然后会利用勾股定理和梯形的面积解题．
16．（2023·河南濮阳·统考一模）将大小不一的正方形纸片甲、乙、丙、丁放置在如图所示的长方形内（相同纸片之间不重叠），其中，若正方形“乙”的边长是m，阴影部分“戊”与阴影部分“己”的周长之差为___________．
【答案】
【分析】设正方形“甲”的边长是a，则阴影部分“戊”是长为，宽为m的矩形，阴影部分“己”的周长等同于，再求面积差即可．
【详解】解：设正方形“甲”的边长是a，则阴影部分“戊”是长为，宽为m的矩形，阴影部分“己”的周长等同于，
∴阴影部分“戊”的周长为，
∵，
∴阴影部分“戊”与阴影部分“己”的周长之差为．
故答案为：．
【点睛】本题考查正方形的性质，矩形的性质和平移的性质等知识，解题的关键是学会用 m , a 表示阴影部分“戊”与阴影部分“己”的周长解决问题．
17．（2023·天津东丽·统考一模）如图，正方形的边长为4，点是边中点，垂直平分且分别交、于点、，则的长为______.
【答案】/0.5
【分析】连接，设，则，根据线段垂直平分线的性质可得
，则.根据勾股定理列方程求出即可得的长.
【详解】
连接，设，
∵四边形是正方形，且边长为4，
，
是中点，
∵重直平分，
，
解得，
.
故答案为:
【点睛】本题主要考查了正方形的性质，线段垂直平分线的性质以及勾股定理.设未知数，根据勾股定理列方程是解题的关键.
18．（2023·辽宁葫芦岛·统考一模）如图，在中，，，点在射线上运动，连接，将沿翻折得到，交射线于，如果是直角三角形，则的长为_____________；
【答案】或
【分析】依题意分，，两种情况讨论即可求解．
【详解】解：当时，如图所示，过点作于点，则四边形是矩形，
∵折叠，
∴，
∴四边形是正方形，
∴，
∵，
∴，，，
∴，
当时，如图所示，
∵，
∴，
∵，
∴，
∴，
∵，
∴，
综上所述，的长为：或，
故答案为：或．
【点睛】本题考查了含30度角的直角三角形的性质，正方形的性质与判定，勾股定理，折叠问题，分类讨论是解题的关键．
19．（2023春·安徽宣城·九年级校联考阶段练习）如图，正方形的边长为2，G是对角线上一动点，于点E，于点F，连接．给出四种情况：①若G为上任意一点，则；②若，则；③若G为的中点，则四边形是正方形；④若，则．则其中正确的是_____．
【答案】
【分析】连接交于O，连接，先证，可得，再证，得到四边形是矩形，可得到，即可判断；
由可得，从而得出，即可判断；
先证明，可得是等腰直角三角形，得出，从而可得四边形是正方形，即可判断；
连接，在中，，求得，得到，从而得出，解得，即可求解．
【详解】解：连接交于O，连接，
∵正方形，
∴，
在和中
∴，
∴，
∵，
∴，
∴四边形是矩形，
∴，
∴，故①正确；
∵，
∴，
∴，故②正确；
∵点G为的中点，，
∴点E为的中点，
∴，
∴是等腰直角三角形，
∴，
∵四边形是矩形，
∴四边形是正方形，故③正确；
连接，
∵正方形，
∴，
在中，，
解之得：，
∴；
∵
∴，
解之得：，
∴，故④正确；
∴正确结论的序号为.
故答案为：
【点睛】本题考查了正方形的性质，等腰三角形的判定及性质，全等三角形的性质及判定，解决本题的关键是熟练掌握四边形的有关性质．
三、解答题
20．（2023·吉林长春·统考一模）如图，在中，，点D是边的中点．过点A、D分别作与的平行线，并交于点E，连结．
(1)求证：四边形是矩形．
(2)当四边形是正方形，时，______．
【答案】(1)见解析
(2)
【分析】（1）先证明四边形是平行四边形，可得，进而得到，可证得四边形是平行四边形，即可求证；
（2）根据正方形的性质和勾股定理可得，即可求解．
【详解】（1）∵，点D是中点，
∴，
∴．
∵，，
∴四边形是平行四边形，
∴．
∵，
∴．
∵，
∴四边形是平行四边形．
∵，
∴平行四边形是矩形．
（2）解：∵四边形是正方形，
∴，
∴，
∵，
∴（负值舍去），
∵，
∴．
故答案为：
【点睛】本题主要考查了矩形的判定，正方形的性质，勾股定理，熟练掌握矩形的判定，正方形的性质，勾股定理是解题的关键．
21．（2023·山东泰安·统考二模）在正方形中，E是边上一点，在延长线上取点F，使．过点F作交于点M，交于点G，交于点N．
(1)求证：；
(2)若E是的中点，请判断与的数量关系，并说明理由．
【答案】(1)见解析
(2)，理由见解析
【分析】（1）根据，以及公共角，利用即可证得；
（2）根据点E是边的中点，即有，在结合（1）的结论，可得，即可证明，则有．
【详解】（1）证明：∵四边形是正方形，，
∴，
又∵，，
∴；
（2）解：，理由如下：
如图，连接，
∵点E是边的中点，
∴，
由（1）知，
∴，
∴，
在和中，
，
∴，
∴．
【点睛】本题主要考查了正方形的性质、全等三角形的判定与性质等知识，熟练掌握全等三角形的判定定理是解题的关键．
22．（2023·山西长治·统考一模）综合与实践
问题情境：将正方形的边绕点逆时针旋转得到线段，旋转角为，连接，的平分线交直线于点．
(1)特例分析：如图1，当旋转角时，的度数为 ；
(2)深入探究：如图2，当时．
①求的度数；
②求证：．
【答案】(1)
(2)①，②证明见解析
【分析】（1）连接，根据正方形及旋转变化的性质四边形是正方形，得到，从而得出，，又根据角与角之间的关系求出，利用角平分线得，进一步证明即可求解；
（2）①连接，证明方法和同（1）相同；②由①可知是等腰直角三角形，利用勾股定理得，结合即可得出．
【详解】（1）解：如图1中，连接．
四边形是正方形，
，，
由旋转变换的性质可知，
，
，，
，，
，
，
，
，
，
平分，
，
，，
，
，，
，
，
．
故答案为：．
（2）解：①解：如图2中，连接．
四边形是正方形，
，，
由旋转变换的性质可知，
，
，，
，，
，
，
，
，
，
平分，
，
，，
，
，，
，
，
．
②证明：由①可知是等腰直角三角形，
，
，
，
．
【点睛】本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，等腰直角三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形．
23．（2023·河南周口·统考一模）综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动．
(1)操作判断
操作一：在正方形纸片的边上取一点E，沿折叠，得到折线，把纸片展平；
操作二：对折正方形纸片，使点C和点E重合，得到折线把纸片展平．
根据以上操作，判断线段的大小关系是______，位置关系是______．
(2)深入探究
如图2，设与交于点I．小华测量发现，经过思考，他连接，并作的高，尝试证明，．请你帮助完成证明过程．
(3)拓展应用
在（2）的探究中，已知正方形的边长为，当点I是的三等分点时，请直接写出的长．
【答案】(1)，
(2)见解析
(3)．
【分析】（1）作于点J，折叠的性质知是线段的垂直平分线，证明，推出即可；
（2）证明，推出，证明，推出，再证明，据此即可得到结论；
（3）设，则，，在中，利用勾股定理列式计算即可求解．
【详解】（1）解：，，理由如下，
作于点J，
由折叠的性质知是线段的垂直平分线，
∴，即，
∵四边形是正方形，
∴，，
∴四边形是矩形，
∴，，∴，
∴，
∴，
故答案为：，；
（2）解：作的高，
由折叠的性质知是线段的垂直平分线，且，
∴，
∴，
又，即，
∴，
∴，
在和中，，
∴，
∴，，
∴，
在和中，，
∴，
∴，
∴；
（3）解：设，则，
∵点I是的三等分点，
∴，，
∴，
在中，，即，
解得，
∴．
【点睛】本题考查了正方形的性质，折叠的性质，全等三角形的判定和性质，勾股定理，证明证明，是解题的关键．
24．（2023·吉林长春·校考一模）图、图均是的正方形网格，每个小正方形的边长为，每个小正方形的顶点称为格点，线段的端点均在格点上，只用无刻度的直尺，在给定的网格中，按下列要求以为边画一个平行四边形．

（1）平行四边形的面积为．
（2）图、图所画图形不全等．
（3）点、均在格点上．
【答案】见解析
【分析】根据面积确定边长，再分别作边长为的正方形、底和高都是的平行四边形即可．
【详解】解：按要求作图如下：

图①：，
以为边的正方形的面积为，
正方形即为所求；
图②：以为一边，以高作平行四边形，
四边形的面积为，
平行四边形即为所求．
【点睛】本题考查了格点作图，熟练掌握正方形和平行四边形的面积公式是解题关键．
25．（2023·安徽黄山·校考模拟预测）如图①，四边形是正方形，是等边三角形，M为对角线（不含B点）上任意一点，将绕点B逆时针旋转60°得到，连接．
(1)连接是等边三角形吗？为什么？
(2)求证：；
(3)①当M点在何处时，的值最小；
②如图②，当M点在何处时，的值最小，请你画出图形，并说明理由．
【答案】(1)是，理由见解析
(2)见解析
(3)①点M为的中点；②点M为与的交点时，的值最小，图及理由见解析
【分析】（1）根据旋转的性质可得，再根据有一个角是60°的等腰三角形是等边三角形证明即可；
（2）根据等边三角形的性质可得，再求出，然后利用“边角边”证明△AMB和△ENB全等即可；
（3）①根据两点之间线段最短可知A、M、C三点共线时，的值最小，再根据正方形的性质解答；②根据全等三角形对应边相等可得，然后求出，再根据两点之间线段最短证明．
【详解】（1）解：是等边三角形．理由如下：
如图①，∵绕点B逆时针旋转60°得到，
∴，
∴是等边三角形；
（2））证明：∵和都是等边三角形，
∴，
∴，即，
在和中，
，
∴；
（3）解：①由两点之间线段最短可知A、M、C三点共线时，的值最小，
∵四边形是正方形，
∴点M为的中点；
②当点M为与的交点时，的值最小，理由如下：
如图②，∵，
∴，
∵是等边三角形，
∴，
∴，
由两点之间线段最短可知，点E、N、M、C在同一直线上时，，
故点M为与的交点时，的值最小．
【点睛】本题考查了正方形的性质，全等三角形的判定与性质，等边三角形的判定与性质，两点之间线段最短，从两点之间线段最短考虑求解是解题的关键．
26．（2023春·江西抚州·九年级临川一中校考期中）如图，是正方形的边上一点，连接．请仅用无刻度的直尺完成画图．（保留画图痕迹，不写作法）
(1)在图（1）中，平移线段，使点与点重合；
(2)在图（2）中，将线段绕点顺时针旋转，得到线段．
【答案】(1)见解析
(2)见解析
【分析】（1）连接交于点O，作射线交于点F，连接即可；
（2）第（1）的图中，设与的交点为G，作射线交于点H，再作射线交的延长线于点M，连接即可．
【详解】（1）解：如图，线段即为所作，
；
（2）解：如图，线段即为所作，
．
【点睛】本题考查作图-旋转变换，正方形的性质，平行四边形的性质，全等三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
27．（2023·北京丰台·统考一模）在正方形中，点O为对角线的中点，点E在对角线上，连接，点F在直线上（点F与点D不重合），且．
(1)如图1，当点E在线段上（不与端点重合）时．
①求证：；
②用等式表示线段，，的数量关系并证明；
(2)如图2，当点E在线段上（不与端点重合）时，补全图形，并直接写出线段，，的数量关系．
【答案】(1)①见解析；②，证明见解析；
(2)图见解析，．
【分析】（1）连接，证明，，可得，，，从而可得答案；②过点E作交于点G，证明，，再证明，可得 ，从而可得结论；
（2）先补全图形，过点E作于N，交于M，证明，可得，由线段的和差关系可求解．
【详解】（1）①证明：连接．
四边形是正方形
，．
点E在对角线上
，
．
，．
，
．
．
②；
证明：过点E作交于点G．
，
．
，，
，
，
，，
，
．
．
（2）补全图形如下：
如图2，过点E作于N，交于M，
∵四边形是正方形，
∴，，，
∵，
∴四边形是矩形，是等腰直角三角形，
∴，，，，
∴，
又∵，
∴，
∴，
∵，
∴．
即．
【点睛】本题是四边形综合题目，考查了正方形的性质，全等三角形的判定与性质，等腰直角三角形的性质，勾股定理的应用，本题综合性强，熟练掌握正方形的性质和等腰直角三角形的判定与性质，证明三角形全等是解题的关键，属于中考常考题型．
28．（2023·河南南阳·统考一模）综合与实践
数学活动课上，同学们开展了以折叠为主题的探究活动，如图1．已知矩形纸片，其中，．
(1)操作判断
将矩形纸片按图1折叠，使点落在边上的点处，可得到一个的角，请你写出一个的角．
(2)探究发现
将图1的纸片展平，把四边形剪下来如图2，取边的中点，将沿折叠得到，延长交于点，判断的周长是否为定值，若是，求出该定值；若不是，请说明理由．
(3)拓展应用
改变图2中点的位置，令点为射线上一动点，按照（2）中方式将沿折叠得到，所在直线交于点，若点为的三分点，请直接写出此时的长．
【答案】(1)（或，，）
(2)是定值，
(3)或
【分析】（1）利用矩形的性质和折叠的性质证明四边形是正方形，然后利用正方形的性质即可得出结论；
（2）周长为定值．连结，先证明四边形是矩形，可得，，由折叠性质并结合为的中点可得到，，，然后证明可得到，最后计算可知是一常数，结论得证；
（3）分两种情况计算：①当点为的三分点且靠近点时，②当点为的三分点且靠近点时，利用勾股定理和折叠的性质即可得出结论．
【详解】（1）解：∵四边形是矩形，
∴，
∵将矩形纸片按图1折叠，使点落在边上的点处，
∴，，
∴，
∴四边形是矩形，
∵，
∴四边形是正方形，
∴，
∴的角有（或，，）．
（2）周长为定值．
解：连结，
∵四边形是矩形，，，
，，
∵四边形是正方形，
∴，，
∴，
∴四边形是矩形，
∴，，
由折叠性质得：，，，
∵为的中点，
∴，
∴，
在与中，
，
∴
∴，
∴的周长为：
，
即：的周长为定值．
（3）①如图，当点为的三分点且靠近点时，连接，
∴，
∴，
在中，，
∴；
②如图，当点为的三分点且靠近点时，连接，
∴，
在中，，
∴；
综上所述，的长为或．
【点睛】本题是四边形综合题，主要考查折叠的性质，矩形的判定和性质，正方形的判定与性质，全等三角形的判定与性质，勾股定理等知识，运用了分类讨论的思想．通过添加适当辅助线构造全等三角形是解题的关键．
29．（2023·北京门头沟·统考一模）已知正方形和一动点E，连接，将线段绕点C顺时针旋转得到线段，连接，．
(1)如图1，当点E在正方形内部时，
①依题意补全图1；
②求证：；
(2)如图2，当点E在正方形外部时，连接，取中点M，连接，，用等式表示线段与的数量关系，并证明．
【答案】(1)①见解析；②见解析
(2)；理由见解析
【分析】（1）①根据题意补全图形即可；
②证明，根据全等三角形对应边相等得出结果即可；
（2）连接、，延长，使，连接，延长交于点G，证明，得出，，证明，得出，，证明，得出，即可证明结论．
【详解】（1）解：①依题意补全图1，如图所示：
②∵四边形为正方形，
∴，，
根据旋转可知，，，
∴，
∴，
∴，
∴；
（2）解：；理由如下：
连接、，延长，使，连接，延长交于点G，如图所示：
∵四边形为正方形，
∴，，
根据旋转可知，，，
∴，
∴，
∴，
∴，，
∵，
，
∴，
∵点M为的中点，
∴，
∵，，
∴，
∴，，
∴，
∴，
∵，
∴，
∵，，
∴，
∵，
∴，
∴，
∵，
∴．
【点睛】本题主要考查了全等三角形的判定和性质，正方形的性质，旋转的性质，平行线的判定和性质，解题的 关键是作出辅助线，构造全等三角形，熟练掌握三角形全等的判定方法．
30．（2023·河南安阳·统考二模）综合与实践综合与实践课上，老师与同学们以“特殊的三角形”为主题开展数学活动．
(1)操作判断：如图1，在中，，点P是直线上一动点．操作一：连接，将线段绕点P逆时针旋转得到，连接，如图2．根据以上操作，判断：如图3，当点P与点A重合时，则四边形的形状是 ；
(2)迁移探究：①如图4，当点P与点C重合时，连接，判断四边形的形状，并说明理由；
②当点P与点A，点C都不重合时，试猜想与的位置关系，并利用图2证明你的猜想；
(3)拓展应用：当点P与点A，点C都不重合时，若，请直接写出的长．
【答案】(1)正方形
(2)①四边形是平行四边形，见解析；②，见解析
(3)的长为或
【分析】由旋转得，，而，，则，，所以，即可证明四边形是正方形，于是得到问题的答案；
因为点与点重合，所以，，则，即可证明四边形是平行四边形；
作交于点，连接，则，可证明，得，，则，，得，即可证明四边形是矩形，则；
分两种情况，一是点在线段上，作交于点，连接，则，，四边形是矩形，因为，所以；二是点在线段的延长线上，作交的延长线于点，连接，可证明，得，，则，，进而证明四边形是矩形，因为，所以．
【详解】（1）解：由旋转得，，
点与点重合，
，，
，，
，，
则，
四边形是平行四边形，
，，
四边形是正方形，
故答案为：正方形．
（2）解：①四边形是平行四边形，
证明：点与点重合，
，，
则，
四边形是平行四边形．
，
证明：如图，作交于点，连接，则，
，
，，
，
，
，
，
∴，
，，
，，
则，
四边形是平行四边形，
，
四边形是矩形，
，
．
（3）解：当点在线段上，如图，作交于点，连接，则，
由得，四边形是矩形，
，，
，
，
；
当点在线段的延长线上，如图，作交的延长线于点，连接，
，
，
，
，
，
，
∴，
，，
，，
，
，
四边形是平行四边形，
，
四边形是矩形，
，
，
综上所述，的长为或．
【点睛】本题重点考查等腰直角三角形的性质、全等三角形的判定与性质、旋转的性质、正方形的判定、平行四边形的判定、矩形的判定与性质、勾股定理、数形结合与分类讨论数学思想的运用等知识与方法，此题综合性强，难度较大，属于考试压轴题．