






苏科版(2024)九年级上册2.5 直线与圆的位置关系精品ppt课件
展开1.理解直线与圆的三种位置关系;
2.会利用圆心到直线的距离d与圆的半径r之间的数量关系判别直线与圆的位置关系.
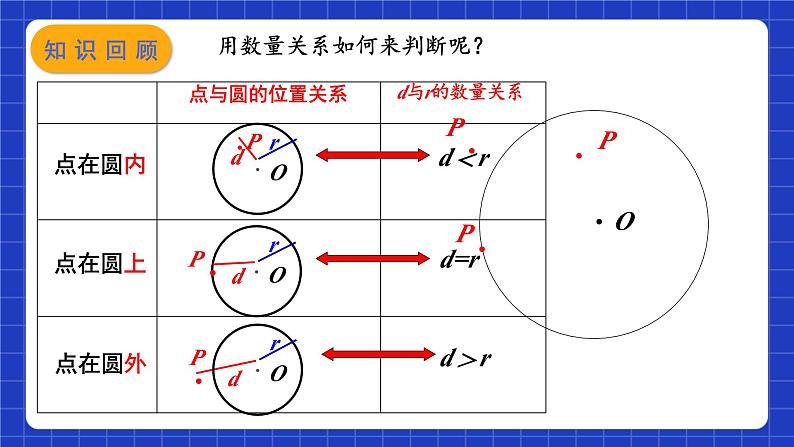
点和圆的位置关系有几种?
用数量关系如何来判断呢?
如果把太阳看作一个圆,把地平线看作一条直线,那么通过上面的视频请你类比点与圆的位置关系,猜想直线与圆的位置关系有几种?
操作1.在纸上画一条直线,并在纸上上下移动一枚硬币.
操作2.在纸上画一个圆,并在纸上上下移动透明直尺.
观察两次操作,如果将硬币看作圆,直尺的边缘看作直线,随着硬币或直尺的移动,直线与圆的位置关系发生怎样的变化?
思考1.在直线与圆的不同位置关系中,公共点个数有变化吗?
直线与圆有两个公共点时,叫做直线和圆相交.
直线与圆有唯一公共点时,叫做直线和圆相切.
直线与圆没有公共点时,叫做直线与圆相离.
思考2.在直线与圆的不同位置关系中,圆心到直线的距离有变化吗?
思考3.它与圆的半径的大小有什么关系吗?
类比点和圆的位置关系,直线和圆的位置关系是否也可以用d与r数量关系来刻画呢?
(1)与圆有公共点的直线是圆的切线 ( )(2)过圆外一点画一条直线,则直线与圆相离 ( )(3)过圆内一点画一条直线,则直线与圆相交 ( )
2.已知圆的直径为12cm,设直线和圆心的距离为d :
(3)若d=8cm ,则直线与圆______, 直线与圆有____个公共点.
(2)若d=6cm ,则直线与圆______, 直线与圆有____个公共点.
(1)若d=4cm ,则直线与圆______, 直线与圆有____个公共点.
(3)若AB和⊙O相交,则 .
3.已知⊙O的半径为3cm, 圆心O与直线AB的距离为d, 根据条件 填写d的范围: (1)若AB和⊙O相离, 则 ; (2)若AB和⊙O相切, 则 ;
解:过O作OD⊥AB,垂足为D.
∴∠AOD=∠A =45°,
又∵OD2+ AD2 = AO2 ,AO=4,
(1)当r=2时, d >r,AB所在直线与⊙O相离.
(3)当r=3时, d<r,AB所在直线与⊙O相交.
例2. 已知:如图示,∠AOB=30°,M为OB上一点,以M为圆心,5cm长为半径作圆,若M在OB上运动,问:①当OM满足___________时,⊙M与OA相离?②当OM满足___________时,⊙M与OA相切?③当OM满足___________时,⊙M与OA相交?
1.在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,以点C为圆心,r为半径的圆与直线AB有怎样的位置关系? (1)r=2 cm; (2)r=2.4 cm; (3)r=3 cm.
解:(1)直线AB与⊙C相离. (2)直线AB与⊙C相切. (3)直线AB与⊙C相交.
解:如图,过O点作OD⊥BC,垂足为D∵∠C=90°,∠A=60°∴∠B=30°,∴OB=2OD当0<OD<1,即0<OB<2时,⊙O分别与直线BC相交.当OD=1,即OB=2时,⊙O分别与直线BC相切.当OD>1,即2<OB<5时,⊙O分别与直线BC相离.
2.如图,Rt△ABC中,∠C=90°,∠A=60°,AB=5,且⊙O的半径为1,圆心O在AB什么位置时,⊙O分别与直线BC相交、相离、相切?
3.已知⊙O的半径r=7cm,直线l1 // l2,且l1与⊙O相切,圆心O到l2的距离为9cm,求l1与l2的距离.
解:(1) l2与l1在圆的同一侧: m=9-7=2 (cm)
(2) l2与l1在圆的两侧: m=9+7=16 (cm)
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由_____________________的个数来判断;
在实际应用中,常采用第二种方法判定.
圆心到直线的距离d与半径r
(2)根据性质,由___________________________的关系来判断.
先作垂直,求出距离并与半径的比较得到.
特别提醒:在图中没有d要先做出该垂线段
相离:0个相切:1个相交:2个
相离:d>r相切:d=r相交:d
d>r:相离d=r:相切d
2.如果直线l与☉O有公共点,那么直线l与☉O的位置关系是( )
A.相交 B.相切 C.相离 D.相切或相交
3.☉O的半径r为5cm,点P到圆心O的距离为5cm,过点P画直线l,则直线l与☉O的公共点有( )
A.3个 B.1个 C.2个 D.1个或2个
4. 如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则☉C的半径为( )
5.已知⊙O的半径为3cm,点P在直线l上,点P到⊙O的圆心O的距离为3cm,则l与⊙O的位置关系为( ).A.相交 B.相切 C.相离D.相交或相切
6.已知⊙O的直径为8cm,点O到直线的距离为d:(1)若直线与⊙O相切,则d=____;(2)若d=3cm,则直线与⊙O有_____个公共点; (3)若d=5cm,则直线与⊙O的位置关系是____.
7.如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为___________
8. 如图,AB是半径为6cm的☉O的弦,AB=6cm.以点O为圆心,3cm长为半径的圆与AB所在直线有怎样的位置关系?请说明理由.
. A (-3,-4)
①已知⊙A的直径为6,点A的坐标为(-3,-4),则x轴与⊙A的位置关系是_____, y轴与⊙A的位置关系是_____.
②若⊙A要与x轴相切,则⊙A该向上移动多少个单位?
若⊙A要与x轴相交呢?
大于1个单位而小于7个单位
③在平面直角坐标系中有一点A(-3,-4),以点A为圆心,r长为半径时,思考:随着r的变化,⊙A与坐标轴交点的变化情况.
(1)当r<3时,圆A与坐标轴有0个公共点;(2)当r=3时,圆A与坐标轴有1个公共点;(3)当3<r<4时,圆A与坐标轴有2个公共点;(4)当r=4时,圆A与坐标轴有3个公共点;(5)当4<r<5时,圆A与坐标轴有4个公共点;(6)当r=5时,圆A与坐标轴有3个公共点;(7)当r>5时,圆A与坐标轴有4个公共点.
苏科版(2024)九年级上册第2章 对称图形——圆2.5 直线与圆的位置关系一等奖ppt课件: 这是一份苏科版(2024)九年级上册<a href="/sx/tb_c17322_t3/?tag_id=26" target="_blank">第2章 对称图形——圆2.5 直线与圆的位置关系一等奖ppt课件</a>,共31页。PPT课件主要包含了学习目标,有且只有一条,知识回顾,操作与观察,切线长概念,不可度量,新知归纳,相等度量或者翻折,猜想与探索,切线长定理等内容,欢迎下载使用。
苏科版(2024)九年级上册第2章 对称图形——圆2.5 直线与圆的位置关系评优课ppt课件: 这是一份苏科版(2024)九年级上册<a href="/sx/tb_c17322_t3/?tag_id=26" target="_blank">第2章 对称图形——圆2.5 直线与圆的位置关系评优课ppt课件</a>,共37页。PPT课件主要包含了学习目标,生活情境,操作与思考,∠B∠C,有且只有一个,新知归纳,新知巩固,三角形内心的性质,三角形角平分线,到三边的距离等内容,欢迎下载使用。
苏科版(2024)九年级上册第2章 对称图形——圆2.5 直线与圆的位置关系一等奖ppt课件: 这是一份苏科版(2024)九年级上册<a href="/sx/tb_c17322_t3/?tag_id=26" target="_blank">第2章 对称图形——圆2.5 直线与圆的位置关系一等奖ppt课件</a>,共40页。PPT课件主要包含了学习目标,d<r,d=r,d>r,知识回顾,生活情境,操作与思考,切线的判定定理,∵OD为⊙O的半径,符号语言等内容,欢迎下载使用。













