2025高考数学总复习专项复习（讲义）--概率专题三（含解析）

这是一份2025高考数学总复习专项复习（讲义）--概率专题三（含解析），共21页。学案主要包含了注意基础知识的整合，查漏补缺，保强攻弱，提高运算能力，规范解答过程，强化数学思维，构建知识体系，解题快慢结合，改错反思，重视和加强选择题的训练和研究等内容，欢迎下载使用。
一、注意基础知识的整合、巩固。进一步夯实基础，提高解题的准确性和速度。
二、查漏补缺，保强攻弱。针对“一模”的问题要根据自己的实际情况作出合理的安排。
三、提高运算能力，规范解答过程。一定要重视运算技巧粗中有细，提高运算准确性和速度。
四、强化数学思维，构建知识体系。同学们在听课时注意把重点要放到理解老师对问题思路的分析以及解法的归纳总结，以便于同学们在刷题时做到思路清晰，迅速准确。
五、解题快慢结合，改错反思。要适当地选择好的方案，解题动作要快要自信。
六、重视和加强选择题的训练和研究。对于选择题不但要答案正确，还要优化解题过程，提高速度。灵活运用特值法、排除法、数形结合法、估算法等。
人教A版数学--概率专题三
知识点一 独立性检验解决实际问题,计算条件概率
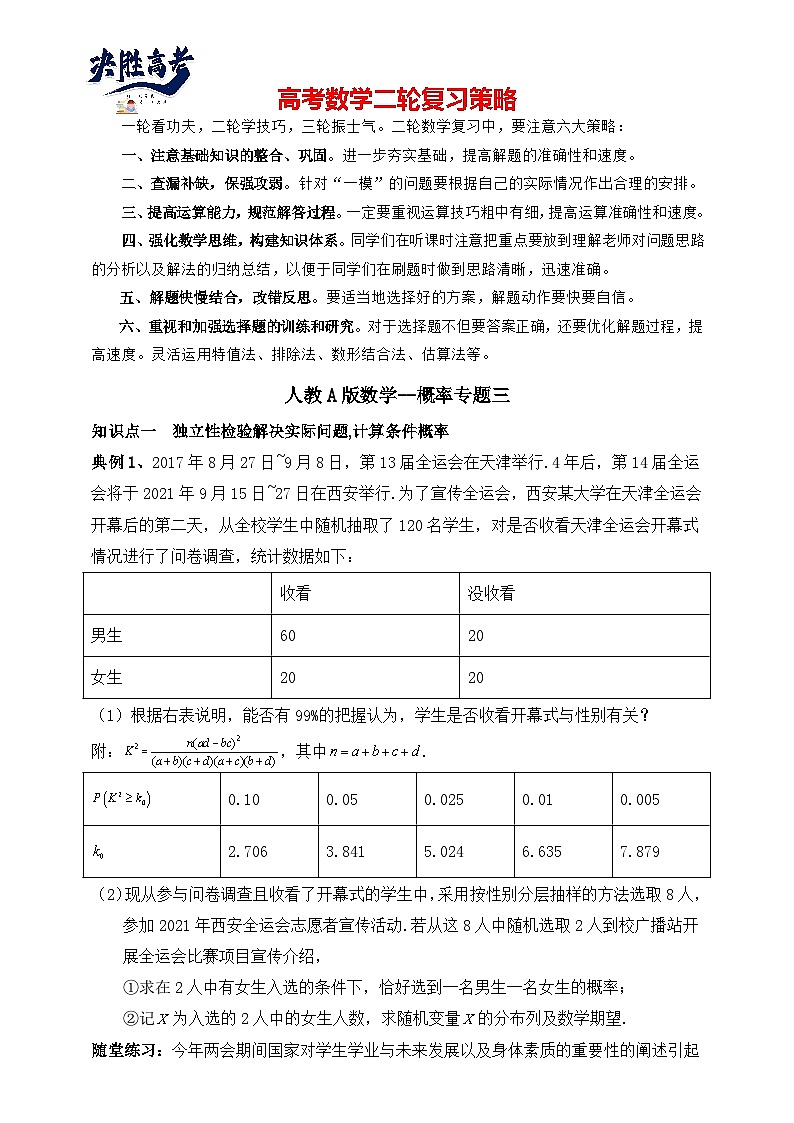
典例1、2017年8月27日~9月8日，第13届全运会在天津举行.4年后，第14届全运会将于2021年9月15日~27日在西安举行.为了宣传全运会，西安某大学在天津全运会开幕后的第二天，从全校学生中随机抽取了120名学生，对是否收看天津全运会开幕式情况进行了问卷调查，统计数据如下：
（1）根据右表说明，能否有99%的把握认为，学生是否收看开幕式与性别有关？
附：，其中.
（2）现从参与问卷调查且收看了开幕式的学生中，采用按性别分层抽样的方法选取8人，参加2021年西安全运会志愿者宣传活动.若从这8人中随机选取2人到校广播站开展全运会比赛项目宣传介绍，
①求在2人中有女生入选的条件下，恰好选到一名男生一名女生的概率；
②记为入选的2人中的女生人数，求随机变量的分布列及数学期望.
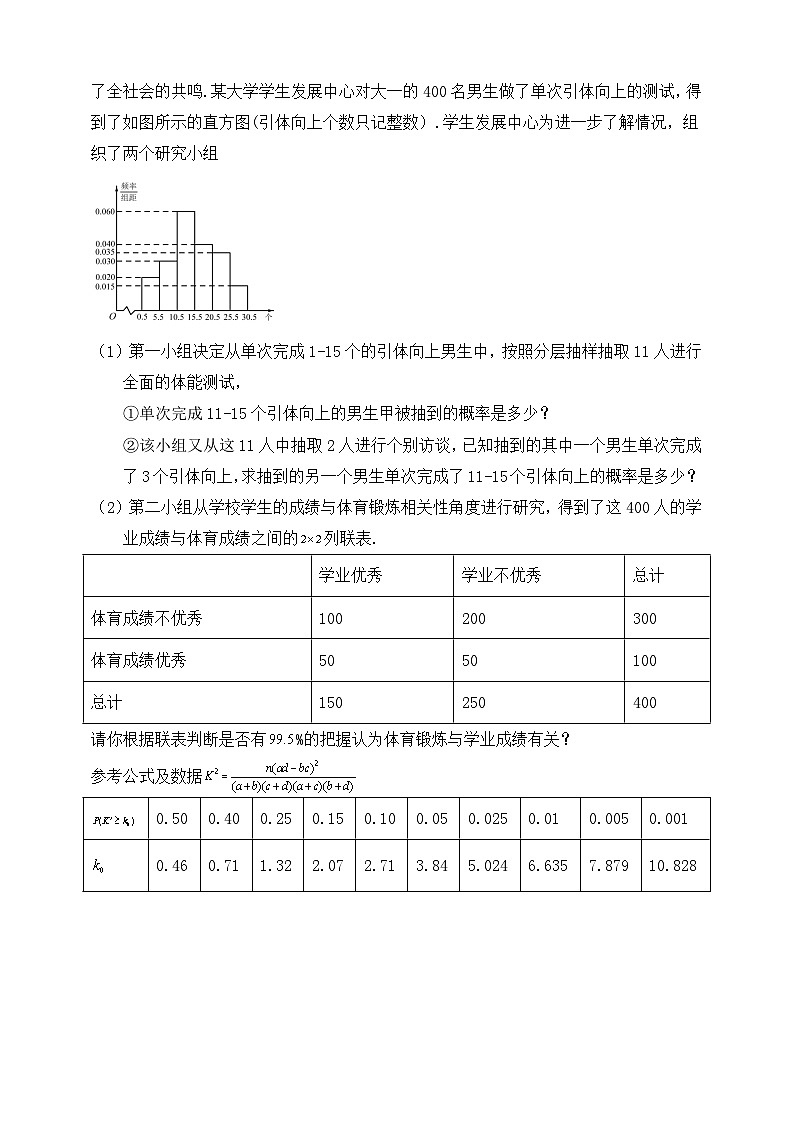
随堂练习：今年两会期间国家对学生学业与未来发展以及身体素质的重要性的阐述引起了全社会的共鸣.某大学学生发展中心对大一的400名男生做了单次引体向上的测试，得到了如图所示的直方图(引体向上个数只记整数）.学生发展中心为进一步了解情况，组织了两个研究小组
（1）第一小组决定从单次完成1-15个的引体向上男生中，按照分层抽样抽取11人进行全面的体能测试，
①单次完成11-15个引体向上的男生甲被抽到的概率是多少？
②该小组又从这11人中抽取2人进行个别访谈，已知抽到的其中一个男生单次完成了3个引体向上，求抽到的另一个男生单次完成了11-15个引体向上的概率是多少？
（2）第二小组从学校学生的成绩与体育锻炼相关性角度进行研究，得到了这400人的学业成绩与体育成绩之间的列联表.
请你根据联表判断是否有%的把握认为体育锻炼与学业成绩有关？
参考公式及数据
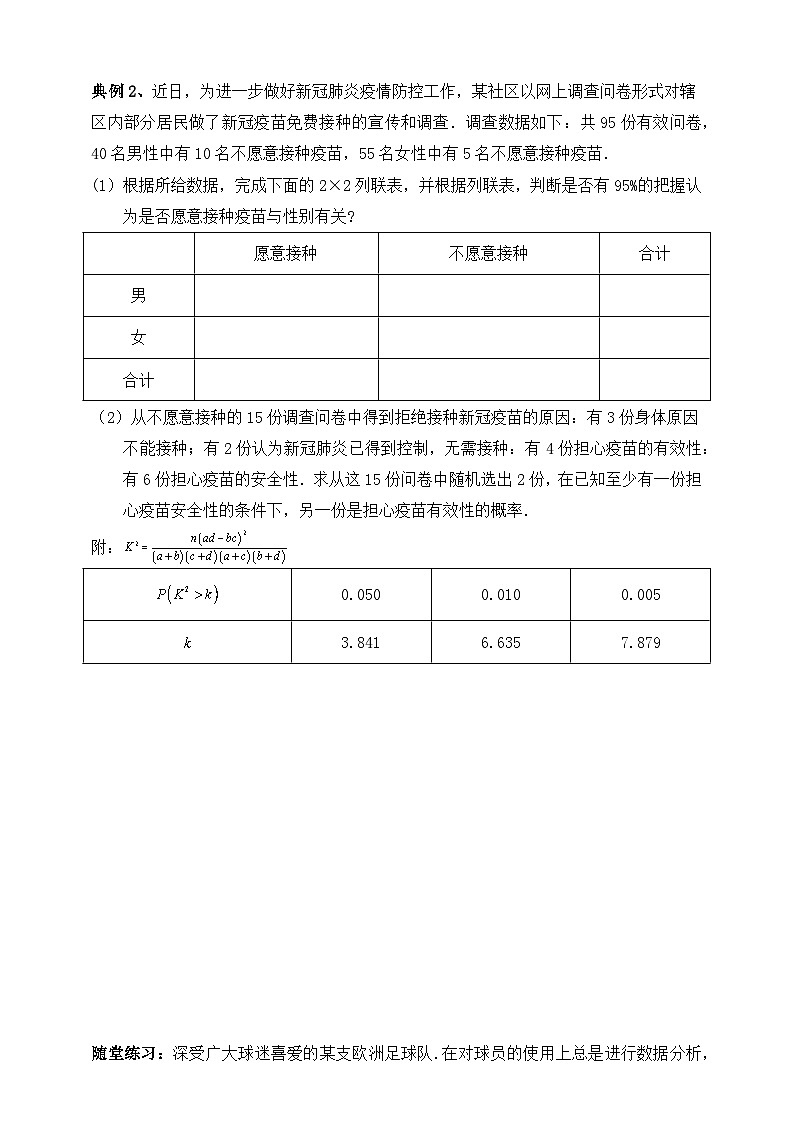
典例2、近日，为进一步做好新冠肺炎疫情防控工作，某社区以网上调查问卷形式对辖区内部分居民做了新冠疫苗免费接种的宣传和调查．调查数据如下：共95份有效问卷，40名男性中有10名不愿意接种疫苗，55名女性中有5名不愿意接种疫苗．
(1）根据所给数据，完成下面的2×2列联表，并根据列联表，判断是否有95%的把握认为是否愿意接种疫苗与性别有关?
（2）从不愿意接种的15份调查问卷中得到拒绝接种新冠疫苗的原因：有3份身体原因不能接种；有2份认为新冠肺炎已得到控制，无需接种：有4份担心疫苗的有效性：有6份担心疫苗的安全性．求从这15份问卷中随机选出2份，在已知至少有一份担心疫苗安全性的条件下，另一份是担心疫苗有效性的概率．
附：
随堂练习：深受广大球迷喜爱的某支欧洲足球队.在对球员的使用上总是进行数据分析，为了考查甲球员对球队的贡献，现作如下数据统计：
（1）求、、、、的值，据此能否有的把握认为球队胜利与甲球员参赛有关；
（2）根据以往的数据统计，乙球员能够胜任前锋、中锋、后卫以及守门员四个位置，且出场率分别为：、、、，当出任前锋、中锋、后卫以及守门员时，球队输球的概率依次为：、、、.则：
①当他参加比赛时，求球队某场比赛输球的概率；
②当他参加比赛时，在球队输了某场比赛的条件下，求乙球员担当前锋的概率；
③如果你是教练员，应用概率统计有关知识，该如何使用乙球员？
附表及公式：
.
典例3、2021年6月2日巴蜀中学成功地举办了一年一度的大型学生社团文化节，吸引了众多学生．巴蜀中学目前共有社团近40个，由高一和高二学生组成，参加社团的学生共有四百人左右．已知巴蜀中学高一和高二的所有学生中男生与女生人数比为6：4，为了解学生参加社团活动的情况，按性别采用分层抽样的方法抽取部分学生，统计得到如下等高累积型条形图：
（1）求巴蜀中学参加社团的学生中，任选1人是男生的概率；
（2）若抽取了100名学生，完成下列列联表，并依据小概率值的独立性检验，能否认为巴蜀中学高一和高二学生的性别与参加学生社团有关联？请说明理由．
附：，
临界值表：
随堂练习：一家大型超市委托某机构调查该超市的顾客使用移动支付的情况．调查人员从年龄在[20，60]内的顾客中，随机抽取了200人，调查结果如图：
（1）为推广移动支付，超市准备对使用移动支付的每位顾客赠送1个环保购物袋．若某日该超市预计有10000人购物，试根据上述数据估计，该超市当天应准备多少个环保购物袋？
（2）填写下面列联表，并根据列联表判断是否有99.9%的把握认为使用移动支付与年龄有关：
（3）现从该超市年龄在20到60的200人的顾客中，随机依次抽取2人，已知第1次抽到的是使用移动支付的顾客，求第2次抽到的是不使用移动支付的顾客的概率．
附表：
．
知识点二 根据频率分布表解决实际问题,用频率估计概率,求离散型随机变量的均值
典例4、某地区为了实现产业的转型发展，利用当地旅游资源丰富多样的特点，决定大力发展旅游产业，一方面对现有旅游资源进行升级改造，另一方面不断提高旅游服务水平．为此该地区旅游部门，对所推出的报团游和自助游项目进行了深入调查，如表是该部门从去年某月到该地区旅游的游客中，随机抽取的100位游客的满意度调查表．
（1）由表中的数据分析，老年人、中年人和青年人这三种人群中，哪一类人群更倾向于选择报团游？
（2）为了提高服务水平，该旅游部门要从上述样本里满意度为“不满意”的游客中，随机抽取3人征集整改建议，记表示这3人中老年人的人数，求的分布列和期望；
（3）若你朋友要到该地区旅游，根据表中的数据，你会建议他选择哪种旅游项目？
随堂练习：某快递公司收取快递费用的标准是：重量不超过的包裹收费元；重量超过的包裹，除收费元之外，超过的部分，每超出 (不足，按计算)需再收元.该公司将最近承揽的件包裹的重量统计如表：
公司对近天，每天揽件数量统计如表：
以上数据已做近似处理，并将频率视为概率.
（）计算该公司未来天揽件数在之间的概率；
（）①估计该公司对每件包裹收取的快递费的平均值；
②公司将快递费的三分之一作为前台工作人员的工资和公司利润，剩余的用作其他费用.目前前台有工作人员人，每人每天揽件不会超过件，且日工资为元.公司正在考虑是否将前台工作人员裁减人，试计算裁员前后公司每日利润的数学期望，并判断裁员是否对提高公司利润更有利?
典例5、北京市某区针对高三年级的一次测试做调研分析，随机抽取同时选考物理､化学的学生330名，下表是物理､化学成绩等级和人数的数据分布情况：
（1）从该区高三年级同时选考物理､化学的学生中随机抽取1人，已知该生的物理成绩等级为，估计该生的化学成绩等级为的概率；
（2）从该区高三年级同时选考物理､化学的学生中随机抽取2人，以表示这2人中物理､化学成绩等级均为的人数，求的分布列和数学期望（以上表中物理､化学成绩等级均为的频率作为每名学生物理､化学成绩等级均为的概率）；
（3）记抽取的330名学生在这次考试中数学成绩（满分150分）的方差为，排名前的成绩方差为，排名后的成绩方差为，则不可能同时大于和，这种判断是否正确.（直接写出结论）.
随堂练习：自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况，随机抽取了100人，统计结果整理如下：
（1）现随机抽取 1 名顾客，试估计该顾客年龄在且未使用自由购的概率；
（2）从被抽取的年龄在使用自由购的顾客中，随机抽取3人进一步了解情况，用表示这3人中年龄在的人数，求随机变量的分布列及数学期望；
（3）为鼓励顾客使用自由购，该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物，试估计该超市当天至少应准备多少个环保购物袋.
典例6、2021年是北京城市轨道交通新线开通的“大年”，开通线路的条､段数为历年最多.12月31日首班车起，地铁19号线一期开通试运营.地铁19号线一期全长约22公里，共设10座车站，此次开通牡丹园､积水潭､牛街､草桥､新发地､新宫共6座车站.在试运营期间，地铁公司随机选取了乘坐19号线一期的名乘客，记录了他们的乘车情况，得到下表（单位：人）：
（1）在试运营期间，从在积水潭站上车的乘客中任选一人，估计该乘客在牛街站下车的概率；
（2）在试运营期间，从在积水潭站上车的所有乘客中随机选取三人，设其中在牛街站下车的人数为，求随机变量的分布列以及数学期望；
（3）为了研究各站客流量的相关情况，用表示所有在积水潭站上下车的乘客的上､下车情况，“”表示上车，“”表示下车.相应地，用，分别表示在牛街，草桥站上､下车情况，直接写出方差，，大小关系.
随堂练习：2022年冬奥会在北京举行，冬奥会吉祥物“冰墩墩”自亮相以来就好评不断，出现了“一墩难求”的现象.主办方现委托某公司推出一款以“冰墩墩”为原型的纪念品在专卖店进行售卖.已知这款纪念品的生产成本为80元/件，为了确定其销售价格，调查了对这款纪念品有购买意向的消费者（以下把对该纪念品有购买意向的消费者简称为消费者）的心理价位，并将收集的100名消费者的心理价位整理如下：
假设当且仅当这款纪念品的销售价格小于或等于某位消费者的心理价位时，该消费者就会购买该纪念品.公司为了满足更多消费者的需求，规定每位消费者最多只能购买一件该纪念品.设这款纪念品的销售价格为x（单位：元/件），，且每位消费者是否购买该纪念品相互独立.用样本的频率分布估计总体的分布，频率视为概率.
（1）若，试估计消费者购买该纪念品的概率；
（2）在（1）的前提下，某时段有4名消费者进店，X为这一时段该纪念品的购买人数，试求X的分布列和数学期望；
（3）假设共有M名消费者，设该公司售卖这款纪念品所得总利润为Y（单位：元），当该纪念品的销售价格x定为多少时，Y的数学期望达到最大值？
人教A版数学--概率专题三答案
典例1、答案：(1) 有99%的把握认为，收看开幕式与性别有关；（2）①；②答案见解析.
解：（1）因为，
所以有99%的把握认为，收看开幕式与性别有关.
（2）①根据分层抽样方法得，选取的8人中，男生人，女生人，
记事件“选出的两人中有女生”，共有或种不同的选法，
“选出的两人为一名男生､一名女生”，共有种不同的选法，
则
②根据题意，所有可能取值为
所以的分布列为
(或服从超几何分布，，，，.)
随堂练习：答案：（1）①② （2）有
解:（1）①因为0.02：0.03：0.06＝2：3：6， 所以 ，，
则从1～5，6～10，11～15中选出的个数分别为2个，3个，6个，
因为单次完成11～15个引体向上的人数共有0.06×5×400＝120人，
则单次完成11～15个引体向上的男生甲被抽到的概率是p＝
②由题知抽到的另一个男生单次完成了11-15个引体向上的概率是
（2）因为K2= ≈8.889＞7.879，
所以有99.5%的把握认为体育锻炼与学业成绩有关．
典例2、答案：（1）列联表见解析；有；（2）．
解:（1）
有的把握认为是否愿意接种疫苗与性别有关．
（2）设事件A为至少有一份担心疫苗安全性，事件B为另一份担心疫苗有效性，
则,, 所以.
随堂练习：答案：（1），，，有的把握认为球队胜利与甲球员参赛有关
（2）①；②；③多让乙球员担当守门员，来扩大赢球场次
解：（1）由列联表中的数据可得，，，
，
有的把握认为球队胜利与甲球员参赛有关.
（2）①设表示“乙球员担当前锋”；表示“乙球员担当中锋 ”；
表示“乙球员担当后卫”； 表示“乙球员担当守门员”；表示“球队输掉某场比赛”，
则
；
②；
③因为，
， ，
所以，，
所以应该多让乙球员担当守门员，来扩大赢球场次.
典例3、答案：（1）：（2）填表见解析；性别与参加社团无关；答案见解析．
解:（1）方法（1）：设高一和高二的所有学生中任选一人是男生、是女生分别为事件、
设高一和高二的所有学生中任选一人参加社团为事件
则， 则．
方法（2）：用第（2）问的列联表中的条件频数直接求解
设高一和高二的所有学生中任选一人是男生为事件
设高一和高二的所有学生中任选一人参加社团为事件 则．
（2）列联表如下：
零假设为：性别与参加社团独立，即性别与参加社团无关．
根据列联表中的数据，经计算得到：，
依据小概率值的独立性检验，没有充分的证据推断不成立，
因此可以认为成立，即性别与参加社团无关．
随堂练习：答案：（1）个；（2）填表见解析；有99.9%的把握认为使用移动支付与年龄有关；（3）．
解：（1）根据图中数据，得到如下表格：
由频率估计概率，计算得该超市使用移动支付的概率为：；
所以某日该超市预计当天应准备环保购物袋的个数为： ；
（2）填写下面列联表，并根据列联表判断是否有99.9%的把握认为使用移动支付与年龄有关：
假设移动支付与年龄无关，则K2的观测值，
因为56.17>10.828， 所以有99.9%的把握认为使用移动支付与年龄有关；
（3）解法一：记事件A：第1次抽到的是使用移动支付的顾客，
事件B：第2次抽到的是不使用移动支付的顾客， 所以；
解法二：记事件A：第1次抽到的是使用移动支付的顾客，
事件B：第2次抽到的是不使用移动支付的顾客，
则 所以
典例4、答案：（1）老年人更倾向于选择报团游；（2）分布列见解析，；（3）建议他选择报团游．
解：（1）由表中数据可得老年人、中年人和青年人选择报团游的频率分别为
，，，
因为，所以老年人更倾向于选择报团游；
（2）由题意可得，的可能取值为0，1，2，
所以， ， ，
所以的分布列为：
所以；
（3）由上表可知，报团游的满意率为， 自助游的满意率为，
因为，故建议他选择报团游．
随堂练习：答案：（1）；（2）①元；②裁员前期望值为1000元，裁员后期望值为元，不利.
解:（）样本包裹件数在之间的天数为，频率，
显然未来天中，包裹件数在之间的概率为
（）（）样本中快递费用及包裹件数如下表：
故样本中每件快递收取的费用的平均值为（元），
故该公司对每件快递收取的费用的平均值可估计为元
（）根据题意及（）（），揽件数每增加，可使前台工资和公司利润增加（元），
将题目中的天数转化为频率，得
若不裁员，则每天可揽件的上限为件，公司每日揽件数情况如下：
故公司平均每日利润的期望值为（元）；
若裁员人，则每天可揽件的上限为件，公司每日揽件数情况如下：
故公司平均每日利润的期望值为（元）
因，故公司将前台工作人员裁员人对提高公司利润不利.
典例5、答案： （1） （2）分布列答案见解析，数学期望为 （3）不正确
解：（1）设事件为“该生物理成绩等级为的情况下，化学成绩等级为”，
样本中物理成绩等级为的人数为，在该群体中化学成绩等级为的人数为110，所以频率为，由样本估计总体可得，
故该生物理成绩等级为，估计该生化学成绩等级为的概率为.
（2）从该区高三年级同时选考物理､化学的学生随机选取一名，
物理､化学成绩等级均为的概率估计为.
由题意随机变量的取值范围是

则的分布列：
（3）不正确； 举例：，排名前的成绩均为分，方差为，排名后的成绩均为分，
方差为，显然，所以，，故同时大于和.
随堂练习：答案：（1） ；（2）详见解析；（3）2200
解:（1）在随机抽取的100名顾客中，年龄在[30,50)且未使用自由购的共有3+14=17人，
所以，随机抽取1名顾客，估计该顾客年龄在[30,50)且未使用自由购的概率为．
（2）所有的可能取值为1,2,3，
, , .
所以的分布列为
所以的数学期望为.
（3）在随机抽取的100名顾客中， 使用自由购的共有人，
所以该超市当天至少应准备环保购物袋的个数估计为.
典例6、答案： （1） （2）分布列答案见解析，数学期望：1 （3）
解：（1）设选取的乘客在积水潭站上车､在牛街站下车为事件，
由已知，在积水潭站上车的乘客有人，其中在牛街站下车的乘客有人，
所以.
（2）由题意可知，
； ；
； .
随机变量的分布列为
所以随机变量的数学期望为：. .
（两点分布：）
随堂练习：答案：（1）0.9 （2）分布列见详解，
（3）当该纪念品的销售价格定为110元时， 达到最大值．
解：（1）时，消费者购买该纪念品的概率
由题意，，，
，同理，，，，
的分布列为：
.
（2）由（2）知时，（时等号成立），
时，（时等号成立），
时，（时等号成立），
，因此最大，此时．
所以当该纪念品的销售价格定为110元时，Y的数学期望达到最大值．
收看
没收看
男生
60
20
女生
20
20
0.10
0.05
0.025
0.01
0.005
2.706
3.841
5.024
6.635
7.879
学业优秀
学业不优秀
总计
体育成绩不优秀
100
200
300
体育成绩优秀
50
50
100
总计
150
250
400
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.01
0.005
0.001
0.46
0.71
1.32
2.07
2.71
3.84
5.024
6.635
7.879
10.828
愿意接种
不愿意接种
合计
男
女
合计
0.050
0.010
0.005
3.841
6.635
7.879
球队胜
球队负
总计
甲参加
甲未参加
总计
参加社团
未参加社团
合计
男生
女生
合计
0.1
0.05
0.01
2.706
3.841
6.635
年龄