






初中数学人教版(2024)八年级上册第十五章 分式15.1 分式15.1.1 从分数到分式教课内容ppt课件
展开复习回顾问题1请同学们回顾教材103页的例7和例8.思考:我们学过的整式的除法有什么类型?除法的结果有什么特点? 通过以下两道例题,回顾整式的除法运算.
例8计算:(1)28x⁴y²÷7x³y;(2)-5a⁵b³c÷15a⁴b;(3)(12a³-6a²+3a)÷3a.
例7计算:(1)x⁸÷x²(2)(ab)⁵÷(ab)²
例8:解:(1)28x⁴y²÷7x³y=(28÷7)·x⁴-3·y²-1=4xy(2)-5a⁵b³c÷15a⁴b=[(-5)÷15]a⁵-4b³-1c(3)(12a³-6a²+3a)÷3a=12a³÷3a-6a²÷3a+3a÷3a=4a²-2a+1
结果仍然是一个整式.例7:解(1)x⁸÷x²=x⁸-²=x⁶ ;(2)(ab)⁵÷(ab)²=(ab)⁵-2 =(ab)³=a³b³
除法分为单项式除单项式;多项式除单项式的形式,整式除法的计算
概念引出问题2整式除以整式,结果一定是整式吗?请大家举出几个整式除以整式, 结果不是整式的例子.
追问1:你觉得写出的这些例子是不是都符合问题的要求?哪几个不符合,为什么?追问2:a÷(m+n) 的结果你用 的形式表示,你是怎么想到用这种形式表示的呢?
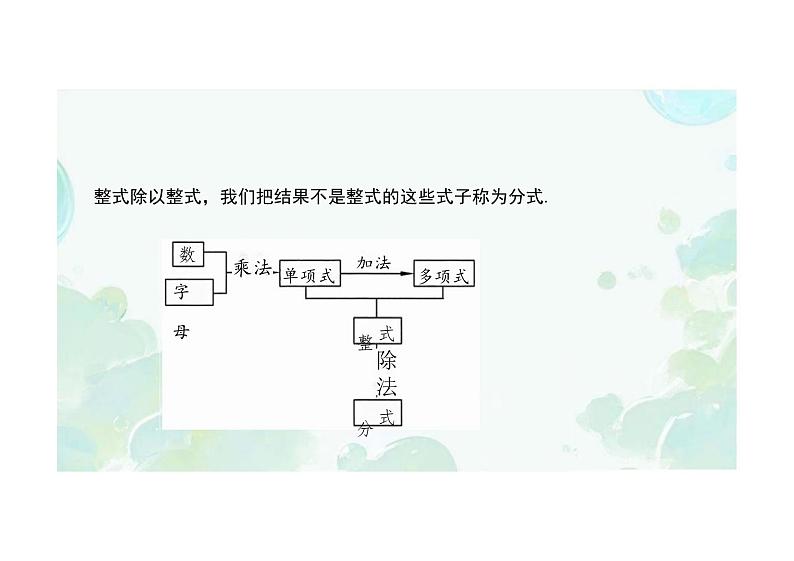
整式除以整式,我们把结果不是整式的这些式子称为分式.
式 除 法 式 整 分
问题3根据前面的分析,分式具有什么样的特征呢?观察式子的结构特征, 并将其与分数的结构特征进行比较,能够类比分数给分式下定义吗?
追问:你可以给分式下定义吗?分式的定义:形如 ,A,B 是整式,且B中含有字母的式子叫做分式
分析:判断一个式子是否为 分式,要抓住分式的定义的几个关键词: 的形式,A,B表示两个整式,B中含字母. 这样我们就可以判断一个代 数式是否为分式了.
理解概念判断下列各式是不是分式?为什么?
注意:由于π是个特殊的字母,它表示圆周率这一特定的数,因而是整式,而不是分式;虽然 但是等号左右两侧的代数式中字母x的取值范围不同,也就是说两个式子的含义不相同,所以判断一个式子是 否为分式,不可约分.提升:判断分式一定要注意定义的关键词.另外,分式是形式定义,不要看化简结果.
在表格中填入计算结果:
问题4 分式何时有意义?归纳:分式有意义的条件是分母不等于零.即分式 有意义的条件是B≠0.
典例分析例1(1)当x是什么数时,分式 的值是零?( 2 ) 当x是什么数时,分式 的值是零?分析:对于分式 手 分式值为零的条件是:分子的值为零,且分母的值不为零.即
解:(1)由分子x+2=0, 得x=-2.而此时2x-5=-9≠0, 当x=-2时 ,分式 的值是零.( 2 ) 分 式 的值为零的条件是 即 由 |x|=3 可得x=3 或x=-3, 显然x=-3舍去,∴当x=3时,分 的值是零.提升:当求使分式值为零的字母的取值时,我们可以先求满足分子的值为零 时字母的值,再代入分母,检验是否为零,舍掉使分母为零的值;也可以直 接利用分子的值为零、分母的值不为零这两个条件共同确定字母的取值.
例2(1)若分式 的值为1,求x 的值.(2)若分式 的值为正数,求x 的取值范围解(1)由题意得x+1=3x-2得 ,又∵3x-2=≠0,得 所求.(2)由题意得: 解不等式组①,得 解不等式组②,得x<-1,所以,当 或x<-1时,分式 的值为正数.
提升:(1)求得满足条件的结果时一定要检验分母不为0,即分式有意义;(2)分式值为正:分子分母同号;(3)分式值为负:分子分母异号.
练习巩固课堂练习:1.下列各式中,哪些是整式?哪些是分式?思考1:分式概念中的关键词是什么?
思考2:分式有意义、无意义的条件是什么?
2.当x取何值时,下列分式有意义?
3.当x取何值时,下列分式的值为零?
思考3:分式的值为0的条件是什么?
变式1. (1)分式 的值为1,求x 的值.(2)分式 的值为-1,求x 的取值变式2.当x为何值时,下列分式的值为正数?
思考4:若把题目要求改为:当x为何值时,分式的值为负数,结果会怎样?
2.使分式 有意义的x的取值范围是( )A.x=2B.x≠2C.x=-2D.x≠-2
达标检测1.在式子 1,2,
中,是分式的有 .
3.对单项式“5x”, 我们可以这样解释:香蕉每千克5元,某人买了xkg,共付款5x元.请你对分式 给出一个实际生活方面的合理解释.4.从3,x,2x-1 中任意选取两个不同的整式相除,组成的分式有 .
达标检测 B级1.下列分式中,一定有意义的是( )Ax-5B C. D.2.当x取何值时,下列式子的值为零?(1)当x=______时, 的值为0.(2)当x=_____时 , 的值为0
3.当x取何值时,分式 的值为-1.4.若一个分式含有字母m, 且 当m=5 时,它的值为12.则这个分式可以是 . (写出一个即可,答案不唯一)5.已知分式 ,当x=-4时,该分式没有意义;当x=-5 时,该分式的值为0. 求(m+n)²016 的值.6.若分式 有意义,则x,y 要满足什么条件?
达标检测 C级1.求下列分式有意义时字母满足的条件.(1) ;(2) 重2.求当x取何值时,下列式子的值为零?(1) ;(2)
3.求当x取何值时,分式 的值:(1)为正数;(2)为负数4.当x为何值时,分式 的值是非负数?
人教版八年级上册15.1.1 从分数到分式教学课件ppt: 这是一份人教版八年级上册15.1.1 从分数到分式教学课件ppt,共33页。PPT课件主要包含了学习目标,新课导入,复习引入,整式包括什么,包括单项式和多项式,①⑤⑦,②④⑧,①②④⑤⑦⑧,练一练,新知探究等内容,欢迎下载使用。
初中数学人教版八年级上册15.1.1 从分数到分式示范课ppt课件: 这是一份初中数学人教版八年级上册15.1.1 从分数到分式示范课ppt课件,共12页。PPT课件主要包含了①③⑤,x≠-3等内容,欢迎下载使用。
数学人教版15.1.1 从分数到分式教学ppt课件: 这是一份数学人教版15.1.1 从分数到分式教学ppt课件,共20页。PPT课件主要包含了课堂讲解,课时流程,逐点导讲练,课堂小结,作业提升,知识点,分式的定义,都具有分数的形式,相同点,不同点等内容,欢迎下载使用。













