数学八年级上册15.1.1 从分数到分式优质教学作业课件ppt

这是一份数学八年级上册15.1.1 从分数到分式优质教学作业课件ppt，文件包含1511从分数到分式pptx、1511从分数到分式同步练习解析版docx、1511从分数到分式教学设计docx、1511从分数到分式同步练习原卷版docx、1511从分数到分式导学案docx等5份课件配套教学资源，其中PPT共25页， 欢迎下载使用。

15.1.1 从分数到分式
人教版数学八年级上册
1.了解分式的概念.2.理解分式有意义的条件及分式值为零、为正、为负的条件．（重点）3.能熟练地求出分式有意义的条件及分式值为零、为正、为负的条件．(难点)
1.下列两个整数相除如何表示成分数的形式： 3÷4= 10÷3= 12÷11= -7÷2=2.在代数式中，整式的除法是否也能类似地表示？试用类似分数的形式表示下列整式的除法：(1) 90÷x 可以用式子( )来表示；60÷(x-6)可以用式子( )来表示.(2) n 公顷麦田共收小麦 m 吨，平均每公顷产量可以用式子( )吨来表示.
 
 
 
 
章前引言 一艘轮船在静水中的最大航速为30km/h，它以最大船速沿江顺流航行90km所用时间，与以最大航速逆流航行60km所用的时间相等，江水的流速是多少？
如果设江水的流速为vkm/h，则轮船顺流航行90km所用时间为_________h，逆流航行60km所用时间为_________h，由方程_________________可以解出 v 的值.
填空： (1)长方形的面积为10cm2，长为7cm，则宽为____cm；长方形的面积为S，长为a，宽应为______.(2)把体积为200cm3的水倒入底面积为33cm2的圆柱形容器中，则水面高度为______cm；把体积为V的水倒入底面积为S的圆柱形容器中，则水面高度为_____.
式子 ， ， ， ， ， ， ，有什么共同点？它们与分数有什么相同点和不同点？
可以发现，这些式子与分数一样都是 (即A÷B)的形式. 分数的分子A与分母B都是整数，而这些式子中的A，B都是整式，并且B中都含有字母.
一般地，如果A、B都表示两个整式，并且B中含有字母，那么式子 叫做分式.其中A叫做分式的分子，B为分式的分母.
 
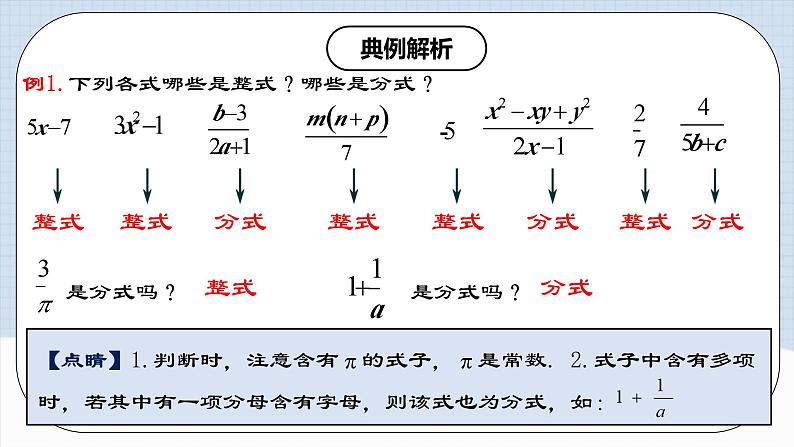
例1.下列各式哪些是整式？哪些是分式？
整式
整式
分式
整式
分式
整式
分式
整式
整式
分式
我们知道，要使分数有意义，分数中的分母不能为0.要使分式有意义，分式中的分母应满足什么条件？
例2.下列分式中的字母满足什么条件时分式有意义？
解：(1)要使分式 有意义，则分母3x≠0，即x≠0； (2)要使分式 有意义，则分母x-1≠0，即x≠1； (3)要使分式 有意义，则分母5-3b≠0，即b≠ ； (4)要使分式 有意义，则分母x-y≠0，即x≠y.
例3.已知分式 有意义，则x应满足的条件是 (　　) A.x≠1 B．x≠2 C.x≠1且x≠2 D.以上结果都不对
C
【点睛】分式有意义的条件是分母不为零.如果分母是几个因式乘积的形式，则每个因式都不为零.
下列分式中的字母满足什么条件时分式有意义？
 
分式 的值为零应满足什么条件？分式 的值为正(负)应满足什么条件？
根据除法的意义及法则很容易得到：
解：当分子等于零而分母不等于零时,分式的值为零.则x2-1=0，∴x=±1，而x+1≠0，∴x≠-1.∴当x=1时分式 的值为零.
例4.当x为何值时，分式 的值为零?
1.当 时，分式 的值为零.
x=2
2.若 的值为零，则x＝ ．
－3
 
 
D
 
C
B
 
C
B
D
 
C
B
-2
-4
 
 
2或3或5
 
 
 
解：由题意得，x-1≠0，x+2≠0，解得x≠1且x≠-2．
 
 
 
 
 
 
 
一般地，如果A、B都表示两个整式，并且B中含有字母，那么式子 叫做分式.其中A叫做分式的分子，B为分式的分母.