人教版（2024）八年级上册12.1 全等三角形教案配套ppt课件

这是一份人教版（2024）八年级上册12.1 全等三角形教案配套ppt课件，共60页。
一、选择题(每小题3分,共30分)
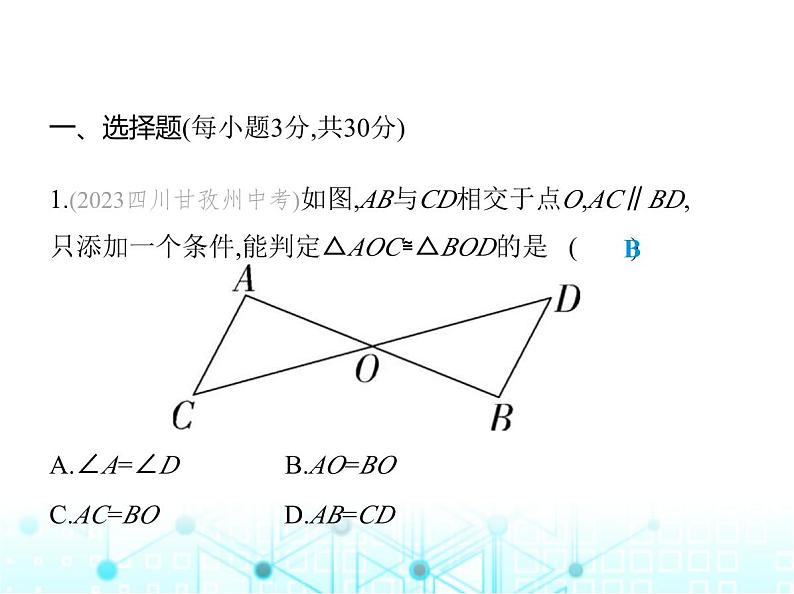
1.(2023四川甘孜州中考)如图,AB与CD相交于点O,AC∥BD, 只添加一个条件,能判定△AOC≌△BOD的是 (　    ) A.∠A=∠D　　　    B.AO=BOC.AC=BO　　　     D.AB=CD
解析　由AC∥BD可得∠A=∠B,∠C=∠D,当AO=BO时,可利 用AAS判定△AOC≌△BOD,故选B.
2.(情境题·中华优秀传统文化)(2022江苏扬州中考)如图,小明 家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块. 小明通过电话给玻璃店老板提供相关数据,为了方便表述,将 该三角形记为△ABC,提供下列各组元素的数据,配出来的玻 璃不一定符合要求的是 (　    ) 
A.AB,BC,CA　　　     B.AB,BC,∠BC.AB,AC,∠B　　　    D.∠A,∠B,BC
解析    选项A,利用三边分别相等的两个三角形全等可确定 三角形形状,故此选项不合题意;选项B,利用两边和它们的夹 角分别相等的两个三角形全等可确定三角形形状,故此选项 不合题意;选项C,由AB,AC,∠B无法确定三角形的形状,故此 选项符合题意;选项D,根据两角分别相等且其中一组等角的 对边相等的两个三角形全等可确定三角形形状,故此选项不 合题意.
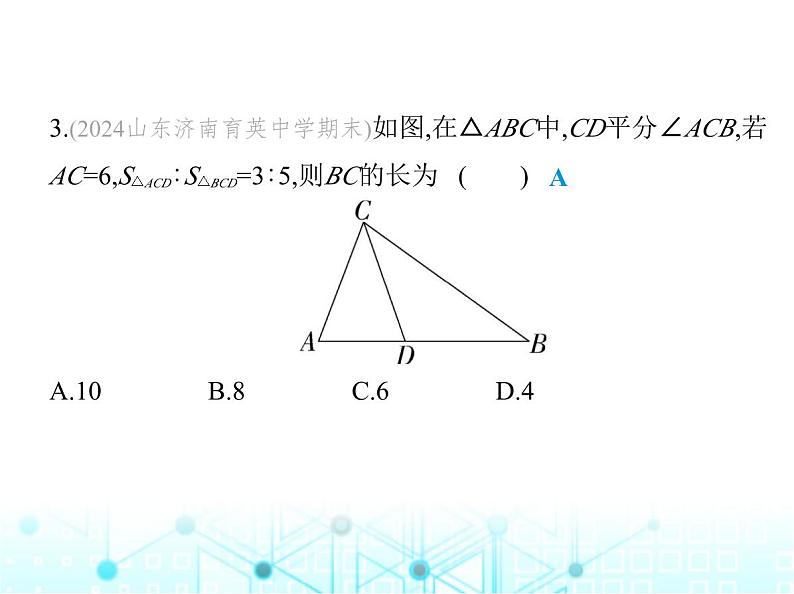
3.(2024山东济南育英中学期末)如图,在△ABC中,CD平分∠ACB,若AC=6,S△ACD∶S△BCD=3∶5,则BC的长为 (　    ) A.10　　　    B.8　　　    C.6　　　    D.4
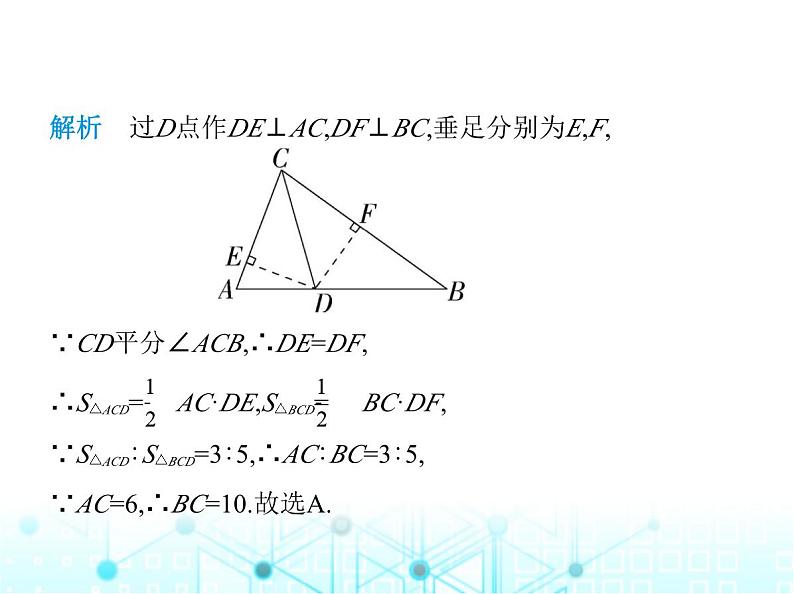
解析　过D点作DE⊥AC,DF⊥BC,垂足分别为E,F, ∵CD平分∠ACB,∴DE=DF,∴S△ACD= AC·DE,S△BCD= BC·DF,∵S△ACD∶S△BCD=3∶5,∴AC∶BC=3∶5,∵AC=6,∴BC=10.故选A.
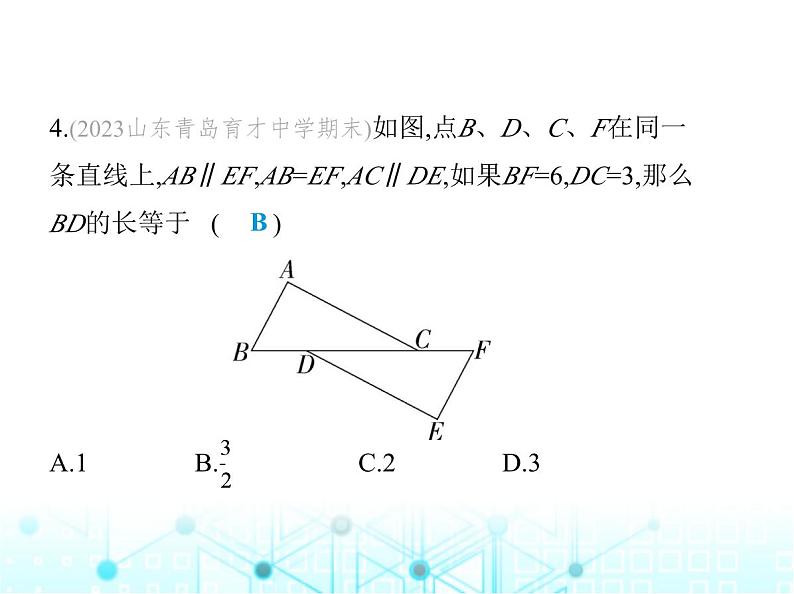
4.(2023山东青岛育才中学期末)如图,点B、D、C、F在同一 条直线上,AB∥EF,AB=EF,AC∥DE,如果BF=6,DC=3,那么 BD的长等于 (　    ) A.1　　　    B. 　　　    C.2　　　    D.3
解析　∵AB∥EF,∴∠B=∠F,∵AC∥DE,∴∠ACB=∠EDF,在△ABC和△EFD中, ∴△ABC≌△EFD(AAS),∴BC=FD,∴BC-DC=FD-DC,∴BD=FC,∴BD= (BF-DC)= ×(6-3)= .故选B.
5.如图,在△ABC中,AB=AC,BC≠AB,BD,CE为中线且交于点 F,连接AF,则图中的全等三角形共有 (　    ) A.3对　　　    B.4对　　　    C.5对　　　    D.6对
解析　∵AB=AC,BD、CE为中线,∴AD=DE=BE=CD,∵∠BAD=∠CAE,∴△ABD≌△ACE,∴BD=CE,∠ABD=∠ACE,∠ADB=∠AEC,∴∠BEC=∠CDB,∵BE=CD,∴△BEC≌△CDB,∵∠EFB=∠DFC,∠BEF=∠CDF,BE=CD,∴△BEF≌△CDF,∴EF=DF,BF=CF,∵AE=AD,∠AEF=∠ADF,∴△AEF≌△ADF,∵BF=CF,∠ABF=∠ACF,AB=AC,∴△ABF≌△ACF,∴共有5对全等三角形.故选C.
6.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半 径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于  MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是(　    ) A.15　　　    B.30C.45　　　    D.60
解析　过点D作DE⊥AB于E,如图, 由题意得AP是∠BAC的平分线,∠C=90°,∴DE=CD=4, ∴△ABD的面积= AB·DE= ×15×4=30.故选B.
7.如图,点B,C,E在同一条直线上,且AC=CE,∠B=∠D=90°,AC ⊥CD,下列结论不一定成立的是 (　    ) A.∠A=∠2　　　    B.∠A+∠E=90°C.BC=DE　　　     D.∠BCD=∠ACE
解析　∵AC⊥CD,∴∠ACD=90°,∴∠1+∠2=90°,∵∠B=90°,∴∠1+∠A=90°,∴∠2=∠A,在△ABC和△CDE中, ∴△ABC≌△CDE(AAS),∴BC=DE,∠1=∠E,∴∠A+∠E=90°,∵∠1不一定等于∠2,∴∠BCD不一定等于∠ACE.故选D.
8.如图,在四边形ABCD中,AB∥DC,E为BC的中点,连接DE、 AE,AE⊥DE,延长DE交AB的延长线于点F.若AB=5,CD=3,则 AD的长为 (　    ) A.2　　　    B.5　　　    C.8　　　    D.11
解析　∵E为BC的中点,∴BE=EC,∵AB∥CD,∴∠F=∠CDE,在△BEF与△CED中, ∴△BEF≌△CED(AAS),∴EF=DE,BF=CD=3,∴AF=AB+BF=8,在△AEF与△AED中, 
∴△AEF≌△AED(SAS),∴AD=AF=8,故选C.
9.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E, 有下列结论:①CD=ED;②AC+BE=AB;③DA平分∠CDE;④∠BDE=∠BAC;⑤S△ABD∶S△ACD=AB∶AC.其中正确的个数为(        ) A.5　　　    B.4　　　    C.3　　　    D.2
解析　∵在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,∴CD=ED,故①正确;在Rt△ADE和Rt△ADC中, ∴Rt△ADE≌Rt△ADC(HL),∴∠ADE=∠ADC,AE=AC,∴DA平分∠CDE,故③正确;∵AE=AC,∴AB=AE+BE=AC+BE,故②正确;∵∠BDE+∠B=90°,∠B+∠BAC=90°,∴∠BDE=∠BAC,故④正确;
∵S△ABD= AB·DE,S△ACD= AC·CD,且CD=ED,∴S△ABD∶S△ACD=AB∶AC,故⑤正确.故正确结论的个数为5,故选A.
10.(2024山东日照期末)如图,在△ABD和△ACE中,AB=AD, AC=AE,AB>AC,∠DAB=∠CAE=50°,连接BE,CD交于点F,连 接AF.下列结论:①BE=CD;②∠EFC=50°;③AF平分∠DAE; ④FA平分∠DFE.其中正确的个数为 (　    )A.1　　　    B.2　　　    C.3　　　    D.4
解析　∵∠DAB=∠CAE=50°,∴∠BAE=∠DAC=50°+∠BAC,在△BAE和△DAC中, ∴△BAE≌△DAC(SAS),∴BE=CD,∠AEB=∠ACD,故①正确;如图,设BE交AC于点G,∴∠EFC=∠CGE-∠ACD=∠CGE-∠AEB=∠CAE=50°,故②正确;
 过A作AI⊥BE于点I,AJ⊥CD于点J,∵S△BAE=S△DAC,∴ AI·BE= AJ·CD,∵BE=CD,∴AI=AJ,∴点A在∠DFE的平分线上,∴FA平分∠DFE,故④正确;
假设∠DAF=∠EAF,则∠DAF-∠DAB=∠EAF-∠CAE,∴∠BAF=∠CAF,∵∠AFD=∠AFE,∠BFD=∠CFE,∴∠AFD+∠BFD=∠AFE+∠CFE,∴∠AFB=∠AFC,在△AFB和△AFC中, ∴△AFB≌△AFC(ASA),∴AB=AC,
与已知条件矛盾,∴∠DAF≠∠EAF,故③错误,∴正确结论的个数为3,故选C.
二、填空题(每小题3分,共24分)
11.已知△ABC的三边长分别为3,5,7,△DEF的三边长分别为 3,7,2x-1,若这两个三角形全等,则x的值是　　　　    .
解析　∵△ABC与△DEF全等,∴2x-1=5,∴x=3.
12.如图,在6×6的正方形网格中,正方形ABCD的顶点均在格 点上,格点E,F分别在AB,BC上,连接AF,DE交于点O,连接DF, 则∠AFD+∠EDF=　　　　    . 
解析　由题意知DA=AB,AE=BF,∠DAE=∠ABF=90°,∴△DAE≌△ABF(SAS),∴∠ADE=∠BAF, ∵∠BAF+∠DAF=90°,∴∠ADE+∠DAF=90°,∴∠DOF=∠AOD=90°,∴∠AFD+∠EDF=90°.
13.(2023江苏扬州期末改编)如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,△ABC的面积是30 cm2,AB=13 cm,AC=7 cm,则DE的长为　　　　    . 
解析　∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,∵S△ABC= AB·DE+ AC·DF,∴ ×13DE+ ×7DF=30,∴DE=3 cm.
14.(一题多解)(2022湖南株洲中考)如图所示,点O在一块直角 三角板ABC上(其中∠ABC=30°),OM⊥AB于点M,ON⊥BC于 点N,若OM=ON,则∠ABO=　　　　    度. 
解析　解法一:∵OM⊥AB,ON⊥BC,∴∠OMB=∠ONB=90°,在Rt△OMB和Rt△ONB中, ∴Rt△OMB≌Rt△ONB(HL),∴∠OBM=∠OBN,∵∠ABC=30°,∴∠ABO=15°.解法二:∵OM⊥AB,ON⊥BC,OM=ON,∴BO平分∠ABC,∴∠OBM=∠OBN,∵∠ABC=30°,∴∠ABO=15°.
15.如图,五边形ABCDE中,AB=DE,BC=AE,连接AC,AD,AC= AD,∠ACD=∠ADC=70°,若∠E=95°,则∠BAE的度数为　    　　    . 
解析　在△ABC与△DEA中, ∴△ABC≌△DEA(SSS),∴∠B=∠E=95°,∠ACB=∠DAE,∴∠BAC+∠ACB=∠BAC+∠DAE=180°-95°=85°,∵∠ACD=∠ADC=70°,∴∠CAD=180°-2×70°=40°,∴∠BAE=∠BAC+∠DAE+∠CAD=85°+40°=125°.
16.(2022广东广州六中月考)如图,小张同学拿着老师的等腰 直角三角尺,摆放在两摞长方体教具之间,∠ACB=90°,AC= BC,若每个长方体教具的高度均为6 cm,则两摞长方体教具 之间的距离DE为　　　　    cm. 
解析　由题意得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,∠ACD+∠BCE=90°,∴∠ACD+∠DAC=90°,∴∠BCE=∠DAC,在△ADC和△CEB中, ∴△ADC≌△CEB(AAS),∴CD=BE,AD=CE,
∵DE=CD+CE,∴DE=BE+AD,∵一个长方体教具的高度为6 cm,∴AD=24 cm,BE=18 cm,∴两摞长方体教具之间的距离DE为 24+18=42(cm).
17.(构造法)如图,将一块等腰直角三角板ABC(AC=BC)的直 角顶点C按如图所示的方式放在平面直角坐标系的y轴上,点 A在x轴上,已知AO=3,OC=1,则点B的坐标为　　　　    . 
解析　如图,过B作BD⊥y轴于D, 则∠DCB+∠DBC=90°,∵∠ACB=90°,∴∠DCB+∠ACO=90°,∴∠DBC=∠ACO,
在△CBD和△ACO中, ∴△CBD≌△ACO(AAS),∴BD=OC=1,CD=OA=3,∴OD=OC+CD=4,∴点B的坐标为(1,4).
18.(2024湖南长沙长郡中学期末)如图,AD是△ABC的角平分 线,DF⊥AB于点F,点E,G分别是边AB,AC上的点,且DE=DG, 则∠AED+∠AGD=　　　　    度. 
解析　如图,过点D作DH⊥AC于点H, ∵DF⊥AB,AD是△ABC的角平分线,∴DF=DH,∵DE=DG,∴△DEF≌△DGH(HL),∴∠AGD=∠DEF,∴∠AED+∠AGD=∠AED+∠DEF=180°.
三、解答题(共46分)
19.(2022江苏淮安中考)(6分)如图,点A、D、C、F在同一条 直线上,且AD=CF,AB=DE,∠BAC=∠EDF.求证:∠B=∠E. 
证明　∵AD=CF,∴AD+CD=CF+CD,∴AC=DF.在△ABC和△DEF中, ∴△ABC≌△DEF(SAS),∴∠B=∠E.
20.(2023陕西中考A卷)(6分)如图,在△ABC中,∠B=50°,∠C= 20°,过点A作AE⊥BC,垂足为E,延长EA至点D,使AD=AC,在边 AC上截取AF=AB,连接DF.求证:DF=CB. 
证明　在△ABC 中,∠B=50°,∠C=20°,∴∠CAB=180°-∠B-∠C=110°.∵AE⊥BC,∴∠AEC=90°.∴∠DAF=∠AEC+∠C=110°,∴∠DAF=∠CAB.在△DAF和△CAB中, ∴△DAF≌△CAB(SAS),∴DF=CB.
21.(6分)如图,在△ABC中,D为AB上一点,E为AC的中点,连接 DE并延长至点F,使得EF=ED,连接CF.(1)求证:CF∥AB.(2)若∠ABC=50°,连接BE,BE平分∠ABC,CA平分∠BCF,求∠A的度数. 
解析    (1)证明:在△AED和△CEF中, ∴△AED≌△CEF(SAS),∴∠A=∠ACF,∴CF∥AB.(2)∵CA平分∠BCF,∴∠ACB=∠ACF,∵∠A=∠ACF,∴∠A=∠ACB,∵∠A+∠ABC+∠ACB=180°,∠ABC=50°,∴2∠A=130°,∴∠A=65°.
22.(2023北京西城期中)(8分)如图,点B,C,E在同一条直线上, CD平分∠ACE,∠DBM=∠DAN,DM⊥BE于M,DN⊥AC于N.(1)求证:△BDM≌△ADN.(2)若AC=7,BC=3,求CM的长. 
解析    (1)证明:∵CD平分∠ACE,DM⊥BE,DN⊥AC,∴DM=DN,∠DMB=∠DNA=90°,在△BDM和△ADN中, ∴△BDM≌△ADN(AAS).(2)由(1)知DM=DN,在Rt△DCN和Rt△DCM中, ∴Rt△DCN≌Rt△DCM(HL),∴CN=CM,
由(1)知△BDM≌△ADN,∴BM=AN,∴AC=AN+CN=BM+CM=BC+CM+CM=7,∴3+2CM=7,∴CM=2.
23.(2024河南郑州枫杨外国语学校期中)(10分)如图,在△ABC中,AP平分∠BAC,CP平分∠ACB,作PD⊥AB于点D,连接BP.(1)求证:BP平分∠ABC.(2)已知△ABC的面积为15,AB=4,AC=4,BC=2,求PD的长.(3)当AB=7,BC=5,AC=8时,求BD的长.
解析    (1)证明:如图,过P作PE⊥BC,PF⊥AC,垂足分别为E,F,∵AP平分∠BAC,CP平分∠ACB,PD⊥AB,∴PD=PF,PE=PF,∴PD=PE,∴BP平分∠ABC.(2)由(1)可得PD=PE=PF,∴S△ABC=S△PAB+S△PBC+S△PAC= AB·PD+ BC·PE+ AC·PF= ×4×
PD+ ×2×PD+ ×4×PD= PD×(4+2+4)=5PD=15,∴PD=3.(3)由(1)知BP平分∠ABC,∴∠PBC=∠PBA,在△PBE和△PBD中, ∴△PBE≌△PBD(AAS),∴BE=BD,同理可得CE=CF,AD=AF,设BD=BE=x,则AD=AF=AB-BD=7 -x,CE=CF=BC-BE=5-x,∴AC=CF+AF=5-x+7-x=8,解得x=2,即 BD=2.
24.(2022山东日照模拟)(10分)在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且 ∠EAF=60°,试探究图1中线段BE、EF、FD之间的数量关系.(1)小亮同学认为:延长FD到点G,使DG=BE,连接AG,先证明 △ABE≌△ADG,再证明△AEF≌△AGF,则可得到BE、 EF、FD之间的数量关系:　　　　    .(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分 别是BC、CD上的点,∠EAF= ∠BAD,上述结论是否仍然成
解析    (1)EF=BE+DF.详解:在△ABE和△ADG中, ∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,∵∠BAD=120°,∠EAF=60°,∴∠EAF= ∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF= 60°=∠EAF,
在△AEF和△AGF中, ∴△AEF≌△AGF(SAS),∴EF=FG,∵FG=DG+DF=BE+DF,∴EF=BE+DF.(2)结论EF=BE+DF仍然成立.理由:如图,延长FD到点G,使DG=BE,连接AG,
 ∵∠B+∠ADF=180°,∠ADF+∠ADG=180°,∴∠B=∠ADG,在△ABE和△ADG中, ∴△ABE≌△ADG(SAS),