

还剩31页未读,
继续阅读
成套系列资料,整套一键下载
人教A版(2019)必修第二册第8章立体几何初步重难点归纳总结(原卷版+解析)
展开
这是一份人教A版(2019)必修第二册第8章立体几何初步重难点归纳总结(原卷版+解析),共34页。
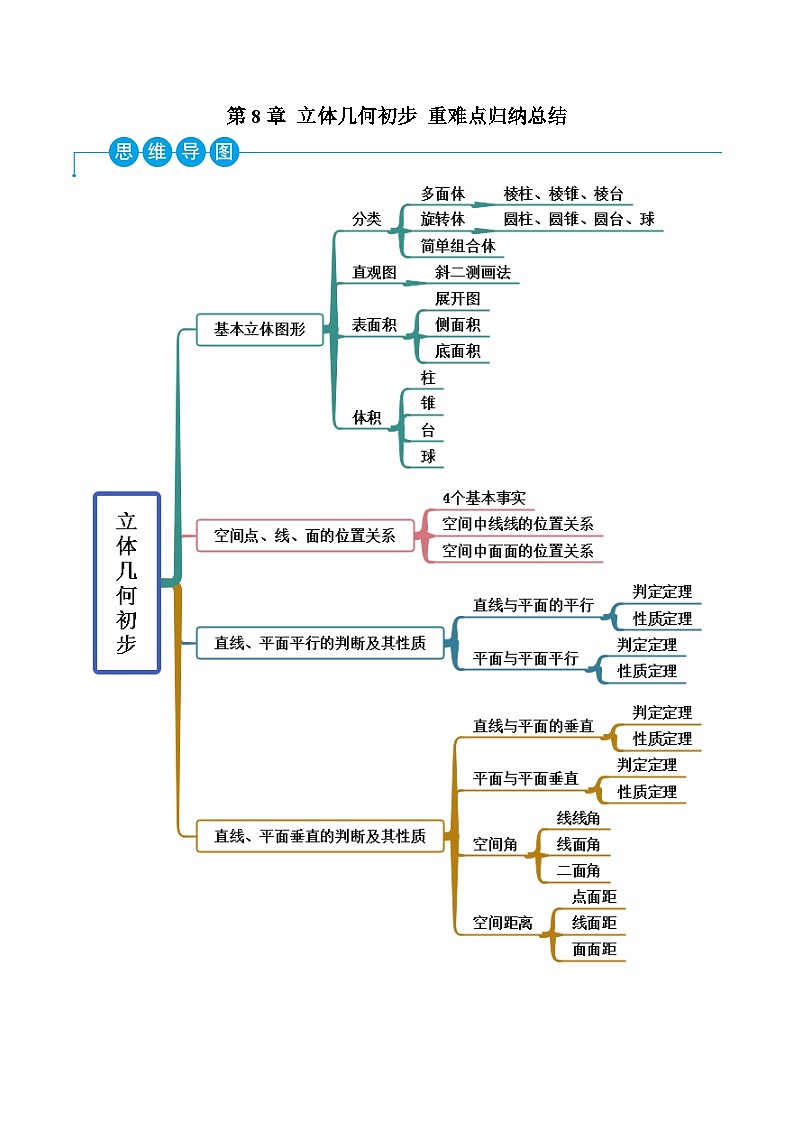
第8章 立体几何初步 重难点归纳总结考点一 体积【例1】(2023浙江丽水)已知一个圆锥的底面半径为1,其侧面积是底面积2倍,则圆锥的体积为( )A. B. C. D.【一隅三反】1.(2023·江西)陀螺是中国民间最早的娱乐工具之一,也称陀罗.图1是一种木陀螺,可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图2所示,其中分别是上、下底面圆的圆心,且,底面圆的半径为2,则该陀螺的体积是( )A. B. C. D.2.(2022秋·吉林)如图是一个棱长为2的正方体被过棱、的中点、,顶点和过点顶点、的两个截面截去两个角后所得的几何体,则该几何体的体积为( )A.5 B.6 C.7 D.83.(2023·河南信阳)已知圆台上下底面半径之比为1:2,母线与底面所成的角为60°,其侧面面积为,则该圆台的体积为( )A. B. C. D.4.(2023·浙江)(多选)圆柱的侧面展开图是长4cm,宽2cm的矩形,则这个圆柱的体积可能是( )A. B.C. D.考点二 表面积【例2】(2023辽宁)已知四棱台的上、下底面分别是边长为和的正方形,侧面均为腰长为的等腰梯形,则该四棱台的表面积为( )A. B.C. D.【一隅三反】1.(2023江苏无锡)为了给热爱朗读的师生提供一个安静独立的环境,某学校修建了若干“朗读亭”.如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,正六棱柱两条相对侧棱所在的轴截面为正方形,若正六棱锥与六棱柱的高的比值为1∶3,则正六棱锥与正六棱柱的侧面积之比为( )A. B. C. D.2(2022上海徐汇)若圆台的高是4,母线长为5,侧面积是,则圆台的上、下底面的面积之和是______.考点三 直线、平面平行【例3】(2022山东聊城)由四棱柱截去三棱锥后得到的几何体如图所示,四边形为平行四边形,O为与的交点.(1)求证:∥平面;(2)求证:平面∥平面;(3)设平面与底面的交线为l,求证:.【一隅三反】1.(2022青海海南)如图,四边形是矩形,平面,平面.(1)证明:平面平面.(2)若平面与平面的交线为,求证:2.(2022秋·贵州)正的边长为2,是边上的高,E,F分别是和的中点(如图甲).现将沿翻成直二面角(如图乙).在图乙中:(1)求证:平面;(2)求点到平面的距离.3.(2022秋·上海)(1)叙述两个平面平行的判定定理,并证明;(2)如图,正方体中,分别为的中点,求证:平面平面.考点四 直线、平面垂直【例4】(2023浙江丽水)(多选)已知正方体是中点,则( )A.面 B.C. D.平面【一隅三反】1.(2023·海南)(多选)在长方体中,,,则下列线段与垂直的有( )A. B. C. D.2.(2022秋·河北唐山)(多选)如图,在长方体中,M,N分别为棱,的中点,则下列判断正确的是( ).A.直线与是异面直线 B.平面C.平面 D.3.(2022秋·青海海东)如图,已知四棱锥的底面ABCD是菱形,,点E为PC的中点.(1)求证:平面BDE;(2)求证:平面平面PAC.考点五 空间角【例5】(2022·浙江)(多选)《九章算术·商功》:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳌臑.”其中,阳马是底面为矩形,且有一条侧棱与底面垂直的四棱锥.如图,在阳马中底面是边长为1的正方形,,侧棱垂直于底面,则( )A.直线与所成的角为60°B.直线与所成的角为60°C.直线与平面所成的角为30°D.直线与平面所成的角为30°【一隅三反】1.(2022春·广西桂林·高二校考期中)如图,在四棱锥中,PD⊥底面ABCD,四边形ABCD为正方形,且,G为△ABC的重心,则PG与底面ABCD所成的角的正弦值等于( )A. B. C. D.2.(2022上海黄浦)过正方形ABCD之顶点A作平面,若,则平面与平面所成的锐二面角的度数为________.3.(2022秋·四川达州)如图,在四棱锥中,面,,,点分别为的中点,,.(1)证明:直线平面;(2)求二面角的余弦值.考点六 空间距离【例6-1】(2022秋·重庆南岸·高二重庆市第十一中学校校考期末)如图,在直三棱柱中,是等边三角形,,是棱的中点.求点到平面的距离等于_______【一隅三反】1.(2022秋·上海黄浦)的三边长分别为3、4、5,为平面外一点,它到三边的距离都等于2,则到平面的距离是________.2.(2022秋·上海黄浦)若正四棱柱的底面边长为,与底面成角,则到底面的距离为__________.3.(2023重庆巫山)如图,在四棱锥中,底面是菱形,,平面平面,,,PD的中点为F.(1)求证:平面;(2)求直线到面的距离.4.(2023浙江)已知正方体的棱长均为1.(1)求到平面的距离;(2)求平面与平面之间的距离. 第8章 立体几何初步 重难点归纳总结考点一 体积【例1】(2023浙江丽水)已知一个圆锥的底面半径为1,其侧面积是底面积2倍,则圆锥的体积为( )A. B. C. D.【答案】B【解析】设圆锥的母线为l,由题意得,解得,所以圆锥的高为,所以圆锥的体积为,故选:B【一隅三反】1.(2023·江西)陀螺是中国民间最早的娱乐工具之一,也称陀罗.图1是一种木陀螺,可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图2所示,其中分别是上、下底面圆的圆心,且,底面圆的半径为2,则该陀螺的体积是( )A. B. C. D.【答案】D【解析】已知底面圆的半径,由,则,故该陀螺的体积.故选:D.2.(2022秋·吉林)如图是一个棱长为2的正方体被过棱、的中点、,顶点和过点顶点、的两个截面截去两个角后所得的几何体,则该几何体的体积为( )A.5 B.6 C.7 D.8【答案】C【解析】如图将正方体还原可得如下图形:则,,,所以该几何体的体积.故选:C3.(2023·河南信阳)已知圆台上下底面半径之比为1:2,母线与底面所成的角为60°,其侧面面积为,则该圆台的体积为( )A. B. C. D.【答案】D【解析】圆台轴截面如图,则,∴.圆台高,∴.故选:D4.(2023·浙江)(多选)圆柱的侧面展开图是长4cm,宽2cm的矩形,则这个圆柱的体积可能是( )A. B.C. D.【答案】BD【解析】侧面展开图是长4cm,宽2cm的矩形,若圆柱的底面周长为4cm,则底面半径,,此时圆柱的体积若圆柱的底面周长为2cm,则底面半径,,此时圆柱的体积故选:BD考点二 表面积【例2】(2023辽宁)已知四棱台的上、下底面分别是边长为和的正方形,侧面均为腰长为的等腰梯形,则该四棱台的表面积为( )A. B.C. D.【答案】C【解析】设在正四棱台中,取侧面,则,,,如下图所示:分别过点、在侧面内作,,垂足分别为、,因为,,,所以,,,因为,,,故四边形为矩形,故,所以,,,因此,该四棱台的表面积为.故选:C.【一隅三反】1.(2023江苏无锡)为了给热爱朗读的师生提供一个安静独立的环境,某学校修建了若干“朗读亭”.如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,正六棱柱两条相对侧棱所在的轴截面为正方形,若正六棱锥与六棱柱的高的比值为1∶3,则正六棱锥与正六棱柱的侧面积之比为( )A. B. C. D.【答案】B【解析】由题意设正六边形的边长为a,设六棱柱的高为3b,六棱锥的高为b,正六棱柱的侧面积,正六棱锥的母线长为∴正六棱锥的侧面积,∵正六棱柱两条相对侧棱所在的轴截面为正方形,∴,∴∴,故选:B.2(2022上海徐汇)若圆台的高是4,母线长为5,侧面积是,则圆台的上、下底面的面积之和是______.【答案】【解析】设上下底的半径分别为,,则母线,高,构成一个直角三角形,母线为斜边5,高为直角边4,由勾股定理得,即,圆台的侧面积,所以,则,所以圆台的上、下底面的面积之和是.故答案为:.考点三 直线、平面平行【例3】(2022山东聊城)由四棱柱截去三棱锥后得到的几何体如图所示,四边形为平行四边形,O为与的交点.(1)求证:∥平面;(2)求证:平面∥平面;(3)设平面与底面的交线为l,求证:.【答案】证明见解析【解析】(1)取的中点,连接,∵是四棱柱,∴,∴四边形为平行四边形,∴,又平面平面,∴平面.(2)∵,∴四边形是平行四边形,∴,∵平面平面,∴平面,由(1)得平面且,平面,∴平面平面.(3)由(2)得:平面,又平面,平面平面,∴.【一隅三反】1.(2022青海海南)如图,四边形是矩形,平面,平面.(1)证明:平面平面.(2)若平面与平面的交线为,求证:【答案】(1)证明见解析(2)证明见解析【解析】(1)证明:因为平面,平面,所以,又因为平面,平面,所以平面,在矩形中,,平面,平面,所以平面,又,所以平面平面;(2)证明:,平面,又,.2.(2022秋·贵州)正的边长为2,是边上的高,E,F分别是和的中点(如图甲).现将沿翻成直二面角(如图乙).在图乙中:(1)求证:平面;(2)求点到平面的距离.【答案】(1)证明见解析(2)【解析】(1)在△ABC中,因为E,F分别是AC,BC的中点,所以.又平面DEF,平面DEF,所以平面DEF.(2)在题图甲中,因为是正的高,所以,所以在题图乙中,,所以是二面角的平面角,又二面角是直二面角,所以,由于平面,所以平面.因为是的中点,所以三棱锥的高为.三角形的面积是,又是的中点,所以,所以.因为,所以.设点到平面的距离为,则,解得,所以点到平面的距离为.3.(2022秋·上海)(1)叙述两个平面平行的判定定理,并证明;(2)如图,正方体中,分别为的中点,求证:平面平面.【答案】(1)见解析;(2)见解析.【解析】(1)面面平行的判定定理:如果一个平面内两条相交直线与另一个平面平行,那么这两个平面平行,即,,,,,证明:假设,∵,,,∴,同理可得,,∴,与矛盾,所以不成立,所以.(2)取中点,连接,,,∵为正方体,,为,中点,∴,,,,∴四边形,为平行四边形,,,∵平面,平面,平面,平面,∴∥平面,∥平面,∵平面,平面,,∴平面∥平面.考点四 直线、平面垂直【例4】(2023浙江丽水)(多选)已知正方体是中点,则( )A.面 B.C. D.平面【答案】BC【解析】与平面相交于点,故选项A错误;,面面面,故选项B正确;连接,为等边三角形,为中点,,,则故选项C正确;由于,故不垂直于,不垂直于平面,故选项D错误.故选:BC.【一隅三反】1.(2023·海南)(多选)在长方体中,,,则下列线段与垂直的有( )A. B. C. D.【答案】ABD【解析】如图所示,因为,所以侧面是正方形,所以,长方体中,平面,平面, ,平面,,故平面,平面, ,A选项正确;同理平面,平面,,B选项正确;,所以四边形为正方形,所以,D选项正确;易知,交于长方体的中心O,,在中,可得,故,所以不与垂直,C选项错误.故选:ABD2.(2022秋·河北唐山)(多选)如图,在长方体中,M,N分别为棱,的中点,则下列判断正确的是( ).A.直线与是异面直线 B.平面C.平面 D.【答案】AB【解析】由与平面相交于点,且不在直线上,平面,故与是异面直线,故A正确;根据题意知为长方体,故平面,故B正确;取的中点为Q,连接,且,故四边形为平行四边形,故,又与平面相交于点A,故与平面不平行,即与平面不平行,故C错误;因为,且与不垂直,所以与也不垂直,故D错误.故选:AB.3.(2022秋·青海海东)如图,已知四棱锥的底面ABCD是菱形,,点E为PC的中点.(1)求证:平面BDE;(2)求证:平面平面PAC.【答案】(1)证明见解析(2)证明见解析【解析】(1)连接AC交BD于O点,连接EO,∵底面ABCD是菱形,O为AC的中点,∵点E为PC的中点,, ∵平面BDE,且平面BDE,∴平面BDE;(2)∵底面ABCD是菱形,∴, ∵,,平面PAC,平面PAC, ∴平面PAC, 又平面PBD,∴平面平面PAC.考点五 空间角【例5】(2022·浙江)(多选)《九章算术·商功》:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳌臑.”其中,阳马是底面为矩形,且有一条侧棱与底面垂直的四棱锥.如图,在阳马中底面是边长为1的正方形,,侧棱垂直于底面,则( )A.直线与所成的角为60°B.直线与所成的角为60°C.直线与平面所成的角为30°D.直线与平面所成的角为30°【答案】AD【解析】连接,由底面,所以,由,是边长为1的正方形,所以,,对A,由底面,所以,又,所以平面,由∥,所以直线与所成的角为直线与所成的角,,所以,故A正确;对B,由是边长为1的正方形,所以,由底面,所以,又,所以平面,所以,故B错误;对C,由底面,所以直线与平面所成的角为,由,所以,故C错误;对D,由底面,所以,又,,所以,直线与平面所成的角为,由,所以,所以,故D正确.故选:AD【一隅三反】1.(2022春·广西桂林·高二校考期中)如图,在四棱锥中,PD⊥底面ABCD,四边形ABCD为正方形,且,G为△ABC的重心,则PG与底面ABCD所成的角的正弦值等于( )A. B. C. D.【答案】C【解析】连接BD交于,四边形ABCD为正方形,则为中点,∵G为△ABC的重心,则G在BD上,且,∴,∵PD⊥底面ABCD,∴为PG与底面ABCD所成的角,面ABCD,则,∴,∴.故选:C2.(2022上海黄浦)过正方形ABCD之顶点A作平面,若,则平面与平面所成的锐二面角的度数为________.【答案】【解析】根据已知条件可将四棱锥补成正方体如图所示:连接CE,则平面CDP和平面CPE为同一个平面,由题可知平面,平面,∴,,又平面和平面,平面,平面,∴为平面和平面所成的锐二面角的平面角,大小为.故答案为:.3.(2022秋·四川达州)如图,在四棱锥中,面,,,点分别为的中点,,.(1)证明:直线平面;(2)求二面角的余弦值.【答案】(1)证明见解析(2).【解析】(1)证明:点分别为的中点,,,,平面,平面,平面.(2)解:,,连接,由得,,,所以,,底面,底面,,是平面内两相交直线,平面,平面,二面角得平面角为,,,,所以二面角的余弦值为,即二面角的余弦值为.考点六 空间距离【例6-1】(2022秋·重庆南岸·高二重庆市第十一中学校校考期末)如图,在直三棱柱中,是等边三角形,,是棱的中点.求点到平面的距离等于_______【答案】【解析】因为是直三棱柱,所以平面,而平面,所以,因为是棱的中点,所以,由勾股定理可得:,,因为是等边三角形,是棱的中点.,所以,所以,因为,所以,因此,因为平面,平面,所以平面平面,因为平面平面,,平面,所以平面,设点到平面的距离为,由,故答案为:【一隅三反】1.(2022秋·上海黄浦)的三边长分别为3、4、5,为平面外一点,它到三边的距离都等于2,则到平面的距离是________.【答案】【解析】如图,,则为直角三角形,作平面于,于,于,于,连接,由题可知,故,由平面,平面,所以,又,平面,平面,平面,平面,,同理,故O是的内切圆圆心,设其半径为,则,所以,所以.故答案为:.2.(2022秋·上海黄浦)若正四棱柱的底面边长为,与底面成角,则到底面的距离为__________.【答案】【解析】∵正四棱柱,∴平面平面,平面,平面,到底面的距离为正四棱柱的高∵正四棱柱的底面边长为,与底面成角,故答案为:.3.(2023重庆巫山)如图,在四棱锥中,底面是菱形,,平面平面,,,PD的中点为F.(1)求证:平面;(2)求直线到面的距离.【答案】(1)证明见解析(2).【解析】(1)连接BD交AC于O,连接FO,∵F为AD的中点,O为BD的中点,则,∵平面ACF,平面ACF,∴平面ACF.(2)因为平面平面ABCD,平面平面,,平面,所以平面ABCD.由于平面ACF,则PB到平面ACF的距离,即P到平面ACF的距离.又因为F为PD的中点,点P到平面ACF的距离与点D到平面ACF的距离相等.取AD的中点E,连接EF,CE, 则,因为平面ABCD,所以平面ABCD,因为平面,所以,因为菱形且,,所以,,则,,,,设点D到平面ACF的距离为,由得即直线PB到平面ACF的距离为.4.(2023浙江)已知正方体的棱长均为1.(1)求到平面的距离;(2)求平面与平面之间的距离.【答案】(1);(2).【解析】(1)如图: 设到平面的距离为,正方体的棱长均为1,且面.,. .(2) 平面,平面.故平面平面.到平面的距离等于平面与平面之间的距离,设为. 即..
第8章 立体几何初步 重难点归纳总结考点一 体积【例1】(2023浙江丽水)已知一个圆锥的底面半径为1,其侧面积是底面积2倍,则圆锥的体积为( )A. B. C. D.【一隅三反】1.(2023·江西)陀螺是中国民间最早的娱乐工具之一,也称陀罗.图1是一种木陀螺,可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图2所示,其中分别是上、下底面圆的圆心,且,底面圆的半径为2,则该陀螺的体积是( )A. B. C. D.2.(2022秋·吉林)如图是一个棱长为2的正方体被过棱、的中点、,顶点和过点顶点、的两个截面截去两个角后所得的几何体,则该几何体的体积为( )A.5 B.6 C.7 D.83.(2023·河南信阳)已知圆台上下底面半径之比为1:2,母线与底面所成的角为60°,其侧面面积为,则该圆台的体积为( )A. B. C. D.4.(2023·浙江)(多选)圆柱的侧面展开图是长4cm,宽2cm的矩形,则这个圆柱的体积可能是( )A. B.C. D.考点二 表面积【例2】(2023辽宁)已知四棱台的上、下底面分别是边长为和的正方形,侧面均为腰长为的等腰梯形,则该四棱台的表面积为( )A. B.C. D.【一隅三反】1.(2023江苏无锡)为了给热爱朗读的师生提供一个安静独立的环境,某学校修建了若干“朗读亭”.如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,正六棱柱两条相对侧棱所在的轴截面为正方形,若正六棱锥与六棱柱的高的比值为1∶3,则正六棱锥与正六棱柱的侧面积之比为( )A. B. C. D.2(2022上海徐汇)若圆台的高是4,母线长为5,侧面积是,则圆台的上、下底面的面积之和是______.考点三 直线、平面平行【例3】(2022山东聊城)由四棱柱截去三棱锥后得到的几何体如图所示,四边形为平行四边形,O为与的交点.(1)求证:∥平面;(2)求证:平面∥平面;(3)设平面与底面的交线为l,求证:.【一隅三反】1.(2022青海海南)如图,四边形是矩形,平面,平面.(1)证明:平面平面.(2)若平面与平面的交线为,求证:2.(2022秋·贵州)正的边长为2,是边上的高,E,F分别是和的中点(如图甲).现将沿翻成直二面角(如图乙).在图乙中:(1)求证:平面;(2)求点到平面的距离.3.(2022秋·上海)(1)叙述两个平面平行的判定定理,并证明;(2)如图,正方体中,分别为的中点,求证:平面平面.考点四 直线、平面垂直【例4】(2023浙江丽水)(多选)已知正方体是中点,则( )A.面 B.C. D.平面【一隅三反】1.(2023·海南)(多选)在长方体中,,,则下列线段与垂直的有( )A. B. C. D.2.(2022秋·河北唐山)(多选)如图,在长方体中,M,N分别为棱,的中点,则下列判断正确的是( ).A.直线与是异面直线 B.平面C.平面 D.3.(2022秋·青海海东)如图,已知四棱锥的底面ABCD是菱形,,点E为PC的中点.(1)求证:平面BDE;(2)求证:平面平面PAC.考点五 空间角【例5】(2022·浙江)(多选)《九章算术·商功》:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳌臑.”其中,阳马是底面为矩形,且有一条侧棱与底面垂直的四棱锥.如图,在阳马中底面是边长为1的正方形,,侧棱垂直于底面,则( )A.直线与所成的角为60°B.直线与所成的角为60°C.直线与平面所成的角为30°D.直线与平面所成的角为30°【一隅三反】1.(2022春·广西桂林·高二校考期中)如图,在四棱锥中,PD⊥底面ABCD,四边形ABCD为正方形,且,G为△ABC的重心,则PG与底面ABCD所成的角的正弦值等于( )A. B. C. D.2.(2022上海黄浦)过正方形ABCD之顶点A作平面,若,则平面与平面所成的锐二面角的度数为________.3.(2022秋·四川达州)如图,在四棱锥中,面,,,点分别为的中点,,.(1)证明:直线平面;(2)求二面角的余弦值.考点六 空间距离【例6-1】(2022秋·重庆南岸·高二重庆市第十一中学校校考期末)如图,在直三棱柱中,是等边三角形,,是棱的中点.求点到平面的距离等于_______【一隅三反】1.(2022秋·上海黄浦)的三边长分别为3、4、5,为平面外一点,它到三边的距离都等于2,则到平面的距离是________.2.(2022秋·上海黄浦)若正四棱柱的底面边长为,与底面成角,则到底面的距离为__________.3.(2023重庆巫山)如图,在四棱锥中,底面是菱形,,平面平面,,,PD的中点为F.(1)求证:平面;(2)求直线到面的距离.4.(2023浙江)已知正方体的棱长均为1.(1)求到平面的距离;(2)求平面与平面之间的距离. 第8章 立体几何初步 重难点归纳总结考点一 体积【例1】(2023浙江丽水)已知一个圆锥的底面半径为1,其侧面积是底面积2倍,则圆锥的体积为( )A. B. C. D.【答案】B【解析】设圆锥的母线为l,由题意得,解得,所以圆锥的高为,所以圆锥的体积为,故选:B【一隅三反】1.(2023·江西)陀螺是中国民间最早的娱乐工具之一,也称陀罗.图1是一种木陀螺,可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图2所示,其中分别是上、下底面圆的圆心,且,底面圆的半径为2,则该陀螺的体积是( )A. B. C. D.【答案】D【解析】已知底面圆的半径,由,则,故该陀螺的体积.故选:D.2.(2022秋·吉林)如图是一个棱长为2的正方体被过棱、的中点、,顶点和过点顶点、的两个截面截去两个角后所得的几何体,则该几何体的体积为( )A.5 B.6 C.7 D.8【答案】C【解析】如图将正方体还原可得如下图形:则,,,所以该几何体的体积.故选:C3.(2023·河南信阳)已知圆台上下底面半径之比为1:2,母线与底面所成的角为60°,其侧面面积为,则该圆台的体积为( )A. B. C. D.【答案】D【解析】圆台轴截面如图,则,∴.圆台高,∴.故选:D4.(2023·浙江)(多选)圆柱的侧面展开图是长4cm,宽2cm的矩形,则这个圆柱的体积可能是( )A. B.C. D.【答案】BD【解析】侧面展开图是长4cm,宽2cm的矩形,若圆柱的底面周长为4cm,则底面半径,,此时圆柱的体积若圆柱的底面周长为2cm,则底面半径,,此时圆柱的体积故选:BD考点二 表面积【例2】(2023辽宁)已知四棱台的上、下底面分别是边长为和的正方形,侧面均为腰长为的等腰梯形,则该四棱台的表面积为( )A. B.C. D.【答案】C【解析】设在正四棱台中,取侧面,则,,,如下图所示:分别过点、在侧面内作,,垂足分别为、,因为,,,所以,,,因为,,,故四边形为矩形,故,所以,,,因此,该四棱台的表面积为.故选:C.【一隅三反】1.(2023江苏无锡)为了给热爱朗读的师生提供一个安静独立的环境,某学校修建了若干“朗读亭”.如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,正六棱柱两条相对侧棱所在的轴截面为正方形,若正六棱锥与六棱柱的高的比值为1∶3,则正六棱锥与正六棱柱的侧面积之比为( )A. B. C. D.【答案】B【解析】由题意设正六边形的边长为a,设六棱柱的高为3b,六棱锥的高为b,正六棱柱的侧面积,正六棱锥的母线长为∴正六棱锥的侧面积,∵正六棱柱两条相对侧棱所在的轴截面为正方形,∴,∴∴,故选:B.2(2022上海徐汇)若圆台的高是4,母线长为5,侧面积是,则圆台的上、下底面的面积之和是______.【答案】【解析】设上下底的半径分别为,,则母线,高,构成一个直角三角形,母线为斜边5,高为直角边4,由勾股定理得,即,圆台的侧面积,所以,则,所以圆台的上、下底面的面积之和是.故答案为:.考点三 直线、平面平行【例3】(2022山东聊城)由四棱柱截去三棱锥后得到的几何体如图所示,四边形为平行四边形,O为与的交点.(1)求证:∥平面;(2)求证:平面∥平面;(3)设平面与底面的交线为l,求证:.【答案】证明见解析【解析】(1)取的中点,连接,∵是四棱柱,∴,∴四边形为平行四边形,∴,又平面平面,∴平面.(2)∵,∴四边形是平行四边形,∴,∵平面平面,∴平面,由(1)得平面且,平面,∴平面平面.(3)由(2)得:平面,又平面,平面平面,∴.【一隅三反】1.(2022青海海南)如图,四边形是矩形,平面,平面.(1)证明:平面平面.(2)若平面与平面的交线为,求证:【答案】(1)证明见解析(2)证明见解析【解析】(1)证明:因为平面,平面,所以,又因为平面,平面,所以平面,在矩形中,,平面,平面,所以平面,又,所以平面平面;(2)证明:,平面,又,.2.(2022秋·贵州)正的边长为2,是边上的高,E,F分别是和的中点(如图甲).现将沿翻成直二面角(如图乙).在图乙中:(1)求证:平面;(2)求点到平面的距离.【答案】(1)证明见解析(2)【解析】(1)在△ABC中,因为E,F分别是AC,BC的中点,所以.又平面DEF,平面DEF,所以平面DEF.(2)在题图甲中,因为是正的高,所以,所以在题图乙中,,所以是二面角的平面角,又二面角是直二面角,所以,由于平面,所以平面.因为是的中点,所以三棱锥的高为.三角形的面积是,又是的中点,所以,所以.因为,所以.设点到平面的距离为,则,解得,所以点到平面的距离为.3.(2022秋·上海)(1)叙述两个平面平行的判定定理,并证明;(2)如图,正方体中,分别为的中点,求证:平面平面.【答案】(1)见解析;(2)见解析.【解析】(1)面面平行的判定定理:如果一个平面内两条相交直线与另一个平面平行,那么这两个平面平行,即,,,,,证明:假设,∵,,,∴,同理可得,,∴,与矛盾,所以不成立,所以.(2)取中点,连接,,,∵为正方体,,为,中点,∴,,,,∴四边形,为平行四边形,,,∵平面,平面,平面,平面,∴∥平面,∥平面,∵平面,平面,,∴平面∥平面.考点四 直线、平面垂直【例4】(2023浙江丽水)(多选)已知正方体是中点,则( )A.面 B.C. D.平面【答案】BC【解析】与平面相交于点,故选项A错误;,面面面,故选项B正确;连接,为等边三角形,为中点,,,则故选项C正确;由于,故不垂直于,不垂直于平面,故选项D错误.故选:BC.【一隅三反】1.(2023·海南)(多选)在长方体中,,,则下列线段与垂直的有( )A. B. C. D.【答案】ABD【解析】如图所示,因为,所以侧面是正方形,所以,长方体中,平面,平面, ,平面,,故平面,平面, ,A选项正确;同理平面,平面,,B选项正确;,所以四边形为正方形,所以,D选项正确;易知,交于长方体的中心O,,在中,可得,故,所以不与垂直,C选项错误.故选:ABD2.(2022秋·河北唐山)(多选)如图,在长方体中,M,N分别为棱,的中点,则下列判断正确的是( ).A.直线与是异面直线 B.平面C.平面 D.【答案】AB【解析】由与平面相交于点,且不在直线上,平面,故与是异面直线,故A正确;根据题意知为长方体,故平面,故B正确;取的中点为Q,连接,且,故四边形为平行四边形,故,又与平面相交于点A,故与平面不平行,即与平面不平行,故C错误;因为,且与不垂直,所以与也不垂直,故D错误.故选:AB.3.(2022秋·青海海东)如图,已知四棱锥的底面ABCD是菱形,,点E为PC的中点.(1)求证:平面BDE;(2)求证:平面平面PAC.【答案】(1)证明见解析(2)证明见解析【解析】(1)连接AC交BD于O点,连接EO,∵底面ABCD是菱形,O为AC的中点,∵点E为PC的中点,, ∵平面BDE,且平面BDE,∴平面BDE;(2)∵底面ABCD是菱形,∴, ∵,,平面PAC,平面PAC, ∴平面PAC, 又平面PBD,∴平面平面PAC.考点五 空间角【例5】(2022·浙江)(多选)《九章算术·商功》:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳌臑.”其中,阳马是底面为矩形,且有一条侧棱与底面垂直的四棱锥.如图,在阳马中底面是边长为1的正方形,,侧棱垂直于底面,则( )A.直线与所成的角为60°B.直线与所成的角为60°C.直线与平面所成的角为30°D.直线与平面所成的角为30°【答案】AD【解析】连接,由底面,所以,由,是边长为1的正方形,所以,,对A,由底面,所以,又,所以平面,由∥,所以直线与所成的角为直线与所成的角,,所以,故A正确;对B,由是边长为1的正方形,所以,由底面,所以,又,所以平面,所以,故B错误;对C,由底面,所以直线与平面所成的角为,由,所以,故C错误;对D,由底面,所以,又,,所以,直线与平面所成的角为,由,所以,所以,故D正确.故选:AD【一隅三反】1.(2022春·广西桂林·高二校考期中)如图,在四棱锥中,PD⊥底面ABCD,四边形ABCD为正方形,且,G为△ABC的重心,则PG与底面ABCD所成的角的正弦值等于( )A. B. C. D.【答案】C【解析】连接BD交于,四边形ABCD为正方形,则为中点,∵G为△ABC的重心,则G在BD上,且,∴,∵PD⊥底面ABCD,∴为PG与底面ABCD所成的角,面ABCD,则,∴,∴.故选:C2.(2022上海黄浦)过正方形ABCD之顶点A作平面,若,则平面与平面所成的锐二面角的度数为________.【答案】【解析】根据已知条件可将四棱锥补成正方体如图所示:连接CE,则平面CDP和平面CPE为同一个平面,由题可知平面,平面,∴,,又平面和平面,平面,平面,∴为平面和平面所成的锐二面角的平面角,大小为.故答案为:.3.(2022秋·四川达州)如图,在四棱锥中,面,,,点分别为的中点,,.(1)证明:直线平面;(2)求二面角的余弦值.【答案】(1)证明见解析(2).【解析】(1)证明:点分别为的中点,,,,平面,平面,平面.(2)解:,,连接,由得,,,所以,,底面,底面,,是平面内两相交直线,平面,平面,二面角得平面角为,,,,所以二面角的余弦值为,即二面角的余弦值为.考点六 空间距离【例6-1】(2022秋·重庆南岸·高二重庆市第十一中学校校考期末)如图,在直三棱柱中,是等边三角形,,是棱的中点.求点到平面的距离等于_______【答案】【解析】因为是直三棱柱,所以平面,而平面,所以,因为是棱的中点,所以,由勾股定理可得:,,因为是等边三角形,是棱的中点.,所以,所以,因为,所以,因此,因为平面,平面,所以平面平面,因为平面平面,,平面,所以平面,设点到平面的距离为,由,故答案为:【一隅三反】1.(2022秋·上海黄浦)的三边长分别为3、4、5,为平面外一点,它到三边的距离都等于2,则到平面的距离是________.【答案】【解析】如图,,则为直角三角形,作平面于,于,于,于,连接,由题可知,故,由平面,平面,所以,又,平面,平面,平面,平面,,同理,故O是的内切圆圆心,设其半径为,则,所以,所以.故答案为:.2.(2022秋·上海黄浦)若正四棱柱的底面边长为,与底面成角,则到底面的距离为__________.【答案】【解析】∵正四棱柱,∴平面平面,平面,平面,到底面的距离为正四棱柱的高∵正四棱柱的底面边长为,与底面成角,故答案为:.3.(2023重庆巫山)如图,在四棱锥中,底面是菱形,,平面平面,,,PD的中点为F.(1)求证:平面;(2)求直线到面的距离.【答案】(1)证明见解析(2).【解析】(1)连接BD交AC于O,连接FO,∵F为AD的中点,O为BD的中点,则,∵平面ACF,平面ACF,∴平面ACF.(2)因为平面平面ABCD,平面平面,,平面,所以平面ABCD.由于平面ACF,则PB到平面ACF的距离,即P到平面ACF的距离.又因为F为PD的中点,点P到平面ACF的距离与点D到平面ACF的距离相等.取AD的中点E,连接EF,CE, 则,因为平面ABCD,所以平面ABCD,因为平面,所以,因为菱形且,,所以,,则,,,,设点D到平面ACF的距离为,由得即直线PB到平面ACF的距离为.4.(2023浙江)已知正方体的棱长均为1.(1)求到平面的距离;(2)求平面与平面之间的距离.【答案】(1);(2).【解析】(1)如图: 设到平面的距离为,正方体的棱长均为1,且面.,. .(2) 平面,平面.故平面平面.到平面的距离等于平面与平面之间的距离,设为. 即..
相关资料
更多









