





还剩29页未读,
继续阅读
所属成套资源:全套北师大版初中八年级数学上册素养综合检测课件
成套系列资料,整套一键下载
北师大版初中八年级数学上册第一章勾股定理素养综合检测课件
展开
这是一份北师大版初中八年级数学上册第一章勾股定理素养综合检测课件,共37页。
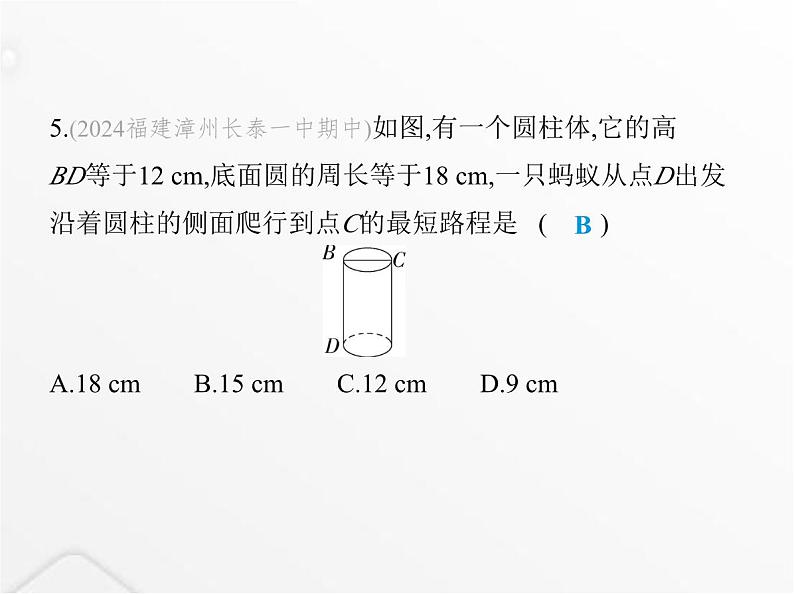
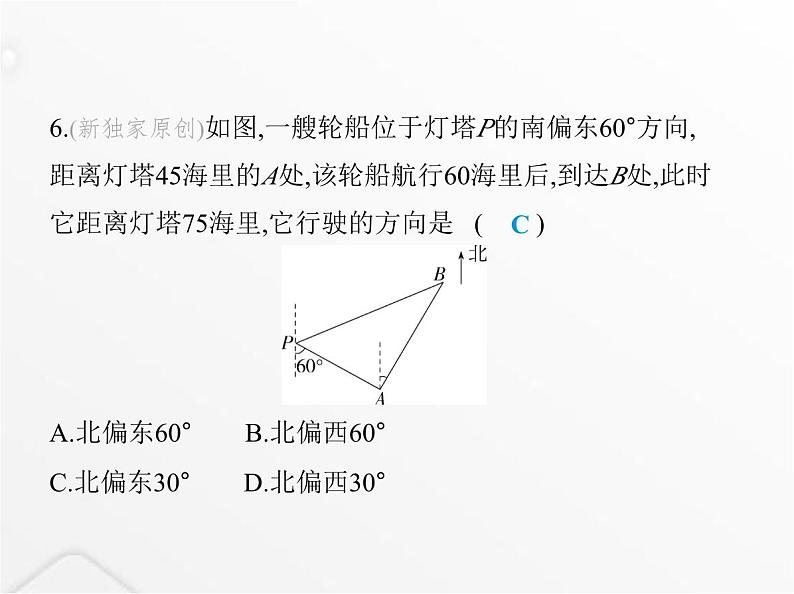
第一章 素养综合检测(满分100分, 限时60分钟)一、选择题(每小题3分,共30分)1.(2024广东佛山梁开中学期中)下列各组数中,是勾股数的 是 ( )A.6,8,12 B.0.6,0.8,1 C.8,15,16 D.9,12,15 D解析 选项A,∵62+82≠122,∴6,8,12不是一组勾股数,本选项 不符合题意;选项B,∵0.6,0.8不是正整数,∴0.6,0.8,1不是一组勾股数,本选项不符合题意;选项C,∵82+152≠162,∴8,15,16不是一组勾股数,本选项不符合题意;选项D,∵92+122=152,∴9,12,15是一组勾股数,本选项符合题意.故选D.2.如图,在Rt△ABC中,斜边BC=10,则AB2+AC2=( ) A.10 B.20 C.50 D.100 D解析 在Rt△ABC中,AB2+AC2=BC2=102=100,故选D.3.(2022贵州贵阳中考改编)如图,“赵爽弦图”是由四个全 等的直角三角形与中间的一个小正方形拼成的大正方形,若 图中的直角三角形的斜边和一条直角边的长分别为5和3,则 中间小正方形的周长是( ) A.4 B.8 C.12 D.16A解析 ∵52-32=16=42,∴题图中的直角三角形的另一条直角 边的长为4,则中间小正方形的周长是4×(4-3)=4.4.直角三角形的两直角边长分别为5 cm和12 cm,则其斜边上 的高为 ( )A.6 cm B.8 cm C. cm D. cmD5.(2024福建漳州长泰一中期中)如图,有一个圆柱体,它的高 BD等于12 cm,底面圆的周长等于18 cm,一只蚂蚁从点D出发 沿着圆柱的侧面爬行到点C的最短路程是 ( ) A.18 cm B.15 cm C.12 cm D.9 cm B解析 将圆柱的侧面展开,如图所示:由于底面圆的周长等于18 cm,则AD=18× =9 cm.又∵BD=AC=12 cm,∴DC2=AD2+AC2=92+122=225,∴DC=15 cm.故蚂蚁从点D出发沿着圆柱的侧面爬行到点C的最短路程为 15 cm.故答案为B.6.(新独家原创)如图,一艘轮船位于灯塔P的南偏东60°方向, 距离灯塔45海里的A处,该轮船航行60海里后,到达B处,此时 它距离灯塔75海里,它行驶的方向是 ( ) A.北偏东60° B.北偏西60°C.北偏东30° D.北偏西30°C解析 如图,由题意得PA=45海里,AB=60海里,PB=75海里.∵PA2+AB2=452+602=752=PB2,∴△PAB是直角三角形,∠PAB=90°,∵PC∥AD,∴∠CPA=∠PAD=60°,∴∠DAB=∠PAB-∠PAD=30°,∴轮船行驶的方向是北偏东30°.故选C. 7.(2023山东临沂期中)如图,正方形ABCD是由9个边长为1的 小正方形组成的,点E,F均在格点(每个小正方形的顶点都是 格点)上,连接AE,AF,则∠EAF的度数是 ( )A.35° B.40° C.45° D.50° C解析 如图,连接EF,∵AE2=22+12=5,EF2=22+12=5,AF2=32+12=10,∴AE2+EF2=AF2,AE=EF,∴△AEF是等腰直角三角形,∴∠EAF=45°.故选C. 8.(2024吉林长春实验学校期中)如图,有一个无盖的长方体 盒子,长方体的底面是边长为6的正方形,侧面都是长为13的 长方形.点D是BC的中点,在长方体下底面的A点处有一只蚂 蚁,它想吃到上底面点D处的蜂蜜,则沿着表面需要爬行的最 短路程是n,则n2的值为 ( ) A.292 B.250 C.370 D.205 B解析 将棱柱侧面展开,如图所示. ∵棱柱的底面是边长为6的正方形,侧面都是长为13的长方 形,点D是BC的中点,∴BD=3,∴n2=AD2=(3+6)2+132=250,故选B.9.(2023浙江宁波期末)勾股定理是我国的伟大数学发明之一.如图,以Rt△ABC的各边为边向外作正方形,再把较小的两 个正方形放入最大的正方形中,三个阴影部分的面积分别为 S1=1,S2=2,S3=3,则两个较小正方形重叠部分(四边形DEFG)的 面积为 ( ) A.4 B.5 C.5.5 D.6D解析 设直角三角形的斜边长为c,较长直角边长为a,较短直 角边长为b,由勾股定理得c2=a2+b2,∴c2-a2-b2=0,∴S阴影=c2-a2-(b2-S四边形DEFG)=c2-a2-b2+S四边形DEFG=S四边形DEFG,∴S四边形DEFG=S1+S2+S3,∵S1=1,S2=2,S3=3,∴S四边形DEFG=1+2+3=6.故选D.10.(2023河南南阳期末)如图,长方形ABCD中,AD=BC=6,AB= CD=10,点E为线段DC上的一个动点,将△ADE沿AE折叠得 到△AD'E,连接D'B,当△AD'B为直角三角形时,DE的长为( ) A.1 B.2C.1或 D.2或9B解析 ∵△ADE沿AE折叠得到△AD'E,∴∠AD'E=∠ADE=90°,D'E=DE,AD'=AD=6.∵△AD'B是直角三角形,点E在线段DC上,∴∠AD'B=90°,∴E、D'、B三点共线,∴S△ABE= AB·AD= BE·AD',又AB=10,∴ ×10×6= BE×6,∴BE=10.在Rt△AD'B中,BD'2=AB2-AD'2=102-62=64,∴BD'=8,∴DE=D'E=BE-BD'=10-8=2,故选B.二、填空题(每小题4分,共24分)11.判断由线段a,b,c组成的三角形是不是直角三角形:a=10,b =12,c=15.解:因为102+122=100+144=244,152=225,所以102+122≠152.根据勾股定理的逆定理,知这个三角形 直角三角形.(填“是”或“不是”)不是12.如图,从电线杆上离地面12 m的点C处向地面拉一条长为 13 m的钢缆,则地面钢缆固定点A到电线杆底部B的距离为 m. 5解析 在Rt△ABC中,BC=12 m,AC=13 m,∴AB2=AC2-BC2=132-122=25,∴AB=5 m.13.(风吹树折模型)(2022河南灵宝月考)由于台风的影响,一 棵树在折断前不包括树根的长度是16 m,折断后树顶落在离 树干底部8 m处,则这棵树在离地面 m处折断.6解析 设这棵树在离地面x m处折断,如图,∵BC=8 m,AB=x m,∴AC=(16-x)m,在直角三角形ABC中,根据勾股定理得x2+82=(16-x)2,解得x=6. 故答案为6. 14.如图,在△ABC中,AB=7 cm,AC=25 cm,BC=24 cm,动点P从 点A出发沿AB方向以1 cm/s的速度运动至点B,动点Q从点B 出发沿BC方向以6 cm/s的速度运动至点C,P、Q两点同时出 发,连接PQ.当动点P、Q运动2 s时,PQ= cm. 13解析 ∵AB=7 cm,AC=25 cm,BC=24 cm,∴AB2+BC2=625=AC2,∴△ABC是直角三角形,且∠B=90°.当动点P、Q运动2 s时,AP=1×2=2(cm),BQ=2×6=12(cm),∴BP=AB-AP=7-2=5(cm).在Rt△BPQ中,由勾股定理得PQ2=BP2+BQ2=52+122=169,∴PQ=13 cm.15.(勾股树模型)(2022四川成都向阳桥中学月考)若图中所有 的四边形都是正方形,所有的三角形都是直角三角形,其中最 大的正方形的面积为9 cm2,则图中所有的正方形的面积之和 为 cm2. 27解析 根据勾股定理可知所有的正方形的面积之和为3×9= 27 cm2.16.(2023山东青岛月考)如图,将一根20 cm长的细木棒放入 长、宽、高分别为4 cm、3 cm和12 cm的长方体无盖盒子 中,则细木棒露在盒外面的最短长度是 cm. 7解析 如图,由题意知盒子底面对角线长的平方=32+42=25,盒子的体对角线长的平方=25+122=169,∴盒子的体对角线长为13 cm.∵细木棒的长为20 cm,∴细木棒露在盒子外面的最短长度是20-13=7 cm,故答案为7. 三、解答题(共46分)17.(2024陕西咸阳彩虹学校期中)(8分)如图,正方形网格的每 个小方格的边长为1,△ABC的顶点在格点上.请判断△ABC 的形状,并说明理由. 解析 △ABC是直角三角形,理由如下:由题意可得AB2=42+22=20,AC2=32+42=25,BC2=12+22=5,∴AB2+BC2=20+5=25=AC2,∴△ABC是直角三角形.18.(情境题·现实生活)(2022山东枣庄四中月考)(8分)老师准 备测量一段河水的深度,他把一根竹竿插到离岸边1.5 m远的 水底,竹竿露出水面的部分刚好为0.5 m,把竹竿的顶端拉向 岸边,竿顶和岸边的水面刚好相齐,请你帮老师计算河水的深 度是多少米. 解析 设河水的深度为h米.由勾股定理得h2+1.52=(h+0.5)2,h2+2.25=h2+h+0.25,解得h=2.答:河水的深度为2米.19.(10分)如图所示的是用硬纸板做成的四个全等的直角三 角形(两直角边长分别是a、b,斜边长为c)和一个正方形(边 长为c).请你将它们拼成一个能验证勾股定理的图形.(1)画出拼成的图形的示意图.(2)用(1)中画出的图形验证勾股定理.解析 (1)如图.(答案不唯一) (2)∵大正方形的面积可以表示为(a+b)2,也可以表示为c2+4× ab,∴(a+b)2=c2+4× ab,即a2+b2+2ab=c2+2ab,∴a2+b2=c2,即直角三角形两直角边的平方和等于斜边的平方.20.(2023四川成都锦西中学月考)(10分)如图,等腰三角形 ABC的底边BC的长为8 cm,腰AB、AC的长为5 cm,一动点P 在底边上从点B向点C以0.25 cm/s的速度移动,当点P运动到 PA与腰垂直的位置时,求点P运动的时间. 解析 如图,作AD⊥BC,交BC于点D,∵BC=8 cm,∴BD=CD= BC=4 cm,∴AD2=AB2-BD2=9,∴AD=3 cm.分两种情况:①点P运动t秒后有PA⊥AC(如图1),BP=0.25t cm.∵AP2=PD2+AD2=PC2-AC2,∴PD2+32=(PD+4)2-52,∴PD=2.25 cm,∴BP=4-2.25=1.75 cm.∴1.75=0.25t,∴t=7.②点P运动t秒后有PA⊥AB(如图2),同理可证得PD=2.25 cm,∴BP=4+2.25=6.25 cm.∴6.25=0.25t,∴t=25. ∴点P运动的时间为7秒或25秒.21.(新考向·代数推理)(10分)已知n组正整数:第一组:3,4,5;第二组:8,6,10;第三组:15,8,17;第四组:24,10,26; 第五组:35,12,37;第六组:48,14,50;……(1)是否存在一组数符合上述规律,且其中一个数为71?若存 在,请写出这组数;若不存在,请说明理由.(2)以任意一个大于2的偶数为一条直角边的长,是否一定可 以画出一个直角三角形,使得该直角三角形的另两条边的长 都是正整数?若可以,请说明理由;若不可以,请举出反例.解析 (1)不存在一组数符合上述规律,且其中一个数为71. 理由如下:根据题意可知,第(m-1)组数为m2-1,2m,m2+1(m≥2,且m为整 数).若m2-1=71,则m2=72,此时m不符合题意;若2m=71,则m=35.5,此时m不符合题意;若m2+1=71,则m2=70,此时m不符合题意.所以不存在一组数符合上述规律,且其中一个数为71.(2)可以.理由如下:对于一组数:m2-1,2m,m2+1(m≥2,且m为整数).因为(m2-1)2+(2m)2=m4+2m2+1=(m2+1)2,所以若一个三角形三边长分别为m2-1,2m,m2+1(m≥2,且m为 整数),则该三角形为直角三角形.因为当m≥2,且m为整数时,2m表示任意一个大于2的偶数,m2- 1,m2+1均为正整数,所以以任意一个大于2的偶数为一条直角边的长,一定可以 画出一个直角三角形,使得该直角三角形的另两条边的长都 是正整数.
第一章 素养综合检测(满分100分, 限时60分钟)一、选择题(每小题3分,共30分)1.(2024广东佛山梁开中学期中)下列各组数中,是勾股数的 是 ( )A.6,8,12 B.0.6,0.8,1 C.8,15,16 D.9,12,15 D解析 选项A,∵62+82≠122,∴6,8,12不是一组勾股数,本选项 不符合题意;选项B,∵0.6,0.8不是正整数,∴0.6,0.8,1不是一组勾股数,本选项不符合题意;选项C,∵82+152≠162,∴8,15,16不是一组勾股数,本选项不符合题意;选项D,∵92+122=152,∴9,12,15是一组勾股数,本选项符合题意.故选D.2.如图,在Rt△ABC中,斜边BC=10,则AB2+AC2=( ) A.10 B.20 C.50 D.100 D解析 在Rt△ABC中,AB2+AC2=BC2=102=100,故选D.3.(2022贵州贵阳中考改编)如图,“赵爽弦图”是由四个全 等的直角三角形与中间的一个小正方形拼成的大正方形,若 图中的直角三角形的斜边和一条直角边的长分别为5和3,则 中间小正方形的周长是( ) A.4 B.8 C.12 D.16A解析 ∵52-32=16=42,∴题图中的直角三角形的另一条直角 边的长为4,则中间小正方形的周长是4×(4-3)=4.4.直角三角形的两直角边长分别为5 cm和12 cm,则其斜边上 的高为 ( )A.6 cm B.8 cm C. cm D. cmD5.(2024福建漳州长泰一中期中)如图,有一个圆柱体,它的高 BD等于12 cm,底面圆的周长等于18 cm,一只蚂蚁从点D出发 沿着圆柱的侧面爬行到点C的最短路程是 ( ) A.18 cm B.15 cm C.12 cm D.9 cm B解析 将圆柱的侧面展开,如图所示:由于底面圆的周长等于18 cm,则AD=18× =9 cm.又∵BD=AC=12 cm,∴DC2=AD2+AC2=92+122=225,∴DC=15 cm.故蚂蚁从点D出发沿着圆柱的侧面爬行到点C的最短路程为 15 cm.故答案为B.6.(新独家原创)如图,一艘轮船位于灯塔P的南偏东60°方向, 距离灯塔45海里的A处,该轮船航行60海里后,到达B处,此时 它距离灯塔75海里,它行驶的方向是 ( ) A.北偏东60° B.北偏西60°C.北偏东30° D.北偏西30°C解析 如图,由题意得PA=45海里,AB=60海里,PB=75海里.∵PA2+AB2=452+602=752=PB2,∴△PAB是直角三角形,∠PAB=90°,∵PC∥AD,∴∠CPA=∠PAD=60°,∴∠DAB=∠PAB-∠PAD=30°,∴轮船行驶的方向是北偏东30°.故选C. 7.(2023山东临沂期中)如图,正方形ABCD是由9个边长为1的 小正方形组成的,点E,F均在格点(每个小正方形的顶点都是 格点)上,连接AE,AF,则∠EAF的度数是 ( )A.35° B.40° C.45° D.50° C解析 如图,连接EF,∵AE2=22+12=5,EF2=22+12=5,AF2=32+12=10,∴AE2+EF2=AF2,AE=EF,∴△AEF是等腰直角三角形,∴∠EAF=45°.故选C. 8.(2024吉林长春实验学校期中)如图,有一个无盖的长方体 盒子,长方体的底面是边长为6的正方形,侧面都是长为13的 长方形.点D是BC的中点,在长方体下底面的A点处有一只蚂 蚁,它想吃到上底面点D处的蜂蜜,则沿着表面需要爬行的最 短路程是n,则n2的值为 ( ) A.292 B.250 C.370 D.205 B解析 将棱柱侧面展开,如图所示. ∵棱柱的底面是边长为6的正方形,侧面都是长为13的长方 形,点D是BC的中点,∴BD=3,∴n2=AD2=(3+6)2+132=250,故选B.9.(2023浙江宁波期末)勾股定理是我国的伟大数学发明之一.如图,以Rt△ABC的各边为边向外作正方形,再把较小的两 个正方形放入最大的正方形中,三个阴影部分的面积分别为 S1=1,S2=2,S3=3,则两个较小正方形重叠部分(四边形DEFG)的 面积为 ( ) A.4 B.5 C.5.5 D.6D解析 设直角三角形的斜边长为c,较长直角边长为a,较短直 角边长为b,由勾股定理得c2=a2+b2,∴c2-a2-b2=0,∴S阴影=c2-a2-(b2-S四边形DEFG)=c2-a2-b2+S四边形DEFG=S四边形DEFG,∴S四边形DEFG=S1+S2+S3,∵S1=1,S2=2,S3=3,∴S四边形DEFG=1+2+3=6.故选D.10.(2023河南南阳期末)如图,长方形ABCD中,AD=BC=6,AB= CD=10,点E为线段DC上的一个动点,将△ADE沿AE折叠得 到△AD'E,连接D'B,当△AD'B为直角三角形时,DE的长为( ) A.1 B.2C.1或 D.2或9B解析 ∵△ADE沿AE折叠得到△AD'E,∴∠AD'E=∠ADE=90°,D'E=DE,AD'=AD=6.∵△AD'B是直角三角形,点E在线段DC上,∴∠AD'B=90°,∴E、D'、B三点共线,∴S△ABE= AB·AD= BE·AD',又AB=10,∴ ×10×6= BE×6,∴BE=10.在Rt△AD'B中,BD'2=AB2-AD'2=102-62=64,∴BD'=8,∴DE=D'E=BE-BD'=10-8=2,故选B.二、填空题(每小题4分,共24分)11.判断由线段a,b,c组成的三角形是不是直角三角形:a=10,b =12,c=15.解:因为102+122=100+144=244,152=225,所以102+122≠152.根据勾股定理的逆定理,知这个三角形 直角三角形.(填“是”或“不是”)不是12.如图,从电线杆上离地面12 m的点C处向地面拉一条长为 13 m的钢缆,则地面钢缆固定点A到电线杆底部B的距离为 m. 5解析 在Rt△ABC中,BC=12 m,AC=13 m,∴AB2=AC2-BC2=132-122=25,∴AB=5 m.13.(风吹树折模型)(2022河南灵宝月考)由于台风的影响,一 棵树在折断前不包括树根的长度是16 m,折断后树顶落在离 树干底部8 m处,则这棵树在离地面 m处折断.6解析 设这棵树在离地面x m处折断,如图,∵BC=8 m,AB=x m,∴AC=(16-x)m,在直角三角形ABC中,根据勾股定理得x2+82=(16-x)2,解得x=6. 故答案为6. 14.如图,在△ABC中,AB=7 cm,AC=25 cm,BC=24 cm,动点P从 点A出发沿AB方向以1 cm/s的速度运动至点B,动点Q从点B 出发沿BC方向以6 cm/s的速度运动至点C,P、Q两点同时出 发,连接PQ.当动点P、Q运动2 s时,PQ= cm. 13解析 ∵AB=7 cm,AC=25 cm,BC=24 cm,∴AB2+BC2=625=AC2,∴△ABC是直角三角形,且∠B=90°.当动点P、Q运动2 s时,AP=1×2=2(cm),BQ=2×6=12(cm),∴BP=AB-AP=7-2=5(cm).在Rt△BPQ中,由勾股定理得PQ2=BP2+BQ2=52+122=169,∴PQ=13 cm.15.(勾股树模型)(2022四川成都向阳桥中学月考)若图中所有 的四边形都是正方形,所有的三角形都是直角三角形,其中最 大的正方形的面积为9 cm2,则图中所有的正方形的面积之和 为 cm2. 27解析 根据勾股定理可知所有的正方形的面积之和为3×9= 27 cm2.16.(2023山东青岛月考)如图,将一根20 cm长的细木棒放入 长、宽、高分别为4 cm、3 cm和12 cm的长方体无盖盒子 中,则细木棒露在盒外面的最短长度是 cm. 7解析 如图,由题意知盒子底面对角线长的平方=32+42=25,盒子的体对角线长的平方=25+122=169,∴盒子的体对角线长为13 cm.∵细木棒的长为20 cm,∴细木棒露在盒子外面的最短长度是20-13=7 cm,故答案为7. 三、解答题(共46分)17.(2024陕西咸阳彩虹学校期中)(8分)如图,正方形网格的每 个小方格的边长为1,△ABC的顶点在格点上.请判断△ABC 的形状,并说明理由. 解析 △ABC是直角三角形,理由如下:由题意可得AB2=42+22=20,AC2=32+42=25,BC2=12+22=5,∴AB2+BC2=20+5=25=AC2,∴△ABC是直角三角形.18.(情境题·现实生活)(2022山东枣庄四中月考)(8分)老师准 备测量一段河水的深度,他把一根竹竿插到离岸边1.5 m远的 水底,竹竿露出水面的部分刚好为0.5 m,把竹竿的顶端拉向 岸边,竿顶和岸边的水面刚好相齐,请你帮老师计算河水的深 度是多少米. 解析 设河水的深度为h米.由勾股定理得h2+1.52=(h+0.5)2,h2+2.25=h2+h+0.25,解得h=2.答:河水的深度为2米.19.(10分)如图所示的是用硬纸板做成的四个全等的直角三 角形(两直角边长分别是a、b,斜边长为c)和一个正方形(边 长为c).请你将它们拼成一个能验证勾股定理的图形.(1)画出拼成的图形的示意图.(2)用(1)中画出的图形验证勾股定理.解析 (1)如图.(答案不唯一) (2)∵大正方形的面积可以表示为(a+b)2,也可以表示为c2+4× ab,∴(a+b)2=c2+4× ab,即a2+b2+2ab=c2+2ab,∴a2+b2=c2,即直角三角形两直角边的平方和等于斜边的平方.20.(2023四川成都锦西中学月考)(10分)如图,等腰三角形 ABC的底边BC的长为8 cm,腰AB、AC的长为5 cm,一动点P 在底边上从点B向点C以0.25 cm/s的速度移动,当点P运动到 PA与腰垂直的位置时,求点P运动的时间. 解析 如图,作AD⊥BC,交BC于点D,∵BC=8 cm,∴BD=CD= BC=4 cm,∴AD2=AB2-BD2=9,∴AD=3 cm.分两种情况:①点P运动t秒后有PA⊥AC(如图1),BP=0.25t cm.∵AP2=PD2+AD2=PC2-AC2,∴PD2+32=(PD+4)2-52,∴PD=2.25 cm,∴BP=4-2.25=1.75 cm.∴1.75=0.25t,∴t=7.②点P运动t秒后有PA⊥AB(如图2),同理可证得PD=2.25 cm,∴BP=4+2.25=6.25 cm.∴6.25=0.25t,∴t=25. ∴点P运动的时间为7秒或25秒.21.(新考向·代数推理)(10分)已知n组正整数:第一组:3,4,5;第二组:8,6,10;第三组:15,8,17;第四组:24,10,26; 第五组:35,12,37;第六组:48,14,50;……(1)是否存在一组数符合上述规律,且其中一个数为71?若存 在,请写出这组数;若不存在,请说明理由.(2)以任意一个大于2的偶数为一条直角边的长,是否一定可 以画出一个直角三角形,使得该直角三角形的另两条边的长 都是正整数?若可以,请说明理由;若不可以,请举出反例.解析 (1)不存在一组数符合上述规律,且其中一个数为71. 理由如下:根据题意可知,第(m-1)组数为m2-1,2m,m2+1(m≥2,且m为整 数).若m2-1=71,则m2=72,此时m不符合题意;若2m=71,则m=35.5,此时m不符合题意;若m2+1=71,则m2=70,此时m不符合题意.所以不存在一组数符合上述规律,且其中一个数为71.(2)可以.理由如下:对于一组数:m2-1,2m,m2+1(m≥2,且m为整数).因为(m2-1)2+(2m)2=m4+2m2+1=(m2+1)2,所以若一个三角形三边长分别为m2-1,2m,m2+1(m≥2,且m为 整数),则该三角形为直角三角形.因为当m≥2,且m为整数时,2m表示任意一个大于2的偶数,m2- 1,m2+1均为正整数,所以以任意一个大于2的偶数为一条直角边的长,一定可以 画出一个直角三角形,使得该直角三角形的另两条边的长都 是正整数.
相关资料
更多









