






还剩30页未读,
继续阅读
所属成套资源:全套北师大版初中八年级数学上册素养综合检测课件
成套系列资料,整套一键下载
北师大版初中八年级数学上册第四章一次函数素养综合检测课件
展开
这是一份北师大版初中八年级数学上册第四章一次函数素养综合检测课件,共38页。
第四章 素养综合检测(满分100分, 限时60分钟)一、选择题(每小题3分,共30分)1.(2023山西太原段考)下列是正比例函数的是 ( )A.y= B.y= C.y=x2 D.y=x-3B解析 形如y=kx(k为常数,k≠0)的函数是正比例函数,故选B.2.(2023河南郑州期中)某数学气象小组为较直观地了解当地 某一天24 h的气温与时间的关系,可选择的比较好的表示方 法是 ( )A.列表法B.图象法C.关系式法D.以上三种方法均可 B解析 图象法满足“直观”的要求,故选B.3.(2019广西河池中考)函数y=x-2的图象不经过 ( )A.第一象限 B.第二象限C.第三象限 D.第四象限B解析 ∵k=1>0,b=-2<0,∴函数y=x-2的图象经过第一、三、 四象限,不经过第二象限.故选B.方法归纳 直线y=kx+b(k≠0)所在的位置与k,b的关系:k>0 时,直线必经过第一、三象限;k<0时,直线必经过第二、四象 限;b>0时,直线与y轴正半轴相交;b=0时,直线必过原点;b<0 时,直线与y轴负半轴相交.4.(2023安徽安庆期末)点A(-2,y1),B(-1,y2)都在直线y=-x+b上, 则y1与y2的大小关系为 ( )A.y1=y2 B.y1>y2C.y1y2.5.(2024江苏盐城景山中学期末)若直线y=kx+b经过点(1,3),则
关于x的方程kx+b=3的解是 ( )A.x=1 B.x=2C.x=3 D.x=4A解析 ∵直线y=kx+b经过点(1,3),∴当x=1时,y=kx+b=3,∴关于x的方程kx+b=3的解是x=1,故选A.6.(2024陕西西安模拟)在平面直角坐标系中,若点P(m,n)在第
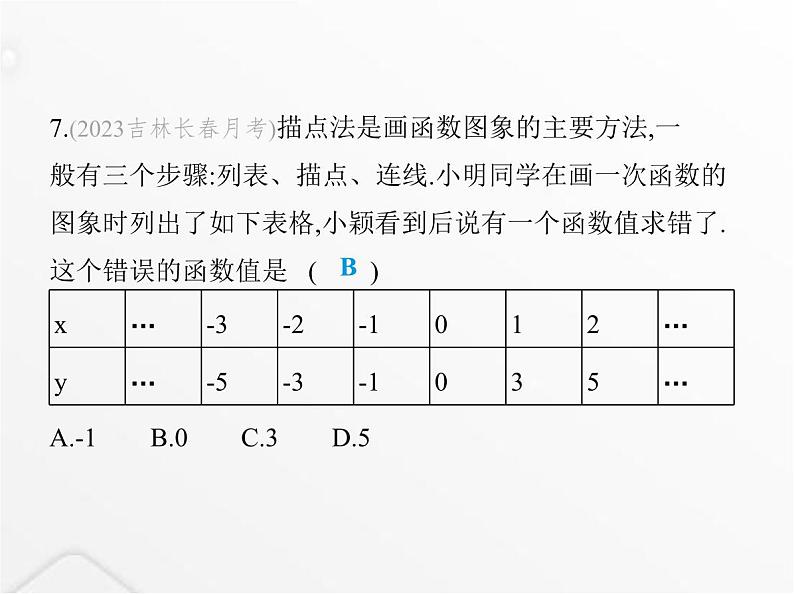
四象限,那么一次函数y=mx-n的图象大致是 ( ) D解析 ∵点P(m,n)在第四象限,∴m>0,n<0,∴-n>0,∴一次函数y=mx-n的图象经过第一、二、三象限,故选D.7.(2023吉林长春月考)描点法是画函数图象的主要方法,一
般有三个步骤:列表、描点、连线.小明同学在画一次函数的
图象时列出了如下表格,小颖看到后说有一个函数值求错了.
这个错误的函数值是 ( )A.-1 B.0 C.3 D.5B解析 根据表格数据可得当x值增大1时,函数值增大2,因此
在x=0时,表格中的函数值应为1,故这个错误的函数值是0.故
选B.8.(2023山东济南外国语学校期末)下列关于一次函数y=kx+b
(k<0,b>0)的说法,错误的是( )A.图象经过第一、二、四象限B.y随x的增大而减小C.图象与y轴交于点(0,b)D.当x>- 时,y>0 D解析 ∵y=kx+b(k<0,b>0),∴图象经过第一、二、四象限,A
正确;∵k<0,∴y随x的增大而减小,B正确;令x=0,则y=b,∴图象
与y轴的交点为(0,b),∴C正确;令y=0,则x=- ,当x>- 时,y<0,D不正确.故选D.9.(新考向·新定义试题)(2023江苏盐城期末)已知a,b,c分别是
Rt△ABC的三条边长,c为斜边长,∠C=90°,我们把关于x的形
如y= x+ 的一次函数称为“勾股一次函数”,若点P 在“勾股一次函数”的图象上,且Rt△ABC的面积是2,则c的
值是 ( )A.3 B.4 C.5 D.6 A解析 ∵点P 在“勾股一次函数”y= x+ 的图象上,∴ =- + ,即a-b=- c,∵a,b,c分别是Rt△ABC的三条边长,c为斜边长,∠C=90°,Rt△ABC的面积是2,∴ ab=2,即ab=4,a2+b2=c2,∴(a-b)2+2ab=c2,∴ +2×4=c2,解得c=3(负值舍去).故选A.10.(2024内蒙古包头期末)如图所示的是本地区一种产品30
天的销售情况的图象,图①是产品日销售量y(单位:件)与时间
t(单位:天)的函数关系图象,图②是一件产品的销售利润z(单
位:元)与时间t(单位:天)的函数关系图象,已知日销售利润=
日销售量×一件产品的销售利润.下列结论错误的是 ( )A.第24天的日销售量为200件B.第12天的日销售利润是1 950元C.第30天的日销售利润是5元D.第10天销售一件产品的利润是15元 C解析 根据题图①可知,当t=24时,y=200,即第24天的日销售
量为200件,故A正确,不符合题意;根据题图①,当0≤t≤24时,设y=kt+b(k≠0),将(24,200),(0,100)分别代入,得24k+b=200,b=100,∴k= ,∴y= t+100(0≤t≤24),同理可得z=-t+25(0≤t≤20),当t=12时,y= ×12+100=150,z=-12+25=13,∴第12天的日销售利润是150×13=1 950(元),故B正确,不符合题意;由题图①和题图②可知,第30天的日销售利润是150×5=750
(元),故C不正确,符合题意;当t=10时,z=-10+25=15,故D正确,
不符合题意.故选C.二、填空题(每小题4分,共24分)11.(2023福建宁德期中)已知函数y=-4x-3,当x= 时,函
数值为0.解析 依题意,得-4x-3=0,解得x=- .12.(2024广东广州期中)变量x,y有如下关系:①x+y=10;②y=
;③y=x-3;④y2=8x.其中y是x的函数的是 (填序号).①②③13.(2024广东茂名愉园中学期中)已知函数y=(k-3)x|k|-2+6是关
于x的一次函数,则k= .-3解析 ∵函数y=(k-3)x|k|-2+6是关于x的一次函数,∴|k|-2=1且k-3≠0,解得k=-3,故答案为-3.14.(新考向·开放性试题)(2022江苏宿迁中考)甲、乙两位同
学各给出某函数的一个特征,甲:“函数值y随自变量x的增大
而减小.”乙:“函数图象经过点(0,2).”请你写出一个同时
满足这两个特征的函数,其表达式是 . y=-x+2(答案不唯一)解析 ∵函数值y随自变量x的增大而减小,且该函数图象经
过点(0,2),∴该函数可为一次函数.设一次函数的表达式为y=kx+b(k≠0),则k<0,b=2.令k=-1,此时一次函数的表达式为y=-x+2.故答案为y=-x+2(答案不唯一).15.(2024重庆大渡口期末)一次函数y=k1x,y=k2x,y=k3x+b的图
象如图所示,则k1,k2,k3的大小关系为 .(用“<”连接) k10,k3>0,∵直线越陡,|k|越大,∴k30,∴y随x的增大而增大,∵点P(2,n1)和点Q(5,n2)在直线OA上,且2<5,∴n130,则选择方案一.
第四章 素养综合检测(满分100分, 限时60分钟)一、选择题(每小题3分,共30分)1.(2023山西太原段考)下列是正比例函数的是 ( )A.y= B.y= C.y=x2 D.y=x-3B解析 形如y=kx(k为常数,k≠0)的函数是正比例函数,故选B.2.(2023河南郑州期中)某数学气象小组为较直观地了解当地 某一天24 h的气温与时间的关系,可选择的比较好的表示方 法是 ( )A.列表法B.图象法C.关系式法D.以上三种方法均可 B解析 图象法满足“直观”的要求,故选B.3.(2019广西河池中考)函数y=x-2的图象不经过 ( )A.第一象限 B.第二象限C.第三象限 D.第四象限B解析 ∵k=1>0,b=-2<0,∴函数y=x-2的图象经过第一、三、 四象限,不经过第二象限.故选B.方法归纳 直线y=kx+b(k≠0)所在的位置与k,b的关系:k>0 时,直线必经过第一、三象限;k<0时,直线必经过第二、四象 限;b>0时,直线与y轴正半轴相交;b=0时,直线必过原点;b<0 时,直线与y轴负半轴相交.4.(2023安徽安庆期末)点A(-2,y1),B(-1,y2)都在直线y=-x+b上, 则y1与y2的大小关系为 ( )A.y1=y2 B.y1>y2C.y1
相关资料
更多









