初中数学6.3 角课文内容课件ppt

这是一份初中数学6.3 角课文内容课件ppt，共16页。PPT课件主要包含了学习目标，新课引入，角平分线，探究点1，获取新知，例题讲解，跟踪训练，角的三等分线，探究点2，角的计算等内容，欢迎下载使用。

1. 掌握角平分线、角的三等分线的意义及数量关系，能够用几何语言进行相关表述. (重点)2.能够综合应用角平分线与角的和差倍分关系进行角的推理计算，并能解答相关问题.(重点、难点)
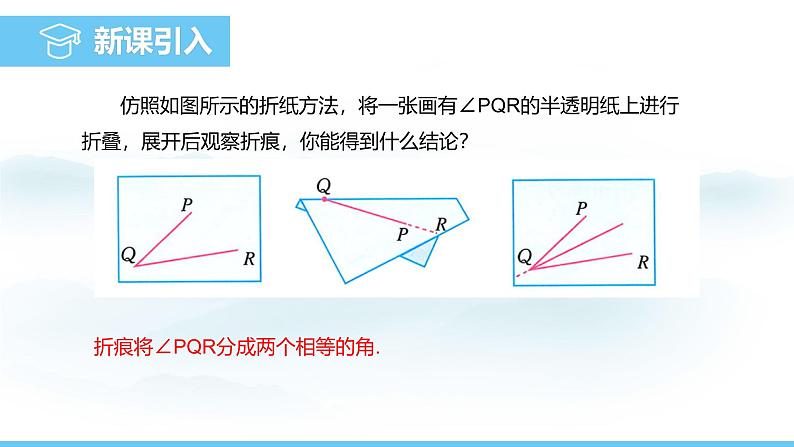
仿照如图所示的折纸方法，将一张画有∠PQR的半透明纸上进行折叠，展开后观察折痕，你能得到什么结论？
折痕将∠PQR分成两个相等的角.
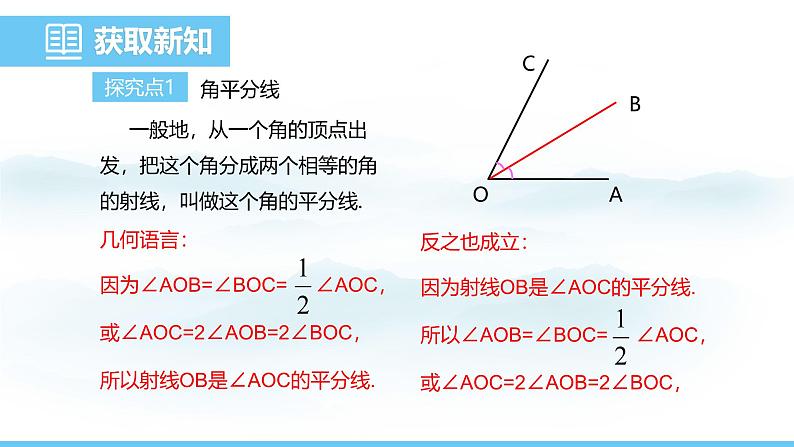
一般地，从一个角的顶点出发，把这个角分成两个相等的角的射线，叫做这个角的平分线.
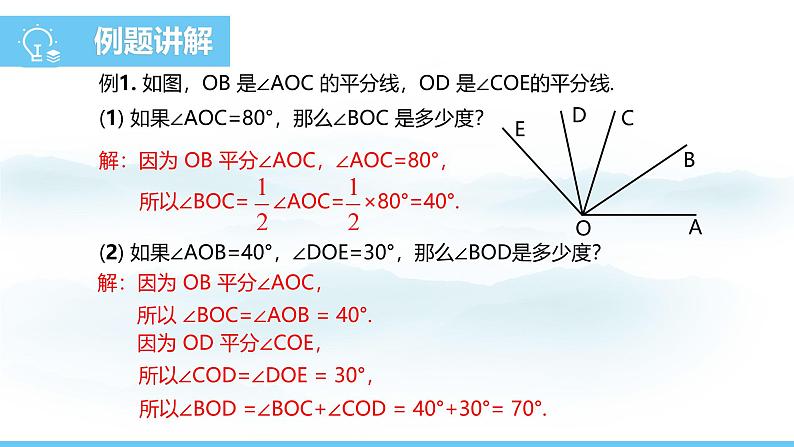
例1. 如图，OB 是∠AOC 的平分线，OD 是∠COE的平分线.(1) 如果∠AOC=80°，那么∠BOC 是多少度？
解：因为 OB 平分∠AOC，∠AOC=80°，
(2) 如果∠AOB=40°，∠DOE=30°，那么∠BOD是多少度？
解：因为 OB 平分∠AOC，
所以 ∠BOC=∠AOB = 40°.
因为 OD 平分∠COE，
所以∠COD=∠DOE = 30°，
所以∠BOD =∠BOC+∠COD = 40°+30°= 70°.
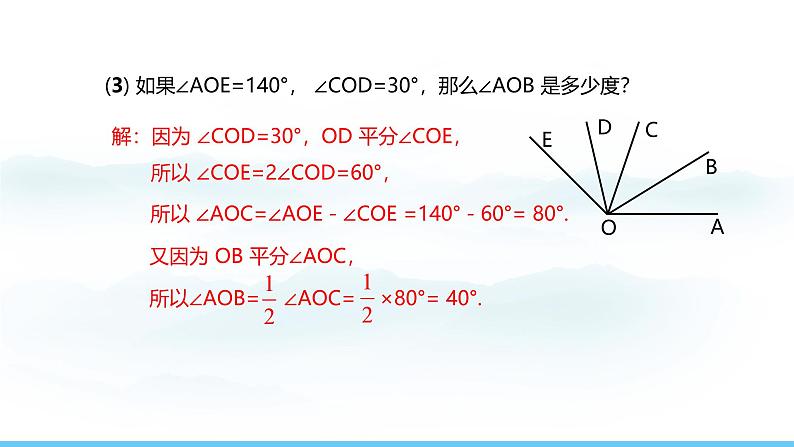
(3) 如果∠AOE=140°， ∠COD=30°，那么∠AOB 是多少度？
解：因为 ∠COD=30°，OD 平分∠COE，
所以 ∠COE=2∠COD=60°，
所以 ∠AOC=∠AOE－∠COE =140°－60°= 80°.
又因为 OB 平分∠AOC，
如图，O 是直线AB上一点，OC是∠AOB 的平分线，∠COD=31°28'.求∠AOD 的度数.
解：因为O 是直线AB上一点， 所以∠AOB=180°. 因为OC是∠AOB 的平分线，
因为∠COD=31°28'，所以∠AOD=90°-31°28'=58°32'.
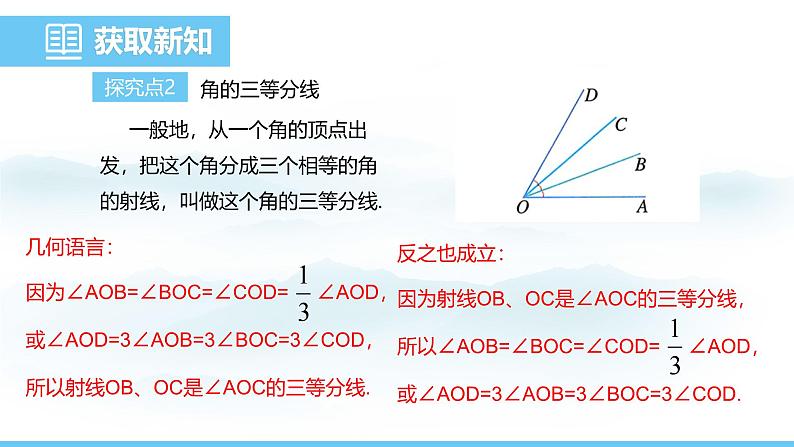
一般地，从一个角的顶点出发，把这个角分成三个相等的角的射线，叫做这个角的三等分线.
利用角的平分线的定义、角的和差倍分关系可以进行角度计算.
例2.把一个周角7等分，每份是多少度的角(精确到分)?解：360°÷7=51°+3°÷7=51°+180'÷7≈51°26’.答：每份是约51°26'的角.
说明：度、分、秒是六十进制的，不能整除时要把剩余的度数化成分
1.如图，把一个蛋糕等分成8份，每份中的角是多少度?要使每份中的角是15°，这个蛋糕应等分成多少份?
解：360°÷8=45°. 360°÷15°=24.答：把一个蛋糕等分成8份，每份中的角是45度； 要使每份中的角是15°，这个蛋糕应等分成24份.
2.计算：(1) 21°17'×5；(2)180°÷11(精确到分).
解：(1) 21°17'×5=105°85′=106°25′. (2)180°÷11=16°+4°÷11=16°+240′÷11≈16°+22′=16°22′.
分来讨论思想和方程思想在角度计算中的应用
例3.如图，已知∠AOB=40°，自O点引射线OC，若∠AOC：∠COB=2：3．求OC与∠AOB的平分线所成的角的度数．
解：分以下两种情况：
设∠AOC=2x，∠COB=3x，因为∠AOB=40°，所以2x+3x=40°，得x=8°，所以∠AOC=2x=2×8°=16°.因为OD平分∠AOB，所以∠AOD=20°，所以∠COD=∠AOD-∠AOC=20°-16°=4°．
如图，OC在∠AOB内部，OD平分∠AOB，
设∠AOC=2x，∠COB=3x，因为∠AOB=40°，所以3x-2x=40°，得x=40°，所以∠AOC=2x=2×40°=80°，因为OD平分∠AOB，所以∠AOD=20°，所以∠COD=∠AOC+∠AOD=80°+20°=100°．
如图，OC在∠AOB外部，OD平分∠AOB，
所以OC与∠AOB的平分线所成的角的度数为4°或100°．
方法总结涉及到角度的计算时，除常规的和差倍分计算外，通常还需运用方程思想和分类讨论思想解决问题.
1.如图，已知点O在直线MN上，OA平分∠PON，OB平分∠POM，则∠AOB的度数为（　　）​A．90° B．60° C．45° D．无法确定
2.如图，OE平分∠AOC，OD平分∠BOC，∠AOB=80°，∠1=15°，∠2=（　　）A.25° B．30° C．40° D．50°
3.如图，O为直线AB上一点，OC平分∠AOE，∠DOE=90°，有下列四个结论：①∠AOD+∠BOE=90°；②若∠BOE=58°，则∠COE=61°；③∠BOE=2∠COD；④OD平分∠COA．其中正确的是（　　）​A．①②③④ B．①②③ C．①②④ D．②③④
4. 已知∠AOB=38°，∠BOC=25°，那么∠AOC 的度数是 .
5.如图，点O在直线AB上．（1）若∠BOC：∠AOC=1：3，求∠BOC的度数；（2）若OD平分∠BOC，∠DOE=90°，OE平分∠AOC吗？为什么？
(2)平分．理由如下：因为OD平分∠BOC，所以∠BOD=∠DOC．因为∠DOC+∠COE=90°，所以∠AOE+∠BOD=90°．所以∠AOE=∠COE．所以OE平分∠AOC．
解：(1)因为∠BOC+∠AOC=180°， ∠BOC：∠AOC=1：3， 所以∠BOC+3∠BOC=180°， 所以∠BOC=45°．