

人教版(2024)七年级上册(2024)6.2 直线、射线、线段多媒体教学ppt课件
展开1. 会用尺规画一条线段等于已知线段,会比较两条线段的长短. (重点)2. 理解线段等分点的意义.3. 能够运用线段的和、差、倍、分关系求线段的长度. (重点、难点)4. 体会文字语言、符号语言和图形语言的相互转化.5. 了解两点间距离的意义,理解“两点之间,线段最短”的线段性质,并学会运用. (难点)
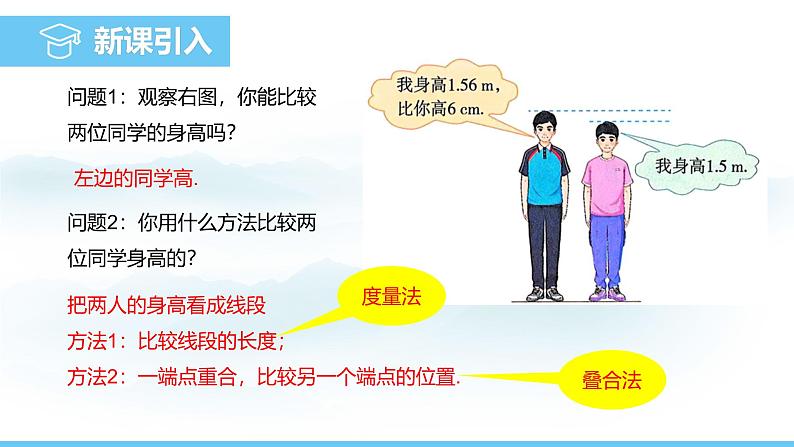
问题1:观察右图,你能比较两位同学的身高吗?
问题2:你用什么方法比较两位同学身高的?
把两人的身高看成线段方法1:比较线段的长度;方法2:一端点重合,比较另一个端点的位置.
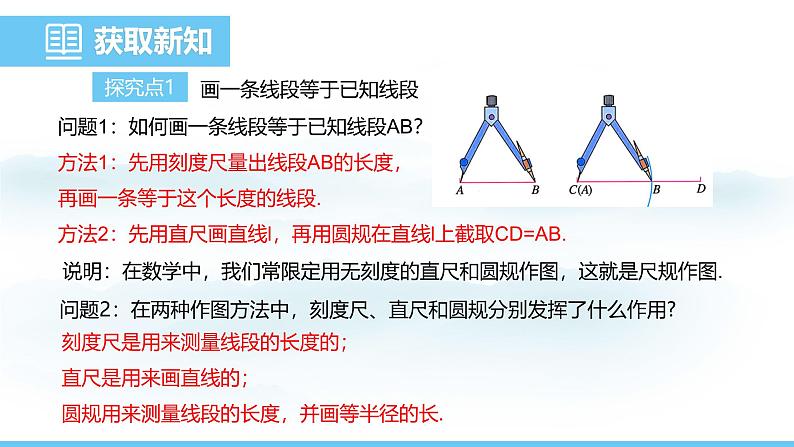
画一条线段等于已知线段
问题1:如何画一条线段等于已知线段AB?方法1:先用刻度尺量出线段AB的长度,再画一条等于这个长度的线段.方法2:先用直尺画直线l,再用圆规在直线l上截取CD=AB.
说明:在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
问题2:在两种作图方法中,刻度尺、直尺和圆规分别发挥了什么作用?
刻度尺是用来测量线段的长度的;直尺是用来画直线的;圆规用来测量线段的长度,并画等半径的长.
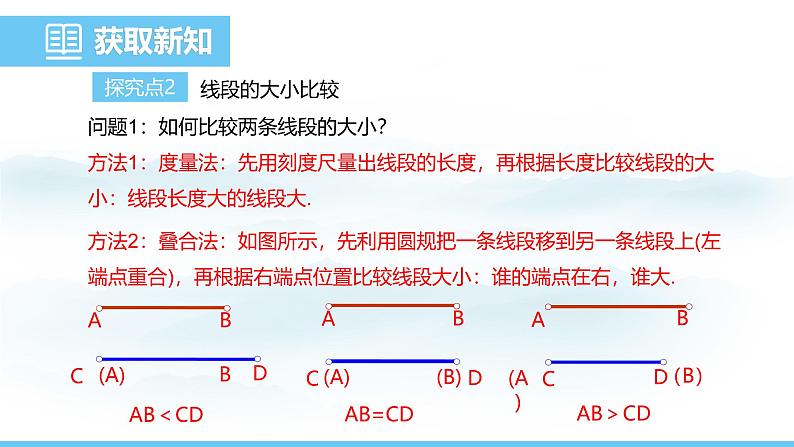
问题1:如何比较两条线段的大小?方法1:度量法:先用刻度尺量出线段的长度,再根据长度比较线段的大小:线段长度大的线段大.
方法2:叠合法:如图所示,先利用圆规把一条线段移到另一条线段上(左端点重合),再根据右端点位置比较线段大小:谁的端点在右,谁大.
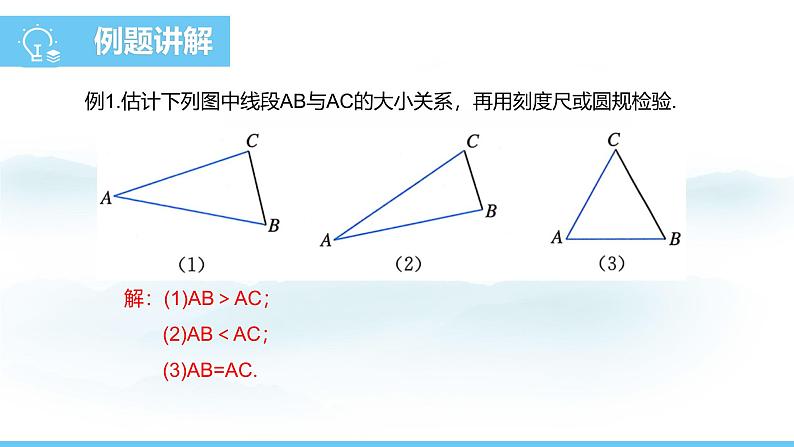
例1.估计下列图中线段AB与AC的大小关系,再用刻度尺或圆规检验.
解:(1)AB>AC; (2)AB<AC; (3)AB=AC.
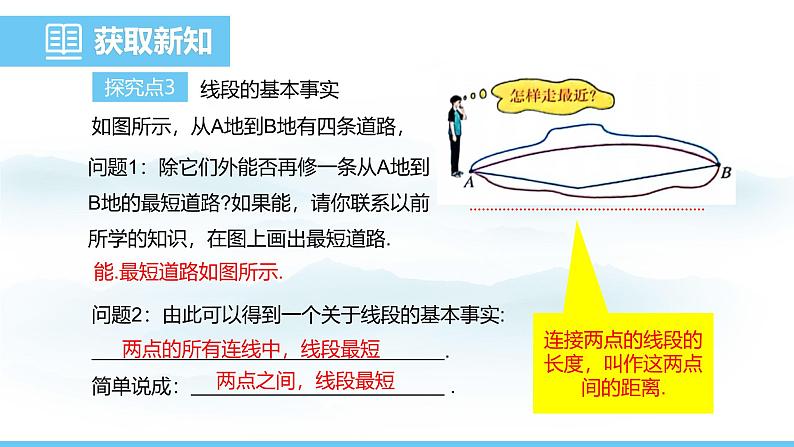
问题1:除它们外能否再修一条从A地到B地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短道路.
能.最短道路如图所示.
如图所示,从A地到B地有四条道路,
问题2:由此可以得到一个关于线段的基本事实: .简单说成: .
两点的所有连线中,线段最短
连接两点的线段的长度,叫作这两点间的距离.
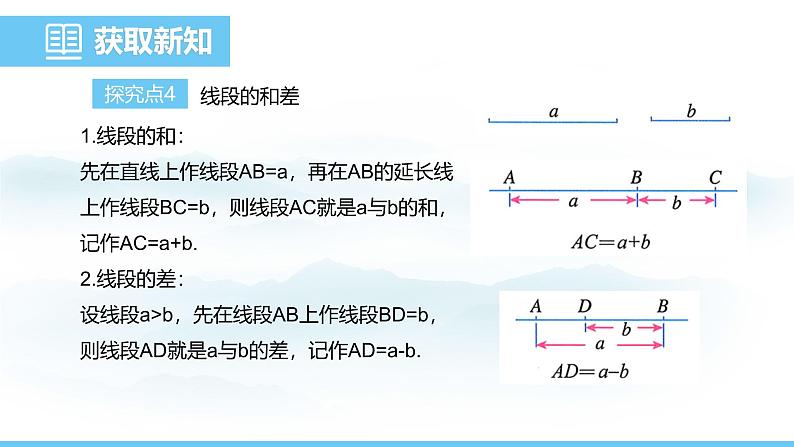
1.线段的和:先在直线上作线段AB=a,再在AB的延长线上作线段BC=b,则线段AC就是a与b的和,记作AC=a+b.2.线段的差:设线段a>b,先在线段AB上作线段BD=b,则线段AD就是a与b的差,记作AD=a-b.
例2.如图所示,已知线段a,b,作一条线段,使它等于 2a-b.
解:如图所示,在直线上作线段AB=a,再在线段AB的延长线上作线段BC=a,则线段AC=2a.在线段AC上作线段CD=b,则线段AD=2a-b.
如图,已知线段a,b,作一条线段,使它等于a+2b.
解:如图所示,在直线上作线段AB=a,再在线段AB的延长线上作线段BC=CD=b,则线段AD=a+2b.
1.线段的中点:如图,点M把线段AB分成相等的两条线段AM与MB,点M叫作线段AB的中点.
2.线段的三等分点:如图,点M、N把线段AB分成相等的三条线段AM、MN与NB,点M、N叫作线段AB的三等分点.
3.线段的四等分点:如图,点M、N、P把线段AB分成相等的四条线段AM、MN、NP与PB,点M、N、P叫作线段AB的四等分点.
例3.点M,N,P在同一条直线上,MN=3cm,NP=1cm.求线段MP的长.
解:如图所示,若点P在线段MN的延长线上, 则MP=MN+NP=3+1=4(cm).
如图所示,若点P在线段MN的延长线上,则MP=MN-NP=3-1=2(cm).
综上所述,MP的长为4cm或2cm.
1.在下列现象中,可以用基本事实“两点之间线段最短”来解释的是( )A.木工弹线 B.泥工砌墙 C.弯路改直 D.射击瞄准
2.如图,延长线段AB到点C,使BC=2AB,D是AC的中点,若AB=5,则BD的长为( )A.2 B.2.5 C.3 D.3.5
3.如图AB=CD,则AC与BD的大小关系是( )A.AC>BD B.AC<BD C.AC=BD D.无法确定
4.如图,点A,B在直线l上,点C,D在直线l外,则AC+CD+DB>AB,其依据是 .
5.如图,C、D两点在线段AB上,AC:CD:BD=1:2:4,点M为线段BC的中点,点N为线段CD的中点,且MN=4,则AB= .
6.如图是某同学在体育课上投掷四次铅球的成绩示意图,该同学投掷铅球最好成绩的点为 (填C,D,E,F中的一个字母).
AC是DB的2倍,AB是CD 的4倍.
8.如图,已知线段a,b,c,用尺规作线段AB=a+b-c.(不写作法,保留作图痕迹).解:如图,AB即为所求.
9.已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6,求CM和AD的长.
AD=10x=20 .
解:设AB=2x,BC=5x,CD=3x,
所以AD=AB+BC+CD=10x.
所以AM=MD=5x,
所以BM=AM-AB=3x.
即3x=6,所以x=2.
故CM=MD-CD=2x=4,
初中数学人教版(2024)七年级上册(2024)第六章 几何图形初步6.2 直线、射线、线段教学课件ppt: 这是一份初中数学人教版(2024)七年级上册(2024)<a href="/sx/tb_c4050891_t3/?tag_id=26" target="_blank">第六章 几何图形初步6.2 直线、射线、线段教学课件ppt</a>,共38页。PPT课件主要包含了学习目标,知识回顾,两点确定一条直线,新知导入,探究新知,归纳总结,56m,度量法,叠合法,叠合法结论等内容,欢迎下载使用。
初中数学人教版(2024)七年级上册(2024)第六章 几何图形初步6.2 直线、射线、线段教案配套ppt课件: 这是一份初中数学人教版(2024)七年级上册(2024)<a href="/sx/tb_c4050891_t3/?tag_id=26" target="_blank">第六章 几何图形初步6.2 直线、射线、线段教案配套ppt课件</a>,文件包含第1课时线段的比较pptx、两点之间线段最短mp4、尺规作图作一条线段等于已知线段mp4等3份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
初中数学人教版(2024)七年级上册6.2 直线、射线、线段课文ppt课件: 这是一份初中数学人教版(2024)七年级上册<a href="/sx/tb_c4050891_t3/?tag_id=26" target="_blank">6.2 直线、射线、线段课文ppt课件</a>,文件包含第1课时线段的比较pptx、两点之间线段最短mp4、尺规作图作一条线段等于已知线段mp4等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。













