数学七年级上册（2024）6.3 角教学ppt课件

这是一份数学七年级上册（2024）6.3 角教学ppt课件，共18页。PPT课件主要包含了学习目标，新课引入，互余的概念，探究点1，获取新知，互补的概念，探究点2，跟踪训练，互余的性质，探究点3等内容，欢迎下载使用。

1. 了解余角、补角的概念.(重点)2.掌握余角和补角的性质，并能利用余角、补角的知识解决相关问题.(重点、难点)
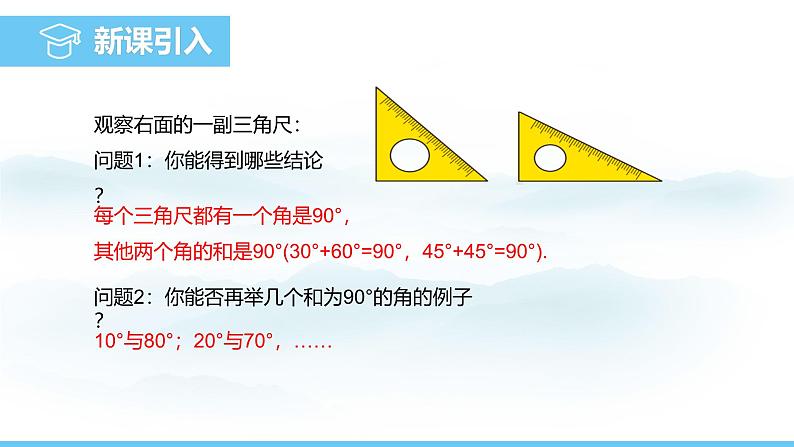
每个三角尺都有一个角是90°，其他两个角的和是90°(30°+60°=90°，45°+45°=90°).
观察右面的一副三角尺：问题1：你能得到哪些结论？
问题2：你能否再举几个和为90°的角的例子？
10°与80°；20°与70°，……
1.互余：如图所示，一般地，如果两个角的和等于90°(直角)，就说这两个角互为余角，简称这两个角互余，其中一个角是另一个角的余角.
反之也成立：因为∠1与∠2互为余角，或∠1是∠2的余角，或∠2是∠1的余角，所以∠1+∠2=90°.
2.几何语言：因为∠1+∠2=90°，所以∠1与∠2互为余角，或∠1是∠2的余角，或∠2是∠1的余角.
1.互补：如图所示，一般地，如果两个角的和等于180°(直角)，就说这两个角互为补角，简称这两个角互补，其中一个角是另一个角的补角.
反之也成立：因为∠1与∠2互为补角，或∠1是∠2的补角，或∠2是∠1的补角，所以∠1+∠2=180°.
2.几何语言：因为∠1+∠2=180°，所以∠1与∠2互为补角，或∠1是∠2的补角，或∠2是∠1的补角.
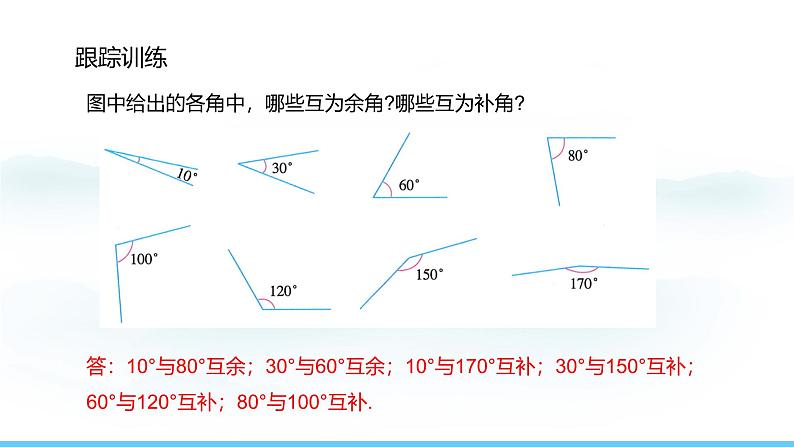
图中给出的各角中，哪些互为余角?哪些互为补角?
答：10°与80°互余；30°与60°互余；10°与170°互补；30°与150°互补；60°与120°互补；80°与100°互补.
2.一个角是70°39'，求它的余角和补角.解：余角为90°-70°39'=19°21'； 补角为180°-70°39'=109°21'.3.∠α的补角是它的3倍，∠α是多少度?解：因为∠α的补角是它的3倍， 所以∠α的补角是3∠α， 所以∠α+3∠α=180°， 所以∠α=45°.
问题1：∠1与∠2，∠3都互为余角，∠2与∠3的大小有什么关系?∠2=∠3.问题2：∠1与∠2，∠3与∠4都互为余角，且∠1=∠3，∠2与∠4的大小有什么关系?∠2=∠4.问题3：由此可以得到余角的什么性质?同角(等角)的余角相等.
问题4：如何用几何语言描述这两条性质？（1）因为∠1+∠2=90°，∠1+∠3=90°， 所以∠2=∠3.（2）因为∠1+∠2=90°，∠1+∠3=90°，且∠1=∠3， 所以∠2=∠4.
问题1：∠1与∠2，∠3都互为补角，∠2与∠3的大小有什么关系?∠2=∠3.问题2：∠1与∠2，∠3与∠4都互为补角，且∠1=∠3，∠2与∠4的大小有什么关系?∠2=∠4.问题3：由此可以得到补角的什么性质?同角(等角)的补角相等.
问题4：如何用几何语言描述这两条性质？（1）因为∠1+∠2=180°，∠1+∠3=180°， 所以∠2=∠3.（2）因为∠1+∠2=180°，∠1+∠3=180°，且∠1=∠3， 所以∠2=∠4.
例1.如图所示，点A，O，B在同一条直线上，射线OD 和射线OE分别平分∠AOC 和∠BOC.图中哪些角互为余角?解：因为点A，O，B在同一条直线上， 所以∠AOC和∠BOC 互为补角. 又因为射线 OD 和射线OE 分别平分∠AOC 和∠BOC， 所以∠COD 和∠COE 互为余角. 同理∠AOD 和∠BOE，∠AOD 和∠COE，∠COD 和∠BOE 也互为余角.
2.如图，要测量两堵围墙所形成的∠AOB 的度数，但人不能进入围墙，如何测量?
解：延长 AO 到点D，延长 BO到点C，方法1：测量∠COD的度数，根据同角的补角相等，可得∠AOB=∠COD；方法2：测量∠AOC的度数，根据补角的概念，可得∠AOB=180°-∠AOC；方法3：测量∠BOD的度数，根据补角的概念，可得∠AOB=180°-∠BOD.
例2.如图，已知O为AD上一点，∠AOC与∠AOB互补，OM，ON分别为∠AOC，∠AOB的平分线，若∠MON=40°，试求∠AOC与∠AOB的度数．
解：设∠AOB=x，因为∠AOC与∠AOB互补，则∠AOC=180°-x．因为OM，ON分别为∠AOC，∠AOB的平分线，
解得x=50°，则180°-x=130°.即∠AOB=50°，∠AOC=130°.
1.如图，点O在直线AE上，∠AOB=∠COD=90°，则图中除了直角外，一定相等的角有（　　）A．1对B．2对C．3对D．4对
2.一个角的度数是50°，那么它的余角的补角的度数是（　　）A．130°B．140°C．50°D．90°
3.如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，则∠A的余角是 和 ，∠ACD= ，理由是 ．
4.已知∠a和∠β互余，且∠a比∠β大20°，那么∠a的补角度数为 ．
5.如图，平面内∠AOB=∠COD=90°，∠AOE=∠DOE，点E，O，F在一条直线上，下列结论：①∠AOC=∠BOD；②∠AOD与∠BOC互补；③OF平分∠BOC；④∠AOD-∠BOF=90°．其中正确结论的有 （把所有正确结论的序号都选上）
6.如图，已知点O为直线AB上一点，∠BOC=110°，∠COD=90°，OM平分∠AOC．(1)求∠MOD的度数；(2)若∠BOP与∠AOM互余，求∠COP的度数．
解：（1）∵∠BOC=110°，∠COD=90°，∴∠BOC+∠COD=110°+90°=200°，∵∠AOB=180°，∴∠AOD=20°，∠AOC=180°-110°=70°，∵OM平分∠AOC，∴∠MOD=∠AOM+∠AOD=35°+20°=55°；
（2）∵∠BOP与∠AOM互余，∴∠BOP+∠AOM=90°，∵∠AOB=180°，∴∠MOP=180°-90°=90°，∵OM平分∠AOC，∴∠COP=∠MOP-∠COM=90°-35°=55°．