





数学鲁教版(五四学制)(2024)2 图形的旋转优质课课件ppt
展开旋转的基本性质:◆对应点到旋转中心的距离 . ◆对应点与旋转中心所连线段的夹角等于 . ◆旋转前、后的图形 . ◆图形的旋转是由 和旋转的决定.
作图工具:尺、规、笔. 基本作图技能: 作一条直线平行于已知直线; 作一线段等于已知线段; 作一角等于已知角.
回顾已经学过的尺规作图
旋转中心,用点表示;旋转方向分为顺时针方向和逆时针方向. 角度,用量角器度量,或通过画角度等于已知角.
简单旋转作图的一般步骤:(1)找出图形的关键点;(2)确定旋转中心、旋转方向和旋转角;(3)将关键点与旋转中心连接起来,然后按旋转方向 分别将它们旋转一个角度,得到关键点的对应点;(4)按照原图形的顺序连接这些对应点,所得到的图 形就是旋转后的图形.
确定旋转中心的方法:要看旋转中心是在图形上还是不在图形上.若在图形上,哪一点在旋转的过程中位置没有改变,这一点就是旋转中心;若不在图形上,任意两对对应点连线的垂直平分线的交点就是旋转中心.
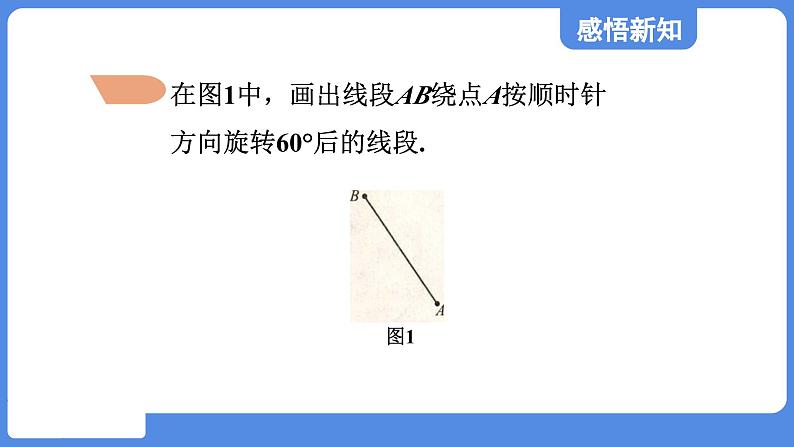
在图1中,画出线段AB绕点A按顺时针方向旋转60°后的线段.
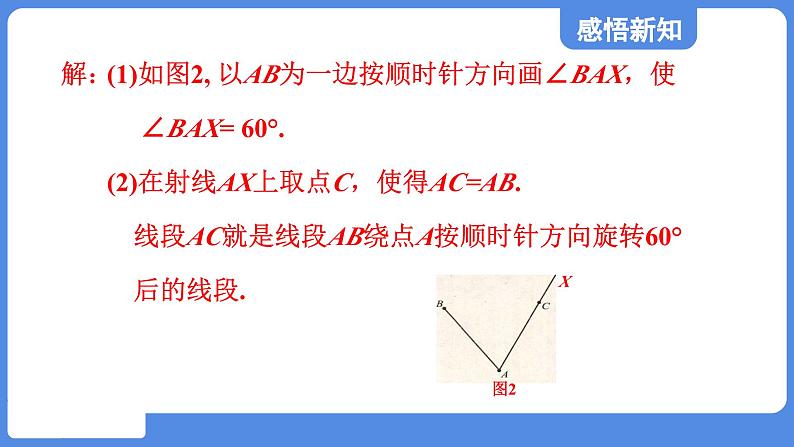
(1)如图2, 以AB为一边按顺时针方向画∠BAX,使 ∠BAX= 60°. (2)在射线AX上取点C,使得AC=AB. 线段AC就是线段AB绕点A按顺时针方向旋转60° 后的线段.
如图,△ABC绕点O旋转,使点A旋转到点D处,画出顺时针旋转后的三角形,并写出简要作法.
抓住“关键点”A,B,C,D,旋转中心O,旋转角∠AOD这些要素,按步骤“连——转——截——连”即可得出所求作的三角形.作法:(1)连接OA,OB,OC,OD;(2)分别以OB,OC为边作∠BOM=∠CON=∠AOD;(3)分别在OM,ON上截取OE=OB,OF=OC;(4)依次连接DE,EF,FD; 则△DEF就是所求作的 三角形,如图所示.
在旋转作图时,要紧扣以下三点:(1)对应点到旋转中心的距离相等;(2)旋转的角度相等;(3)旋转的方向相同.
1. 为了避免作图混乱,也可以先对一个关键点连、转、截,找到其对应点后再进行下一个关键点的旋转;2. 已知旋转中心和一对对应点,画旋转图形时要先将这对对应点与旋转中心相连, 找出旋转方向和旋转角. 由此将此类问题转化成已知旋转三要素的旋转作图.
如图,在方格纸上,△DEF是由△ABC绕定点P顺时针旋转得到的,如果用(2,1)表示方格纸上A点的位置, (1,2)表示B点的位置,那么点P的位置为( )A.(5,2) B.(2,5) C.(2,1) D.(1,2)
如图,分别连接AD,CF,然后作它们的垂直平分线,相交于P点,则旋转中心为P,易得点P的坐标为(5,2).
确定旋转中心与旋转角的方法: 在图形的旋转过程中,判断谁是旋转中心,要看旋转中心是在图形上还是不在图形上;若在图形上,哪一点在旋转过程中位置没有改变,这一点就是旋转中心;若不在图形上,对应点连线的垂直平分线的交点就是旋转中心,旋转角等于对应点与旋转中心所连线段的夹角.
在图中画出线段AB绕点O按顺时针方向旋转50°后的线段.
如图,过O在AB右侧作∠AOF=50°,在OF上截取OC=OA,延长FO,在FO的延长线上截取OD=OB,线段CD就是线段AB绕点O按顺时针方向旋转50°后的线段.
将如图所示的五边形绕点O按顺时针方向旋转 90°,画出旋转后的图形.
过点O分别作各个顶点与点O连线的垂线,并在每条垂线上截取与相应线段相等的线段,得到各个顶点绕O点按顺时针方向旋转90°后的对应点,然后按原来的方式连接相应的顶点即可得到旋转后的图形(如图).
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么点A(-2,5)的对应点 A′的坐标是________.
问 题让我们一起来欣赏一下美丽的图案,体会一下旋转的奥秘.你们猜猜旋转到底和什么有关呢?
(1)旋转中心不变,改变旋转角(如图).
(2)旋转角不变,改变旋转中心.
(3)美丽的图案是这样形成的.
我们可以利用旋转中心不变,改变旋转角;旋转角不变,改变旋转中心设计许多美丽的图案.
如图(1)是某一种花的花瓣和中心,现以 O 为旋转中 心画出分别旋转 45°, 90° ,135° ,180° , 225°, 270°, 315°的这种花的图形.解:如图(2).
本题是将基本图形按旋转图形的作法,分别按七个角度作旋转图形.作旋转图形时注意旋转三要素:旋转中心、旋转方向、旋转角.
同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的.如图是在万花筒中看到的一个图案.图中所有小三角形均是全等的等边三角形,其中的四边形AEFG可以看成是四边形ABCD以A为旋转中心( )A.顺时针旋转60°得到的B.顺时针旋转120°得到的C.逆时针旋转60°得到的D.逆时针旋转120°得到的
导引:根据图形可知∠BAE=120°,AB边绕点A顺时针旋转120°得到AE边,所以菱形AEFG可以看成是把菱形ABCD以A为旋转中心顺时针旋转120° 得到的.
如图是甲、乙两张不同的纸片,将它们 分别沿着 虚线剪开后,各自要拼一个与原来面积相等的正方形, 则( ) A.甲、乙都可以 B.甲、乙都不可以 C.甲不可以,乙可以 D.甲可以,乙不可以
练点 旋转画图
1. 如图,在方格纸中,将Rt△ AOB 绕点 B 按顺时针方向旋 转90°后得到Rt△ A ' O ' B ,则下列四个图形中正确的是 ( B )
A B C D
2. [2024·济南月考]如图,在平面直角坐标系中,△ ABC 绕 旋转中心顺时针旋转90°后得到△ A ' B ' C ',则其旋转中 心的坐标是 .
作线段 BB '与线段 AA '的垂直平分线,其交点即为旋转中心.
3. [情境题·游戏活动型]在俄罗斯方块游戏中,有一个图案正 在下落,为了使这个图案可以和下面的图案全部消失,则 可以进行的操作是 .
绕点 O 顺时针旋转90°,再向右平移
至最右侧(答案不唯一)
旋转作图的一般步骤:一连:连接已知点与旋转中心;二定:确定旋转方向;三量:测量旋转角度;四截:在旋转角的另一条边上以旋转中心为一端点截取等于对应线段长度的线段;五画:顺次连接所得的点,从而画出旋转得到的图形.
初中数学鲁教版(五四学制)(2024)八年级上册2 图形的旋转一等奖ppt课件: 这是一份初中数学鲁教版(五四学制)(2024)八年级上册<a href="/sx/tb_c100391_t3/?tag_id=26" target="_blank">2 图形的旋转一等奖ppt课件</a>,共43页。PPT课件主要包含了观察下面现象,回顾与思考,知识点,旋转及相关概念,∠BED,旋转的性质,或120等内容,欢迎下载使用。
九年级上册3.2 图形的旋转一等奖课件ppt: 这是一份九年级上册3.2 图形的旋转一等奖课件ppt,共25页。PPT课件主要包含了学习目标,回顾平移的特征,复习回顾,简单的旋转作图,知识精讲,针对练习,平移和旋转的异同,典例解析,∠ADE,旋转作图的基本步骤等内容,欢迎下载使用。
中考数学复习专项训练一网格作图题类型二旋转在网格中的作图作业课件: 这是一份中考数学复习专项训练一网格作图题类型二旋转在网格中的作图作业课件,共10页。PPT课件主要包含了轴对称等内容,欢迎下载使用。













