初中数学北师大版（2024）七年级上册（2024）1 认识有理数备课ppt课件

这是一份初中数学北师大版（2024）七年级上册（2024）1 认识有理数备课ppt课件，共23页。PPT课件主要包含了第1课时有理数，2认识有理数，零上5ºC，零下5ºC，不回答，有理数按定义，负分数，正分数，负整数，正整数等内容，欢迎下载使用。

世界上最高的山峰是珠穆朗玛峰，其海拔大约是8848.86 m,吐鲁番盆地最低处的海拔大约是-154.31 m。你能说出-154.31m的含义吗?怎样计算珠穆朗玛峰的海拔和吐鲁番盆地最低处的海拔相差多少呢?
本章将在小学学习的基础上引入负数，将数的范围扩充到有理数。你将经历从具体情境中抽象出负数的过程，理解有理数运算的意义并进行正确运算，通过归纳、类比、转化等发现一些数学结论，提高运算能力和推理能力，发展应用意识等。
1.在具体情境中，进一步认识负数，理解有理数的意义(重点)；2. 经历用正负数表示具有相反意义的量的过程，体会负数是实际生活的需要(重点)；3.会判断一个数是正数还是负数，能按一定的标准对有理数进行分类(难点)。
1.小学我们学过的数包括哪些？
自然数、整数、分数、小数。
2.数学中仅有这些数够用了吗？用小学学过的数能表示下列数吗？
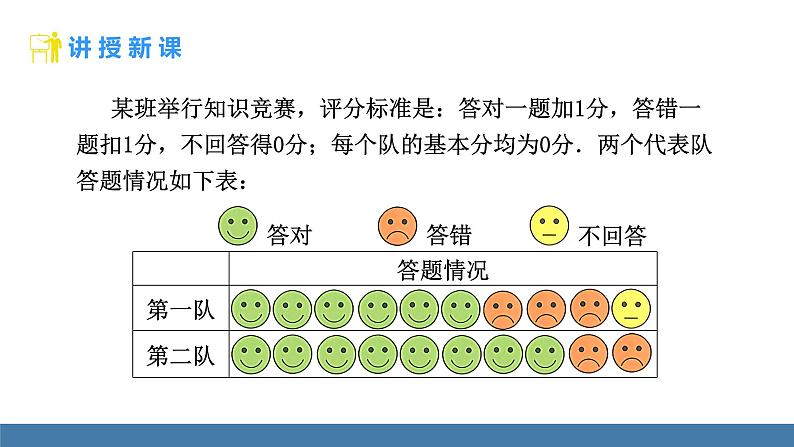
某班举行知识竞赛，评分标准是：答对一题加1分，答错一题扣1分，不回答得0分；每个队的基本分均为0分．两个代表队答题情况如下表：
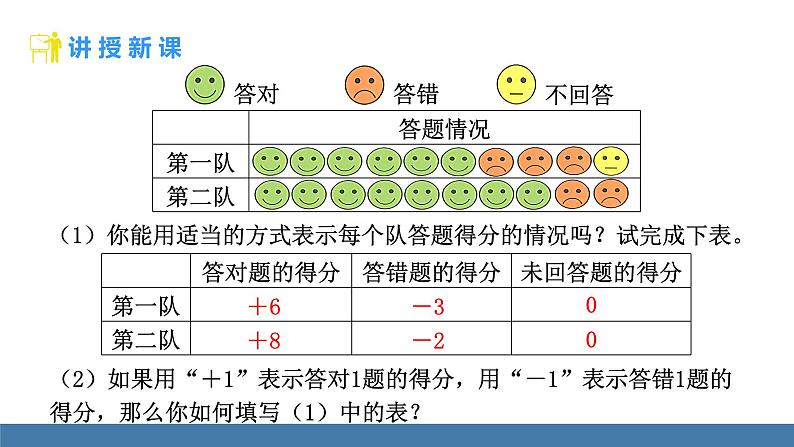
（1）你能用适当的方式表示每个队答题得分的情况吗？试完成下表。
（2）如果用“＋1”表示答对1题的得分，用“－1”表示答错1题的得分，那么你如何填写（1）中的表？
（1）下表是2023年1月1日四个城市的气温情况。你能说出表中各数的实际意义吗？
（2）珠穆朗玛峰的海拔大约是8 848.86m，吐鲁番盆地最低处的海拔大约是－154.31m。8 848.86m，－154.31m两数的实际意义分别是什么？
－7℃指零下7摄氏度，5℃指零上5摄氏度。
8 848.86m指高于海平面8848.86m；－154.31m指低于海平面154.31m。
（3）下图展示了2021年7月我国居民消费价格分别同比涨跌情况。说说－1.8%，0.4%等数的实际意义，并与同伴进行交流。
－1.8%指下跌量为1.8%，0.4%指上涨量为0.4%。
为了表示具有相反意义的量，我们可以把其中一个量规定为正的，把与这个量意义相反的量规定为负的，并分别“＋”“－”来表示。 例如，“加3分”记为＋3分，“扣2分”就记为－2分。
像＋3,＋15,＋6.9%,…都是正数，正数前面的“＋”可以省略不写。 像－2,－8,－1.8%,…都是负数。 0既不是正数，也不是负数。
负数与对应的正数在数量上相等，表示的意义相反。
☀归纳 判断正数、负数的方法：首先要确定它不为0；其次看它的“＋”“－”号的呈现形式：若不含“＋”“－”号，或只含“＋”号，则均为正数，否则为负数.
例2 (1)某人转动转盘，如果用＋5圈表示沿逆时针方向转了5圈，那么沿顺时针方向转了12圈怎样表示?(2)在某次乒乓球质量检测中，一只乒乓球的质量高于标准质量0.02g，记作＋0.02 g,那么－0.03 g表示什么?(3)某大米包装袋上标注着“净含量：10 kg±50 g”,这里的“10 kg±50 g”表示什么?
解:(1)沿顺时针方向转了12圈记作－12圈；(2)－0.03g表示乒乓球的质量低于标准质量0.03g;(3)每袋大米的标准质量应为10kg,但实际每袋大米可能有50g的误差,即每袋大米的净含量最多是10kg＋50g,最少是10kg－50g。
用正数和负数表示具有相反意义的量的“三步法”：(1)确定问题中存在具有相反意义的量。(2)明确具有相反意义的量的“基准”，把一种意义的量规定为正，另一种和它意义相反的量则为负。(3)用符号、数和单位分别表示出问题中具有相反意义的量。
(1)选定一个身体高度作为标准，用正负数和0表示你们班每名同学的身高与选定的身高标准的差。你是怎样表示的?从你的表示能看出谁最高吗?
如把160cm作为本班同学的标准身高，超过160cm的部分用正数表示，如170cm，超过10cm表示为“＋10cm”，不足160cm的部分用负数表示，如158cm,差2cm表示为“－2cm”.
☀归纳 (1)0既不是正数，也不是负数。(2)0是整数与负数的分界线。(3)0不仅可以表示“没有”，还可以表示特定意义。
例3 (1)一个月内，李明体重增加1.2 kg，张华体重减少0.5 kg,刘伟体重无变化，写出他们这个月的体重增长值。(2)四种品牌的手机今年的销售量与去年相比，变化率如下：A品牌减少2%,B品牌增长4%,C品牌增长1%,D品牌减少3%写出今年这些品牌的手机销售量的增长率
解：(1)这个月李明体重增长1.2 kg,张华体重增长-0.5 kg,刘伟体重增长0 kg。(2)四种品牌的手机今年销售量的增长率是：A品牌 -2%,B品牌 4%,C品牌 1%，D品牌 -3%。
(2)你能将所学的数进行分类吗?与同伴进行交流。
如－1,－2,－3,…
整数和分数统称为有理数。
有理数还可以进行其他分类吗？
小学学过的小数是不是有理数？属于分类中的哪一类？有限小数和无限循环小数都是有理数，属于分数，是有理数；无限不循环小数不是有理数,比如π。
1．我国古代数学名著《九章算术》中对正负数的概念注有“今两算得失相反，要令正负以名之”。如果把收入5元记作＋5元，那么支出5元记作（    ）A．0元B．－5元 C．＋5元 D．＋10元2．在这四个数－1,0,1,2中，既不是正数，也不是负数的是（  ）A．－1B．0 C．1 D．23．若x是正数，则x 0。（填“＞”或“＜”或“＝”）4．如果温度上升3℃，记作＋3℃，那么温度下降2℃记作 ℃。