人教B版高中数学必修第一册第3章3-1-1第2课时函数的表示方法课件

这是一份人教B版高中数学必修第一册第3章3-1-1第2课时函数的表示方法课件，共52页。
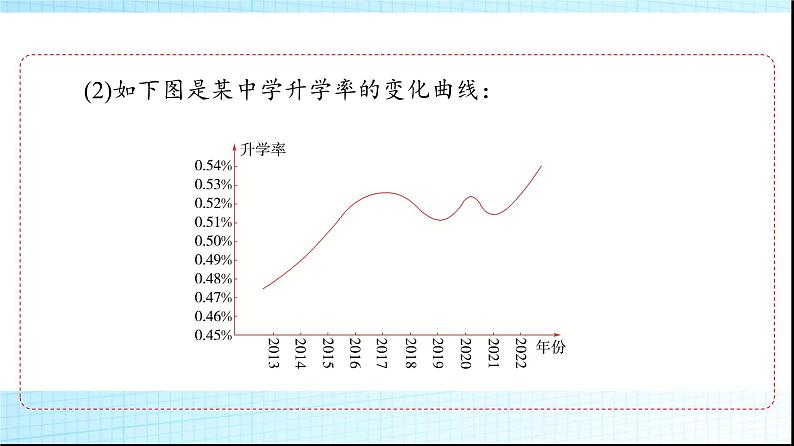
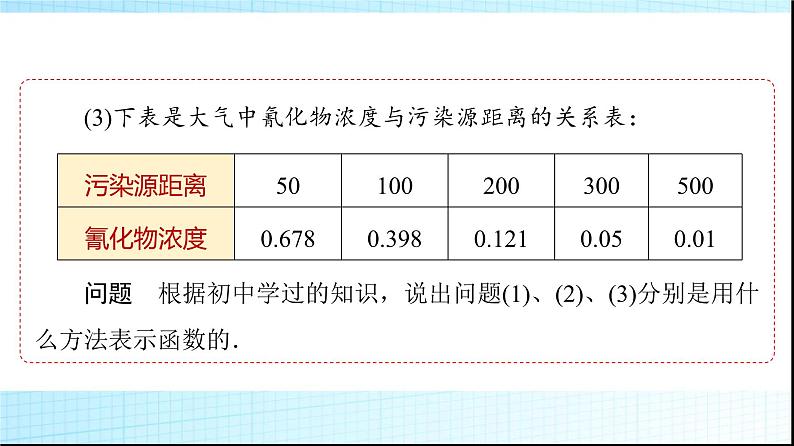
第2课时　函数的表示方法第三章　函数3.1　函数的概念与性质3.1.1　函数及其表示方法必备知识·情境导学探新知(1)已建成的京沪高速铁路总长约1 318千米，设计速度目标值为380千米/时．若京沪高速铁路时速按300千米/时计算，火车行驶x小时后，路程为y千米，则y是x的函数，可以用y＝300x来表示，其中y＝300x叫做该函数的解析式．(2)如下图是某中学升学率的变化曲线：(3)下表是大气中氰化物浓度与污染源距离的关系表：问题　根据初中学过的知识，说出问题(1)、(2)、(3)分别是用什么方法表示函数的．知识点1　函数的表示方法代数式(或解析式)图象表格提醒　对3种表示法的说明思考　1．任何一个函数都可以用解析法、列表法、图象法三种形式表示吗？ 知识点2　用集合语言对函数的图象进行描述(1)定义：将函数y＝f (x)，x∈A中的自变量x和对应的函数值y，分别看成平面直角坐标系中点的横坐标与纵坐标，则满足条件的点(x，y)组成的集合F称为函数的图象，即F＝{(x，y)|y＝f (x)，x∈A}．(2)F是函数y＝f (x)的图象，必须满足下列两条：①图象上________的坐标(x，y)都满足函数关系y＝f (x)；②满足函数关系y＝f (x)的点(x，y)都在______________．任意一点函数的图象F上知识点3　分段函数如果一个函数，在其定义域内，对于自变量的不同________，有不同的________，则称其为分段函数．[提示]　分段函数是一个函数，而不是几个函数．取值区间对应方式思考　2．分段函数是一个函数还是几个函数？提醒　分段函数的定义域、值域和图象(1)定义域：各段自变量取值范围的并集，注意各段自变量取值范围的交集为空集．(2)值域：各段函数在相应区间上函数取值集合的并集．(3)图象：根据不同定义域上的解析式分别作出，再将它们组合在一起得到整个分段函数的图象．23题号41  ×23题号41(2)函数y＝|x|不是分段函数． (　　) ×[提示]　常数函数的图象是垂直于y轴的直线．×(3)常数函数的图象是垂直于x轴的直线． (　　)23题号411　[由题设给出的表知f (3)＝4，则f ( f (3))＝f (4)＝1．]2．已知函数f (x)由下表给出，则f ( f (3))＝________．123题号41   23题号411　3　[由f (x)的表格可得f (2)＝2，则由函数图象可知g( f (2))＝g(2)＝1，由函数图象可知g(2)＝1，由表格可知f (1)＝3，故f (g(2))＝3．]4．已知函数y＝f (x)的对应关系如表所示，函数y＝g(x)的图象是如图所示的曲线ABC，其中A(1，3)，B(2，1)，C(3，2)，则g( f (2))的值为______，f (g(2))的值为________．13关键能力·合作探究释疑难类型1　函数的3种表示方法【例1】　某商场新进了10台彩电，每台售价3 000元，试求售出台数x与收款数y之间的函数关系，分别用列表法、图象法、解析法表示出来．[解]　①列表法如下：②图象法如图所示：③解析法：y＝3 000x，x∈{1，2，3，…，10}．反思领悟　1．函数的3种表示法的选择解析法、图象法和列表法分别从三个不同的角度刻画了自变量与函数值的对应关系．采用解析法的前提是变量间的对应关系明确，采用图象法的前提是函数的变化规律清晰，采用列表法的前提是定义域内自变量的个数较少．2．用3种方法表示函数时要注意的问题(1)解析法必须注明函数的定义域．(2)列表法必须罗列出所有的自变量与函数值的对应关系．(3)图象法必须清楚函数图象是“点”还是“线”．[跟进训练]1．如图，点P在边长为1的正方形的边上运动，M是CD的中点，则当P沿A-B-C-M运动时，点P经过的路程x与△APM的面积y的函数y＝f (x)的图象的形状大致是(　　)A　　　　　　　B 　　　　　C　　　　　　　D√ 类型2　函数解析式的求法考向1　待定系数法求函数解析式【例2】　(1)已知f (x)是一次函数，且满足2f (x＋3)－f (x－2)＝2x＋21，求f (x)的解析式．(2)已知f (x)为二次函数，且满足f (0)＝1，f (x－1)－f (x)＝4x，求f (x)的解析式．[解]　(1)设f (x)＝ax＋b(a≠0)，则2f (x＋3)－f (x－2)＝2[a(x＋3)＋b]－[a(x－2)＋b]＝2ax＋6a＋2b－ax＋2a－b＝ax＋8a＋b＝2x＋21，所以a＝2，b＝5，所以f (x)＝2x＋5．(2)因为f (x)为二次函数，设f (x)＝ax2＋bx＋c(a≠0)．由f (0)＝1，得c＝1．又因为f (x－1)－f (x)＝4x，所以a(x－1)2＋b(x－1)＋c－(ax2＋bx＋c)＝4x，整理，得－2ax＋a－b＝4x，求得a＝－2，b＝－2，所以f (x)＝－2x2－2x＋1．  x2－4x＋3(x≥1)       √  f (x)＝2x＋2或f (x)＝－2x－6   [解]　(1)f (－4)＝－4＋2＝－2，f (3)＝2×3＝6，f (－2)＝－2＋2＝0，f ( f (－2))＝f (0)＝02＝0．  反思领悟　分段函数问题的常见解法(1)求分段函数的函数值的方法：先确定要求值的自变量的取值属于哪一段区间，然后代入该段的解析式求值．当出现f (f (a))的形式时，应从内到外依次求值．(2)已知分段函数的函数值，求自变量的值的方法：先假设自变量的值在分段函数定义域的各段上，然后求出相应自变量的值，切记要检验．(3)在分段函数的前提下，求某条件下自变量的取值范围的方法：先假设自变量的值在分段函数定义域的各段上，然后求出在相应各段定义域上自变量的取值范围，再求它们的并集即可． √    反思领悟　描点法作函数图象的3个关注点(1)画函数图象时首先关注函数的定义域，即在定义域内作图．(2)图象是实线或实点，定义域外的部分有时可用虚线来衬托整个图象．(3)要标出某些关键点，例如图象的顶点、端点、与坐标轴的交点等．要分清这些关键点是实心点还是空心点．提醒：(1)函数图象既可以是连续的曲线，也可以是直线、折线、离散的点等．(2)分段函数的图象是在同一个直角坐标系内分别作出各段的图象，在作图时要特别注意接点处点的虚实，保证不重不漏．  学习效果·课堂评估夯基础23题号41  √23题号41√A　[令x＋1＝t，则x＝t－1，∴f (t)＝3(t－1)＋2＝3t－1．∴f (x)＝3x－1．]2．已知函数f (x＋1)＝3x＋2，则f (x)的解析式是(　　)A．f (x)＝3x－1 B．f (x)＝3x＋1C．f (x)＝3x＋2 D．f (x)＝3x＋423题号41   23题号41 4．函数y＝f (x)的图象如图所示，则其解析式为_______________________． [提示]　解析法、列表法、图象法．回顾本节知识，自主完成以下问题：1．函数的三种表示方法是什么？[提示]　(1)分段函数是一个函数，而不是几个函数．处理分段函数问题时，要先确定自变量的取值在哪个区间，从而选取相应的对应关系．(2)分段函数在书写时用大括号把各段函数合并写成一个函数的形式，并且必须指明各段函数自变量的取值范围．(3)分段函数的定义域是所有自变量取值区间的并集．分段函数的定义域只能写成一个集合的形式，不能分开写成几个集合的形式．(4)分段函数的值域是各段函数在对应自变量的取值范围内值域的并集．2．你是怎样理解分段函数的？[提示]　待定系数法、换元法、配凑法、消元法、解方程组等方法．3．求函数的解析式有哪些常用方法？