新教材人教B版步步高学习笔记【同步课件】第三章 章末复习课

这是一份新教材人教B版步步高学习笔记【同步课件】第三章 章末复习课，共41页。

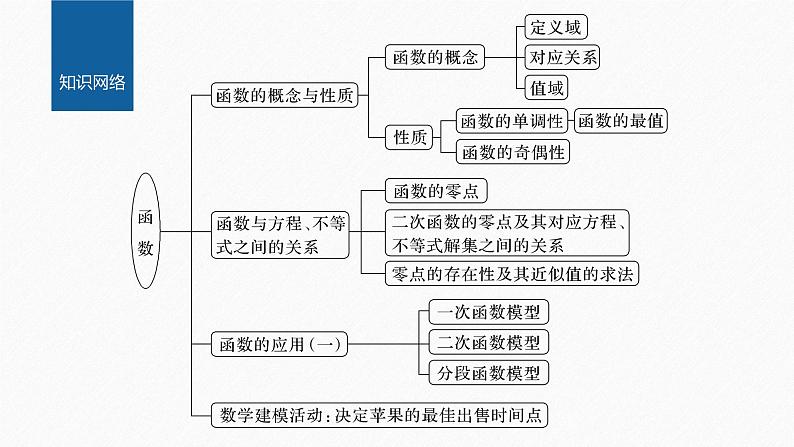
章末复习课第三章　函　数知识网络内容索引函数的定义域 一1.函数的定义域是指函数y＝f(x)中自变量x的取值范围.实际问题确定的函数的定义域要考虑让实际问题有意义.2.考查函数的定义域的问题，主要是考查逻辑思维能力、综合分析能力和计算能力.√(2)已知函数y＝f(x＋1)的定义域是[－2,3]，则y＝f(2x－1)的定义域是A. B.[－1,4]C.[－5,5] D.[－3,7]√设u＝x＋1，由－2≤x≤3，得－1≤x＋1≤4，所以y＝f(u)的定义域为[－1,4].求函数定义域的类型与方法(1)已给出函数解析式：函数的定义域是使解析式有意义的自变量的取值集合.(2)实际问题：求函数的定义域既要考虑使解析式有意义，还应考虑使实际问题有意义.(3)复合函数问题：①若f(x)的定义域为[a，b]，f(g(x))的定义域应由a≤g(x)≤b解出；②若f(g(x))的定义域为[a，b]，则f(x)的定义域为g(x)在[a，b]上的值域.反思感悟 (1)函数f(x)＝ 的定义域是A.[－1，＋∞) B.(－∞，－1]C.R D.[－1,1)∪(1，＋∞)√故定义域为[－1,1)∪(1，＋∞)，故选D.(2)设函数f(x)的定义域为[1,5]，则函数f(2x－3)的定义域为A.[2,4] B.[3,11]C.[3,7] D.[1,5]√由题意得，1≤2x－3≤5，解得2≤x≤4，所以函数f(2x－3)的定义域是[2,4].函数的解析式 二1.函数的解析式实际上就是函数的对应法则的数学表示，求函数的解析式一般采用的是换元法、拼凑法、待定系数法、解方程组法等，特别是在分段函数中还要结合函数的奇偶性.2.求函数的解析式往往考查的是分析能力和逻辑思维能力，以提高逻辑思维和数学运算的素养为主要目的. (1)函数f(x)在R上为奇函数，当x>0时，f(x)＝ ＋1，则f(x)的解析式为_______________________.设x<0，则－x>0，∵f(x)是奇函数，∴f(－x)＝－f(x)，∵f(x)是奇函数，∴f(0)＝0，f(x)＝x2－x＋1，x∈(－∞，1)∪___________.(1，＋∞)所以所求函数的解析式为f(x)＝x2－x＋1，x∈(－∞，1)∪(1，＋∞).求函数解析式的题型与相应的解法(1)已知形如f(g(x))的解析式求f(x)的解析式，使用换元法或配凑法.(2)已知函数的类型(往往是一次函数或二次函数)，使用待定系数法.(3)含f(x)与f(－x)或f(x)与  ，使用解方程组法.(4)已知一个区间的解析式，求另一个区间的解析式，可用奇偶性转移法.反思感悟 (1)已知二次函数f(x)满足f(0)＝1，f(1)＝2，f(2)＝5，则该二次函数的解析式为_____________.f(x)＝x2＋1设二次函数的解析式为f(x)＝ax2＋bx＋c(a≠0)，(2)若3f(x－1)＋2f(1－x)＝2x，则f(x)的解析式为____________.令t＝x－1，则x＝t＋1，t∈R，原式变为3f(t)＋2f(－t)＝2(t＋1). ①以－t代替t，①式变为3f(－t)＋2f(t)＝2(1－t). ②函数的单调性和奇偶性 三1.函数的单调性和奇偶性是函数的两种非常重要的性质，既能作为小题考查，也能作为工具进行运用，这部分的主要结论有(1)当f(x)，g(x)同为增(减)函数时，f(x)＋g(x)则为增(减)函数.(2)奇函数在对称的两个区间上有相同的单调性，偶函数在对称的两个区间上有相反的单调性.(3)f(x)为奇函数⇔f(x)的图像关于原点对称；f(x)为偶函数⇔f(x)的图像关于y轴对称.(4)定义在(－∞，＋∞)上的奇函数的图像必过原点即有f(0)＝0.存在既是奇函数，又是偶函数的函数f(x)＝0.(5)f(x)＋f(－x)＝0⇔f(x)为奇函数；f(x)－f(－x)＝0⇔f(x)为偶函数.(6)若f(x)为偶函数，则f(x)＝f(－x)＝f(|x|).2.利用奇偶函数和单调性的定义和一些重要的结论，进行分析问题，提高逻辑思维和数学运算的素养.(1)判断f(x)的奇偶性；函数f(x)的定义域为(－∞，0)∪(0，＋∞)，所以函数f(x)是奇函数.(2)当x∈(1，＋∞)时，判断f(x)的单调性并证明；函数f(x)在(1，＋∞)上单调递增.证明如下：任取x1，x2∈(1，＋∞)，且x1x1>1，所以x1－x2<0，x1x2>0，x1x2－1>0，所以f(x1)－f(x2)<0，即f(x1)f(5－2m)，求m的取值范围.由(2)知函数f(x)在(1，＋∞)上单调递增，所以3m>5－2m>1，解得10， >0等.(2)函数的奇偶性的主要用途是实现函数值f(a)，f(－a)的转化，注意其图像的对称性的应用.(1)求实数m和n的值；∵f(x)是奇函数，∴f(－x)＝－f(x)，比较得n＝－n，n＝0.因此，实数m和n的值分别是2和0.(2)求函数f(x)在区间[－2，－1]上的最值.任取x1，x2∈[－2，－1]，且x1≠x2，∵x1，x2∈[－2，－1]且x1≠x2，∴函数f(x)在[－2，－1]上为增函数，函数图像的画法及应用 四1.利用函数的图像可以直观地观察函数的值域、最值、单调性、奇偶性等，重点是一次函数、二次函数、反比例函数等.2.掌握简单的基本函数图像，提升直观想象素养.(1)求实数m的值；当x<0时，－x>0，f(－x)＝－(－x)2＋2(－x)＝－x2－2x.又因为f(x)为奇函数，所以f(－x)＝－f(x)，所以当x<0时，f(x)＝x2＋2x，则m＝2.(2)画出函数的图像；函数f(x)的图像如图所示.(3)若函数f(x)在区间[－1，|a|－2]上单调递增，试确定a的取值范围.由图像可知f(x)在[－1,1]上单调递增，要使f(x)在[－1，|a|－2]上单调递增，只需－1<|a|－2≤1，即1<|a|≤3，解得－3≤a<－1或1