人教B版数学必修1 章末整合第三章 PPT课件

这是一份人教B版数学必修1 章末整合第三章 PPT课件，共43页。

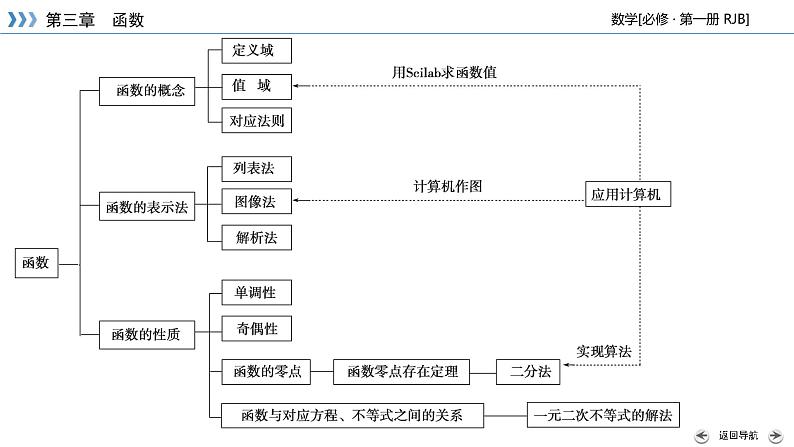
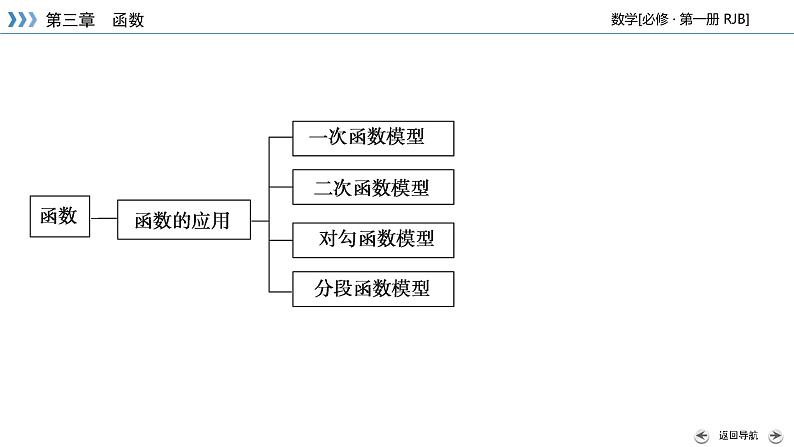
第三章函数章 末 整 合知识结构·理脉络要点梳理·晰精华1．函数的定义初中所学习的函数传统定义与高中的近代定义之间的异同点如下：[不同点]传统定义从变量变化的角度，刻画两个变量之间的对应关系；而近代定义，则从集合间的对应关系来刻画两个非空数集间的对应关系．[相同点]两种对应关系满足的条件是相同的，“变量x的每一个值”及“集合A中的每一个数”，都有唯一一个“y值”与之对应．2．函数三种表示方法的优缺点三种表示法的特点(优缺点)比较如下：4．函数单调性和奇偶性的重要结论(1)当f(x)，g(x)同为增(减)函数时，f(x)＋g(x)则为增(减)函数．(2)奇函数在对称的两个区间上有相同的单调性，偶函数在对称的两个区间上有相反的单调性．(3)f(x)为奇函数⇔f(x)的图像关于原点对称；f(x)为偶函数⇔f(x)的图像关于y轴对称．(4)偶函数的和、差、积、商是偶函数，奇函数的和、差是奇函数，积、商是偶函数，奇函数与偶函数的积、商是奇函数．(5)定义在(－∞，＋∞)上的奇函数的图像必过原点即有f(0)＝0.存在既是奇函数，又是偶函数的函数f(x)＝0.(6)f(x)＋f(－x)＝0⇔f(x)为奇函数；f(x)－f(－x)＝0⇔f(x)为偶函数．5．函数的零点(1)函数零点的定义对于函数y＝f(x)(x∈D)，使f(x)＝0的实数x称为函数y＝f(x)(x∈D)的零点．(2)几个等价关系方程f(x)＝0有实数根⇔函数y＝f(x)的图像与x轴有交点⇔函数y＝f(x)有零点．(3)函数零点的判定如果函数y＝f(x)在区间[a，b]上的图像是连续不断的一条曲线，并且有f(a)·f(b)＜0，那么，函数y＝f(x)在区间(a，b)内有零点，即存在c∈(a，b)，使得f(c)＝0，这个c也就是方程f(x)＝0的根．素养突破·提技能1．二次函数 已知函数f(x)＝ax2－2ax＋2＋b(a＞0)在区间[2,3]上的值域为[2,5]．(1)求a，b的值；(2)若关于x的函数g(x)＝f(x)－(m＋1)x在区间[2,4]上为单调函数，求实数m的取值范围．典例 1思路探究：(1)二次函数固定区间上求值域，要先判断对称轴与区间端点的关系；(2)单调函数分单调递增和递减两种情况讨论．归纳提升：解决二次函数在某区间上的最值问题，关键是对函数图像的对称轴与给定区间的相对位置关系进行讨论，一般分为对称轴在区间的左侧、内部、右侧三种情况求解．二次函数的单调性和最值问题是本章的重点知识．2．分段函数典例 2归纳提升：分段函数在函数中占有重要的地位，对分段函数的问题要注意以下几点：(1)分段函数的图像问题、求分段函数的解析式、求分段函数的单调区间、求分段函数的值域或最值、解分段函数对应的方程或不等式等的解法均可归纳为“分段处理”四个字．(2)分段函数的求值、分段函数的奇偶性判断，要严格按照分段函数的含义及奇偶性的定义来处理．3．对勾函数典例 31．函数的单调性与奇偶性的综合应用典例 4归纳提升：有关函数奇偶性与单调性的综合问题，主要有比较函数值的大小、解不等式等，关键是利用奇、偶函数的对称性，将不在同一单调区间上的两个自变量的值转化到同一单调区间上，再利用函数的单调性来处理，使问题得以解决．2．函数的零点与方程根的关系及应用 设a∈R，关于x的一元二次方程7x2－(a＋13)x＋a2－a－2＝0有两个实数根x1，x2，且0＜x1＜1＜x2＜2.求a的取值范围．思路探究：令f(x)＝7x2－(a＋13)x＋a2－a－2，其图像是开口向上的抛物线，它在(0,1)和(1,2)区间内与x轴相交，则有f(0)＞0，f(1)＜0，f(2)＞0.典例 5归纳提升：抓住三个二次之间的关系是解此题的关键，将一元二次方程根的分布问题转化为函数零点问题．函数零点的应用主要是利用函数零点存在定理求参数值或范围，体现化归转化思想，数形结合思想．真题精练·悟考情1．(2019·全国 Ⅱ文数)设f(x)为奇函数，且当x≥0时，f(x)＝ex－1，则当x＜0时，f(x)＝ (　　)A． e－x－1　 B． e－x＋1　　C． －e－x－1　 D． －e－x＋1解析：当x＜0时，－x＞0，f(－x)＝e－x－1，又f(x)为奇函数，有f(x)＝－f(－x)＝－e－x＋1.D 　 解析：由题意得到关于x的不等式，解不等式可得函数的定义域．由已知得7＋6x－x2≥0 ，即x2－6x－7≤0，解得－1≤x≤7，故函数的定义域为[－1,7]．[－1,7]　3．(2019·北京理数改编)设函数f(x)＝ex＋ae－x(a为常数)．若f(x)为奇函数，则a＝______.解析：首先由奇函数的定义得到关于a的恒等式，据此可得a的值．若函数f(x)＝ex＋ae－x为奇函数，则f(－x)＝－f(x)，即e－x＋aex＝－(ex＋ae－x)，即(a＋1)(ex＋e－x)＝0对任意的x恒成立，则a＋1＝0，得a＝－1.－1　B 　 如图：