北师大版七年级数学上册第4章综合检测卷课件

这是一份北师大版七年级数学上册第4章综合检测卷课件，共37页。

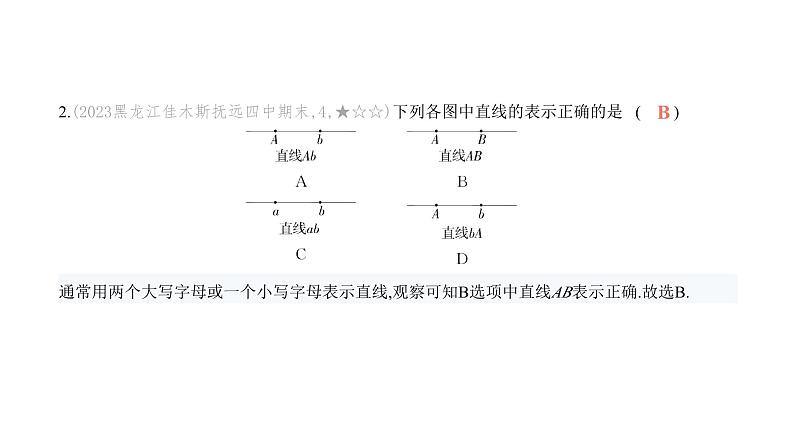
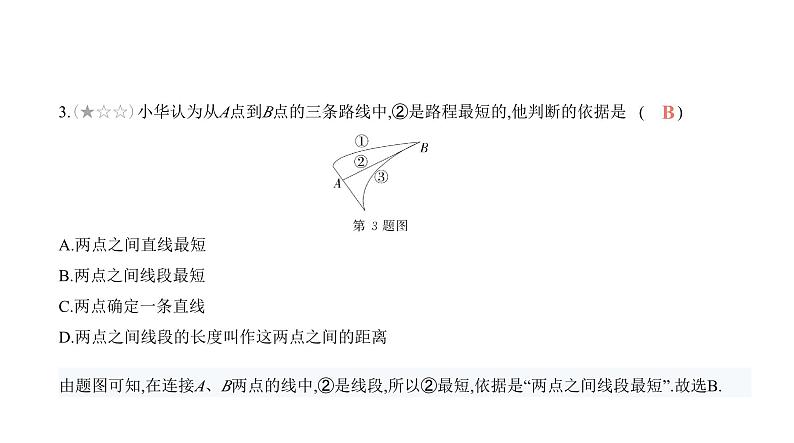
第四章　综合检测卷(时间：90分钟 满分：120分)考查内容：基本平面图形一、选择题(本大题共10小题,每小题3分,共30分)1.(新独家原创,★☆☆)下列说法正确的是 (　　)A.线段AB和线段BA是同一条线段B.射线AB和射线BA是同一条射线C.直线AB与直线BA不是同一条直线D.以上说法都正确A2.(2023黑龙江佳木斯抚远四中期末,4,★☆☆)下列各图中直线的表示正确的是 (　　) 　　      　　      B通常用两个大写字母或一个小写字母表示直线,观察可知B选项中直线AB表示正确.故选B.3.(★☆☆)小华认为从A点到B点的三条路线中,②是路程最短的,他判断的依据是 (　　) A.两点之间直线最短　　　    B.两点之间线段最短C.两点确定一条直线　　　    D.两点之间线段的长度叫作这两点之间的距离B由题图可知,在连接A、B两点的线中,②是线段,所以②最短,依据是“两点之间线段最短”.故选B.4.(2024河南驻马店确山期中,5,★☆☆)过某个多边形一个顶点的所有对角线,将这个多边形分成八个三角形,这个多边形是 (　　)A.七边形　　　    B.八边形　　　    C.九边形　　　    D.十边形D过n边形一个顶点引对角线,可将多边形分割成(n-2)个三角形,因为n-2=8,所以n=10,即这个多边形是十边形,故选D.5.(2024河北邯郸永年期中改编,9,★☆☆)下列各式中,正确的是 (　　)A.35°50'=35.5°　　　    B.15°12'36″=15.48°C.28°18'18″=28.33°　　　    D.65°15'=65.25°D35.5°=35°30',15°12'36″=15.21°,28°18'18″=28.305°,65°15'=65.25°.故选D.6.(2023山东乳山怡园中学期末,3,★★☆)如图,将一个圆分成甲、乙、丙三个扇形,其圆心角度数之比为2∶3∶4.若圆的半径为3,则扇形乙的面积为 (　　) A. π　　　    B. π　　　    C.3π　　　    D.4πC7.(2023甘肃兰州三十五中期末,6,★★☆)如图所示,点B在点O的北偏东60°方向,射线OB与射线OC所成的角是115°,则射线OC的方向是 (　　) A.北偏西35°　　　    B.北偏西55°C.北偏西60°　　　    D.西偏北55°B因为射线OC与射线OB所成的角是115°,所以∠COB=115°.因为点B在点O的北偏东60°方向,所以射线OB与正北方向线所成的角是60°,所以射线OC与正北方向线所成的角是115°-60°=55°,所以射线OC的方向是北偏西55°.故选B.8.(★★☆)如图,点C、D分别是线段AB上的点(CD>AC,CD>BD),用圆规在线段CD上截取CE=AC,DF=BD,若点E与点F恰好重合,AB=8,则CD= (　　) A.4　　　    B.4.5　　　    C.5　　　    D.5.5A9.(2024黑龙江齐齐哈尔依安期末,10,★★☆)已知∠AOC=100°,过点O作射线OB,OM,使∠AOB=30°,OM是∠BOC的平分线,则∠AOM的度数为     (　　)A.35°　　　    B.35°或65°　　　    C.40°或65°　　　    D.65°B      如图2所示,射线OB在∠AOC外部,因为∠AOC=100°,∠AOB=30°,所以∠BOC=∠AOC+∠AOB=130°.因为OM是∠BOC的平分线,所以∠BOM= ∠BOC=65°,所以∠AOM=∠BOM-∠AOB=35°.综上所述,∠AOM=35°或∠AOM=65°,故选B.易错警示本题求角度,题目没有给出图形,求解时应根据可能存在的情况分别画出图形求解,避免漏解.10. 学科素养　模型观念    (2023山东聊城月考,4,★★☆)某高铁线共设有5个站点,要保证每两个站点之间都有票可买,需要印制不同的火车票 (　　)A.20种　　　    B.42种　　　    C.10种　　　    D.84种A二、填空题(本大题共6小题,每小题4分,共24分)11.(★☆☆)已知不在同一直线上的两条线段AB和CD,李明很难判断出它们的长短,因此他借助圆规,操作如图所示,由此可得出AB　　　    CD(填“>”“<”或“=”).>12. 学科素养　模型观念    (★☆☆)如图,在一张零件图中,已知AD=35 mm,BD=32 mm,CD=9 mm,则AB=　　　    mm,BC=　　　    mm.  323因为AD=35 mm,BD=32 mm,所以AB=AD-BD=35-32=3(mm).因为BD=32 mm,CD=9 mm,所以BC=BD-CD=32-9=23(mm).13.(2023北京东城期末,13,★☆☆)在如图所示的由小正方形组成的网格中,点A,B,C,D,O均在格点(小正方形的顶点)上,那么∠AOC　　　    ∠BOD(填“>”“<”或“=”).  <如图,∠BOD=∠AOE,∵∠AOC<∠AOE,∴∠AOC<∠BOD.  14.(2023山东淄博张店期末,12,★★☆)早睡早起习惯好,小明养成了晚上9:00左右睡觉的好习惯.某天晚上小明睡觉前看了一下时间,是9:20,此时时钟上的分针与时针所成的角的度数是　　        .160°方法解读示意图法求钟面上的角度计算时针与分针夹角的度数,通常先画出示意图,借助图形及时针每分钟转过0.5°,分针每分钟转过6°进行和差计算.15.(★★☆)线段AB上有P、Q两点,AB=26,AP=14,PQ=11,那么BQ=　　　    .23或116.(2023陕西省西安爱知中学期末改编,12,★★☆)一副三角板按如图所示的方式摆放,点A,P,D在同一条直线上,将三角板ABP绕点P以每秒10°的速度顺时针旋转,当边PB落在边PD上时停止旋转,在旋转过程中,若PB平分∠APC,则三角板ABP旋转的时间是　　　    秒.  3由题意得∠APB=45°,∠CPD=60°,当PB在∠CPD外,在∠APC内时,BP才有可能平分∠APC,所以PB平分∠APC时,∠CPB=∠APB=45°.三角板ABP旋转的角度为180°-∠CPB-∠APB-∠CPD=180°-45°-45°-60°=30°.因为三角板ABP绕点P以每秒10°的速度顺时针旋转,所以三角板ABP运动的时间是30÷10=3(秒).三、解答题(共66分)(含评分细则)17.(10分)(★☆☆)如图,在平面内有A,B,C三点.(1)作直线AB、射线AC、线段BC;(2)在线段BC上任取一点D(不同于点B,C),连接AD,并延长AD至点E,使DE=AD;(3)在前两问的基础上,此时图中的线段共有　　　    条.第17题图(1)如图,直线AB、射线AC、线段BC即为所求. (3分)(2)如图,点D在BC上位置不固定. (6分)(3)8. (10分)提示:图中的线段有AB,AC,AD,AE,DE,BD,CD,BC,共8条.18. 新考向　尺规作图    (10分)(★☆☆)如图,已知∠α和点O.利用直尺和圆规画∠AOB,使∠AOB=180°-2∠α(保留作图痕迹,不写作法).      如图,先作平角∠COD,再在CD上方分别作∠AOC=∠α,∠BOD=∠α,则∠AOB即为所作.  (10分)19.(10分)(2023山东省蓬莱第一中学期中,20,★★☆)如图,圆O的直径为10 cm,两条直径AB,CD相交成90°角,∠AOE=50°,OF是∠BOE的平分线.(1)求圆心角∠COF的度数;(2)求扇形COF的面积.  (1)因为∠AOB=180°,∠AOE=50°,所以∠BOE=180°-50°=130°. (2分)因为OF是∠BOE的平分线,所以∠BOF= ∠BOE=65°. (4分)因为两条直径AB,CD相交成90°角,所以∠COF=90°-65°=25°. (6分)(2)因为圆O的面积=52π=25π cm2, (8分)所以扇形COF的面积=25π× = π cm2. (10分)20.(11分)(★★☆)如图,已知线段AB=23,BC=15,点M是AC的中点.(1)求线段AM的长;(2)在CB上取一点N,使得CN∶NB=1∶2,求线段MN的长.  (1)因为AB=23,BC=15,所以AC=AB-BC=23-15=8. (2分)又因为点M是AC的中点,所以AM= AC= ×8=4,即线段AM的长是4. (5分)(2)因为BC=15,CN∶NB=1∶2,所以CN= BC= ×15=5. (8分)因为点M是AC的中点,AC=8,所以MC= AC=4,所以MN=MC+NC=4+5=9. (11分)21.(11分)(★★☆)【观察思考】如图,五边形ABCDE内部有若干个点,用这些点以及五边形ABCDE的顶点A、B、C、D、E把原五边形分割成一些三角形(互不重叠). 【规律总结】(1)填写下表:【问题解决】(2)原五边形能被分割成2 025个三角形吗?若能,求此时五边形ABCDE内部有多少个点;若不能,请说明理由.(1)从左到右答案为11;2n+3. (5分)提示:因为五边形ABCDE内点的个数为1时,分割成的三角形的个数为5=2×1+3,五边形ABCDE内点的个数为2时,分割成的三角形的个数为7=2×2+3,五边形ABCDE内点的个数为3时,分割成的三角形的个数为9=2×3+3,所以五边形ABCDE内点的个数为4时,分割成的三角形的个数为2×4+3=11,……所以五边形ABCDE内点的个数为n时,分割成的三角形的个数为2n+3.(2)原五边形能被分割成2 025个三角形. (7分)由题意得2n+3=2 025,因为2 022+3=2 025,所以2n=2 022. (9分)所以n=1 011,符合实际.所以原五边形能被分割成2 025个三角形,此时内部有1 011个点. (11分)22. 学科素养　推理能力    (14分)(2023山西运城稷山中学期末,23,★★★)综合与实践.问题情境:(1)数学活动课上,老师和同学们借助一副三角板的拼摆来发现问题.先按照图①的方式摆放,画出∠AOB;再按照图②的方式在∠AOB内摆放一副三角尺,画出射线OC,则∠AOB=　　　    °,∠AOC=　　　    °,射线OC是∠AOB的　　　    . 猜想推广:(2)①小强同学说借助一副三角板的拼摆能画出15°的角,请回答是“相信”还是“不信”.②智慧小组经过讨论后发现:设一个角可以由30°角和45°角分别重复画m次和n次合并而成(m,n是整数),若这个角的度数为a°,则a=30m+45n,可见借助一副三角板的拼摆,还能画出很多角.请在智慧小组讨论的基础上回答:这些角的度数能被15整除吗?具体问题:(3)奋进小组提出了一个新问题,如图③,已知同一平面内,∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC.求∠DOE的度数.发现特性:(4)创新小组在老师的启发下又进行了深入探究,在(3)的条件下,如果将题目中∠AOC=60°改成∠AOC=2α(α<45°),其他条件不变,他们有了“∠DOE的度数为定值”的重大发现.请帮他们写出这个重大发现的求解过程.(1)150;75;平分线. (3分)提示:根据“三角板”中各个角的度数以及题图①的拼图方法可知∠AOB=90°+60°=150°,由题图②的拼图方法可知∠AOC=150°-(30°+45°)=75°.因为∠AOC=75°= ∠AOB,所以OC是∠AOB的平分线.(2)①相信. (5分)提示:可以利用三角板的内角度数差为15°画出15°的角,如:60°-45°=15°=45°-30°.②这些角的度数能被15整除,理由:a=30m+45n=15(2m+3n),因此这些角的度数能被15整除. (7分)(3)因为∠AOB=90°,∠AOC=60°,所以∠BOC=90°+60°=150°. (9分)因为OD平分∠BOC,OE平分∠AOC,所以∠BOD=∠COD= ∠BOC=75°,∠AOE=∠COE= ∠AOC=30°,所以∠DOE=∠COD-∠COE=75°-30°=45°. (11分)(4)因为∠AOB=90°,∠AOC=2α,所以∠BOC=90°+2α. (12分)因为OD平分∠BOC,OE平分∠AOC,所以∠BOD=∠COD= ∠BOC= (90°+2α)=45°+α,∠AOE=∠COE= ∠AOC=α,所以∠DOE=∠COD-∠COE=45°+α-α=45°. (14分)