





北师大版八年级上册第四章 一次函数1 函数教学演示ppt课件
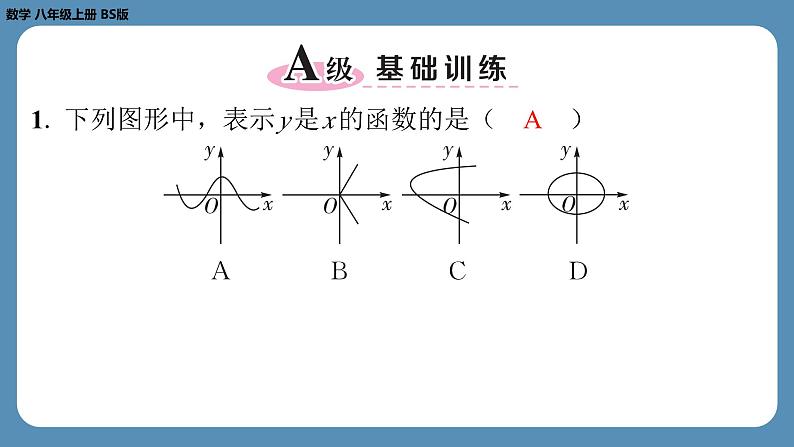
展开1. 下列图形中,表示 y 是 x 的函数的是( A )
2. 下列变量中, y 不是 x 的函数的是( C )
3. 已知A,B两地相距3km,小黄从A地走到B地,平均速度为 4km/h.若用 x (h)表示行走的时间, y (km)表示余下的路 程,则 y 与 x 之间的关系式是( D )
5. (1)已知高度每升高1km,气温就下降6℃,则降低的温度 T (℃)与升高的高度 h (km)之间的关系式为 ;(2)如图,在长方形 ABCD 中, AD =10cm, AB =4cm,点 P 是边 AD 上一点(不与点 D 重合).设 AP 的长为 x cm,△ PCD 的 面积为 S cm2,则 S 与 x 之间的关系式为 .
T =6 h ( h >
S =20-2 x (0≤ x <
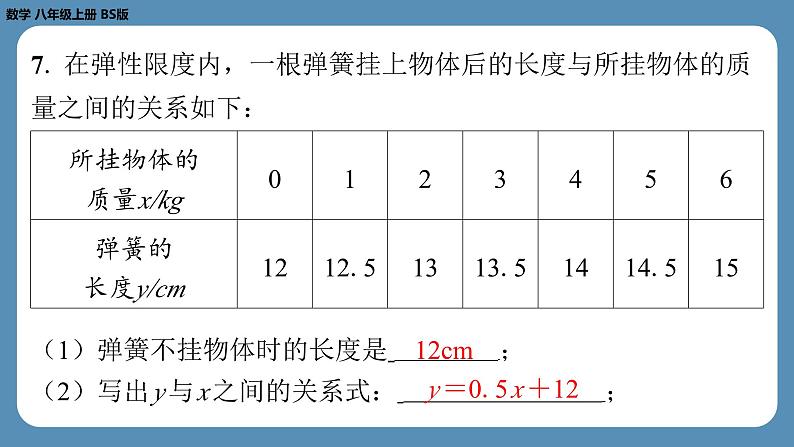
7. 在弹性限度内,一根弹簧挂上物体后的长度与所挂物体的质 量之间的关系如下:
(1)弹簧不挂物体时的长度是 ;(2)写出 y 与 x 之间的关系式: ;
y =0.5 x +12
(3)当所挂物体的质量为14kg时,弹簧的长度是多少厘米?
(3)解:当 x =14时, y =0.5×14+12=19(cm).所以当所挂物体的质量为14kg时,弹簧的长度是19cm.
8. 小丁每天从报社以每份0.5元的价格买进报纸200份,然后以 每份1元的价格卖给读者,报纸卖不完,当天可退回报社,但报 社只按每份0.2元退费给小丁.设小丁平均每天卖出报纸 x 份,纯 收入为 y 元.(1)求 y 与 x 之间的关系式(写出自变量 x 的取值范围);
(2)若每月按30天计算,则小丁每天至少要卖多少份报纸才能 使每月纯收入达到2 000元?
解:(1)由题意,得 y =(1-0.5) x -(0.5-0.2)·(200- x )=0.8 x -60.故 y =0.8 x -60(0≤ x ≤200,且 x 为整数).
9. 小明晚饭后出门散步,从家(点 O )出发,最后回到家里, 行走的路线如图中箭头所示.小明离家的距离 h 与散步时间 t 之 间的函数关系可能是( C )
10. 如图,根据该程序计算函数 y 的值,若输入 x 的值是7,则输 出 y 的值是-2.若输入 x 的值是-8,则输出 y 的值是 .
11. 国庆节期间,小华约同学一起开车到距家100km的景点旅 游.出发前,汽车油箱内储油35L,行驶80km后,发现油箱内剩 余油量为25L(假设行驶过程中汽车的耗油量是均匀的).(1)求该车平均每千米的耗油量,并写出出发后油箱内剩余油 量 Q (L)与行驶路程 x (km)之间的关系式(写出自变量的取 值范围).(2)当 x =60时,求油箱内剩余的油量.
(3)当油箱中剩余油量低于3L时,汽车将自动报警.如果往返 途中不加油,他们能否在汽车报警前回到家?请说明理由.
解:(1)由题意,得该汽车平均每千米的耗油量为(35-25) ÷80=0.125(L).出发后油箱内剩余油量 Q (L)与行驶路程 x (km)之间的关系式为 Q =35-0.125 x (0≤ x ≤280).
(2)当 x =60时, Q =35-0.125×60=27.5.故当 x =60时,油箱内剩余的油量为27.5L.
(3)他们能在汽车报警前回到家.理由如下:因为(35-3)÷0.125=256(km),256≥200,所以他们能在汽车报警前回到家.
12. 为了加强公民的节水意识,合理利用水资源,各地采用价 格调控手段达到节约用水的目的,某市规定用水收费标准如 下:每户每月的用水量不超过6m3时,水费按每立方米 a 元收 费;超过6m3时,不超过的部分每立方米仍按 a 元收费,超过的 部分按每立方米 b 元收费.该市小明家去年9月份、10月份的用 水量和所交水费如下表所示:
设小明家每月用水量为 x (m3),应交水费为 y (元).(1) a = , b = ;(2)求 y 与 x 之间的关系式;
(3)若小明家去年11月份、12月份的用水总量为14m3,共交水 费27元(11月份的用水量小于12月份的用水量),分别求小明 家11月份、12月份的用水量.
(3)解:因为小明家11月份、12月份的用水总量为14m3,11月 份的用水量小于12月份的用水量,所以12月份的用水量大于7m3.设12月份的用水量为 m m3,则11月份的用水量为(14- m )m3.
①当7< m ≤8时,3 m -9+3(14- m )-9=27.此方程无解.
②当8< m <14时,3 m -9+1.5(14- m )=27,
解得 m =10.故小明家11月份的用水量为4m3,12月份的用水量为10m3.
13. (选做)如图1,在长方形 ABCD 中,动点 P 从点 B 出发, 沿 BC , CD , DA 运动至点 A 停止.设点 P 运动的路程为 x ,△ ABP 的面积为 y , y 关于 x 的函数图象如图2所示.(1)求长方形 ABCD 的面积;(2)求点 M , N 的坐标;
解:(1)结合图形可以知,当点 P 在 BC 上时,△ ABP 的面积 y 在增大,当 x 在4和9之间时,△ ABP 的面积不变,得出 BC =4, CD =5.所以长方形 ABCD 的面积为4×5=20.
北师大版八年级上册6 实数图片ppt课件: 这是一份北师大版八年级上册<a href="/sx/tb_c10028_t3/?tag_id=26" target="_blank">6 实数图片ppt课件</a>,共20页。PPT课件主要包含了无理数集,整数集,解1填写如下等内容,欢迎下载使用。
北师大版八年级上册4 估算课堂教学ppt课件: 这是一份北师大版八年级上册<a href="/sx/tb_c91894_t3/?tag_id=26" target="_blank">4 估算课堂教学ppt课件</a>,共18页。PPT课件主要包含了-10或1,>b>c等内容,欢迎下载使用。
初中北师大版3 立方根课堂教学ppt课件: 这是一份初中北师大版<a href="/sx/tb_c10025_t3/?tag_id=26" target="_blank">3 立方根课堂教学ppt课件</a>,共19页。













