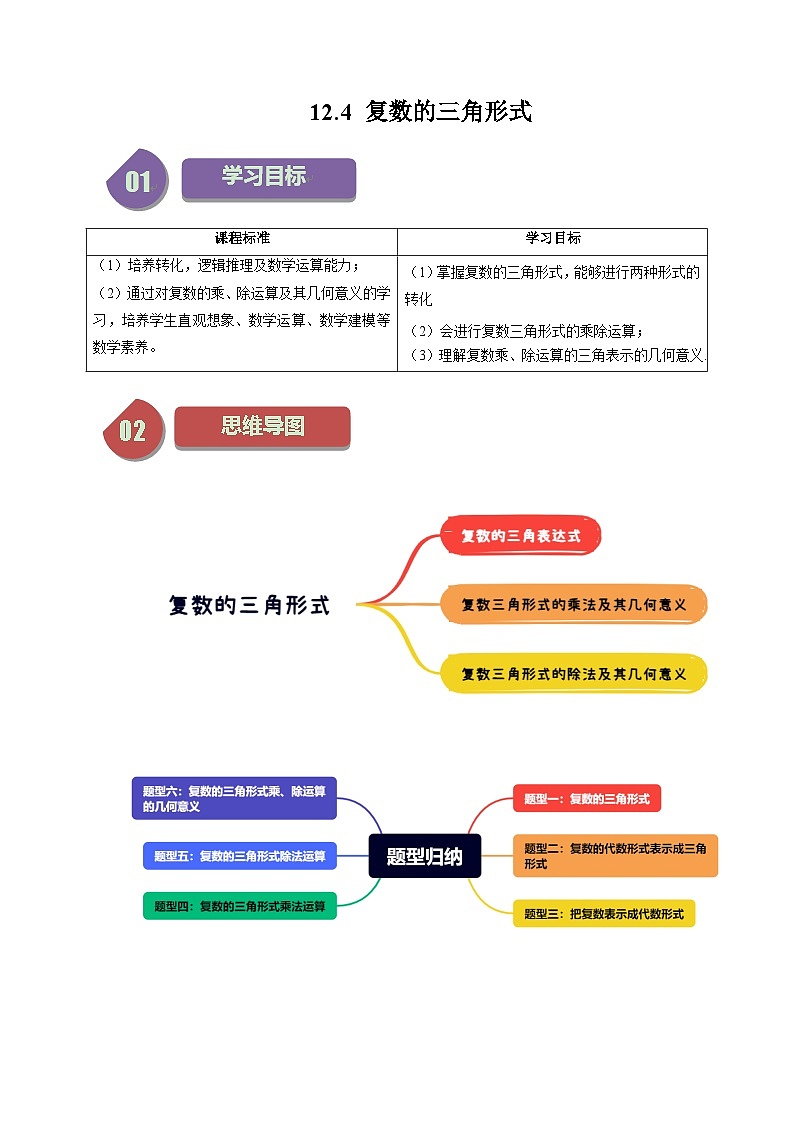
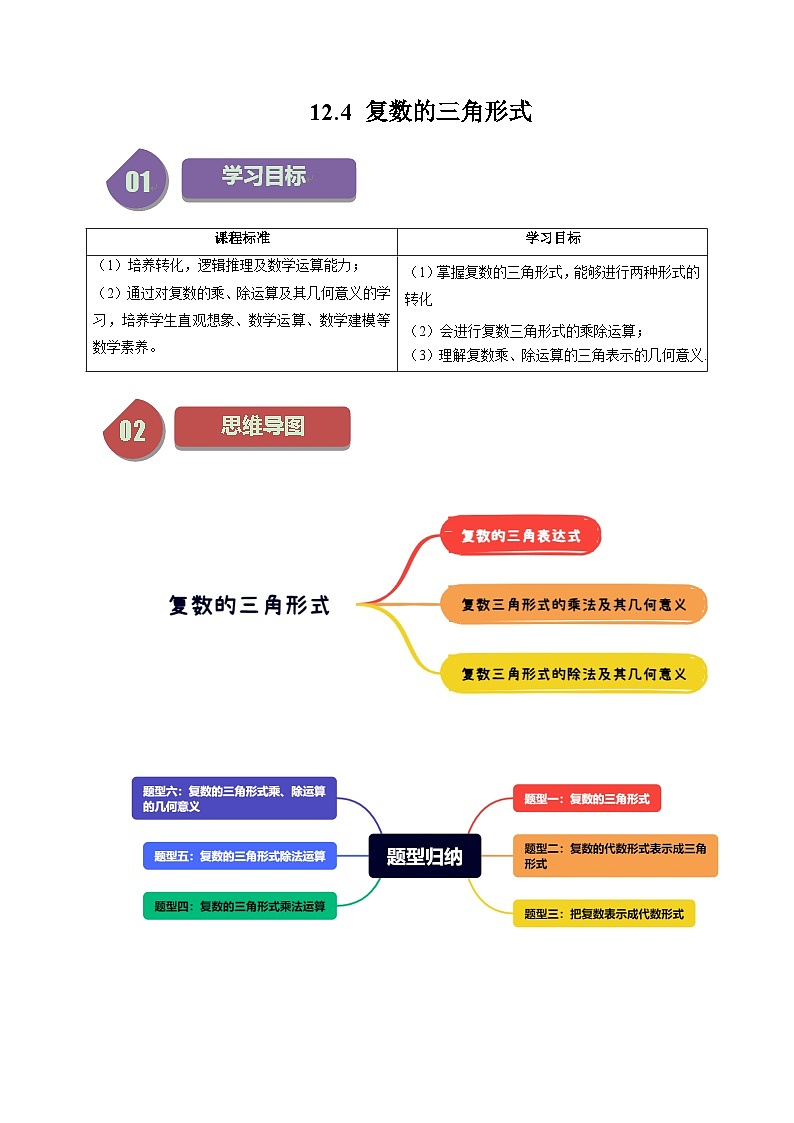
苏教版 (2019)必修第二册12.4 复数的三角形式精品课堂检测

展开

这是一份苏教版 (2019)必修第二册12.4 复数的三角形式精品课堂检测，文件包含124复数的三角形式六大题型练习原卷高中数学苏教版必修二docx、124复数的三角形式六大题型练习解析卷高中数学苏教版必修二docx等2份试卷配套教学资源，其中试卷共37页，欢迎下载使用。

知识点01 复数的三角形式
1、复数的辐角
以轴的正半轴为始边、向量OZ所在的射线为终边的角，叫做复数的辐角．
适合于的辐角的值，叫辐角的主值．记作：，即．
2、复数的三角表达式
一般地，任何一个复数都可以表示成的形式．其中，是复数的模；是复数的辐角．叫做复数的三角表示式，简称三角形式．为了与三角形式区分开来叫做复数的代数表示式，简称代数形式．
注意：复数三角形式的特点
模非负，角相同，余弦前，加号连
3、两个用三角形式表示的复数相等的充要条件：
两个非零复数相等当且仅当它们模与辐角的主值分别相等．
【即学即练1】（2024·高一·全国·课时练习）的三角形式是．
【答案】（答案不唯一）
【解析】令且，
所以，则满足，
所以三角形式可写成.
故答案为：(答案不唯一)
知识点02 复数的三角形式乘、除运算
1、复数三角形式的乘法及其几何意义
设、的三角形式分别是：，．
则．
简记为：模数相乘，幅角相加
几何意义：把复数对应的向量绕原点逆时针旋转的一个辐角，长度乘以的模，所得向量对应的复数就是．
2、复数三角形式的除法及其几何意义
设、的三角形式分别是：，．
则．
简记为：模数相除，幅角相减
几何意义：把复数对应的向量绕原点顺时针旋转的一个辐角，长度除以的模，所得向量对应的复数就是．
【即学即练2】复数的值是（）
A．B．16C．D．
【答案】A
【解析】.
故选：A
题型一：复数的三角形式
【典例1-1】（2024·高一课时练习）下列各式中已表示成三角形式的复数是（）.
A．B．
C．D．
【答案】B
【解析】复数的三角表示为：，其中，B选项满足.
故选：B.
【典例1-2】（2024·高一课时练习）复数在复平面对应的点绕原点逆时针旋转所得点对应的复数为（）
A．B．C．D．
【答案】B
【解析】，将复数在复平面对应的点绕原点逆时针旋转，
可得.
故选：B
【变式1-1】（2024·高一课时练习）复数改写成三角形式，正确的是（）
A．B．
C．D．
【答案】B
【解析】∵，
，，
又，∴，
∴
故选：B．
【变式1-2】（2024·高一·全国·随堂练习）判断下列复数是不是复数的三角形式，并说明理由.
(1)；
(2)．
【解析】（1）括号内两项中间不是加号，故不是复数的三角形式，
其三角形式为.
（2）不满足复数的模大于等于0，故不是复数的三角形式，
其三角形式为.
【方法技巧与总结】
解题总结（复数三角形式的判断依据和变形步骤）
（1）判断依据：三角形式的结构特征：模非负，角相同，余弦前，加号连．
（2）变形步骤：首先确定复数z对应点所在象限（此处可假定θ为锐角），其次判断是否要变换三角函数名称，最后确定辐角．此步骤可简称为“定点→定名→定角”．
题型二：复数的代数形式表示成三角形式
【典例2-1】（2024·高一·全国·课时练习）把复数（i为虚数单位）改写成三角形式为．
【答案】
【解析】由题可得，且在第三象限，
所以辐角的主值为，
所以，
故答案为：.
【典例2-2】（2024·高一·全国·课时练习）将复数表示成三角形式是．（用辐角主值）
【答案】
【解析】令且，
则，故，
所以.
故答案为：
【变式2-1】（2024·高一·全国·课时练习）（）改写成三角形式为．
【答案】当时，复数的三角形式可以为（答案不唯一）；当时，复数的三角形式可以为（答案不唯一）；当时，复数的三角形式可以为（答案不唯一）.
【解析】复数的模为，设复数的辐角为，
当时，复数的模为，，，则，，
此时复数的三角形式可以为，
当时，复数的三角形式为，
当时，复数的模为，，，则，，
此时复数的三角形式可以为，
故答案为：当时，复数的三角形式可以为（答案不唯一）；当时，复数的三角形式可以为（答案不唯一）；当时，复数的三角形式可以为（答案不唯一）.
【变式2-2】（2024·高一·上海闵行·期末）将复数化为三角形式：．
【答案】
【解析】复数中，，设为复数的辐角主值，
又
所以.
故答案为：.
【方法技巧与总结】
解题总结：（复数的代数形式化三角形式的步骤）
（1）先求复数的模；
（2）决定辐角所在的象限；
（3）根据象限求出辐角（常取它的主值）；
（4）写出复数的三角形式．
题型三：把复数表示成代数形式
【典例3-1】（2024·高一·全国·课前预习）将复数z＝化为代数形式为．
【答案】1－i
【解析】z＝．
故答案为：1－i
【典例3-2】（2024·高一·全国·课时练习）复数10表示成代数形式为．
【答案】－5－5i/－5i－5
【解析】10＝10＝－5－5i．
故答案为：
【变式3-1】（2024·高一·全国·课时练习）设复数，那么的共轭复数的代数形式是．
【答案】/-i+
【解析】，故.
故答案为：.
【变式3-2】（2024·高一·全国·课时练习）将复数z=3化成代数形式为 ;|z|= .
【答案】 3
【解析】，
故答案为：
【变式3-3】（2024·高一·全国·课时练习）将复数化为代数形式为
【答案】
【解析】由题得.
故答案为：
【方法技巧与总结】
解题总结（把复数表示成代数形式的注意事项）
（1）类似三角形式的复数求模和辐角时，注意三角形式的结构特征：模非负，角相同，余弦前，加号连．
（2）由三角形式表示成代数形式，直接求出角的三角函数值，化简即可．
题型四：复数的三角形式乘法运算
【典例4-1】（2024·高一·全国·课时练习）如果，那么复数的三角形式是（）
A．
B．
C．
D．
【答案】A
【解析】因为，，
所以.
故选：A.
【典例4-2】（2024·高一·湖北武汉·期末）已知i为虚数单位，则（）
A．B．1C．D．i
【答案】D
【解析】
故选：D
【变式4-1】（2024·高一·江苏盐城·期末）欧拉公式（为自然对数的底数，为虚数单位）由瑞士数学家（欧拉）首先发现.它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，被称为“数学中的天桥”，则下列运算一定正确的是（）
A．
B．
C．
D．
【答案】C
【解析】.
故选：C.
【变式4-2】（2024·高三·北京·强基计划）已知复数z满足，则中不同的数有（）
A．4个B．6个C．2019个D．以上答案都不正确
【答案】B
【解析】根据题意，有，
于是中有6个不同的数．
故选：B.
【变式4-3】（2024·高一·全国·课时练习）计算的值是（）
A．B．
C．D．
【答案】B
【解析】因为
所以，
所以，
故选：B.
【变式4-4】（2024·高一·全国·课时练习）已知为虚数单位，，，则等于（）
A．B．
C．D．
【答案】D
【解析】，
.
故选：D.
【方法技巧与总结】
解题总结（复数的三角形式乘法运算的注意事项）
两个复数相乘，积还是一个复数，它的模等于各复数的模的积，它的幅角等于各复数的幅角的和．简单的说，两个复数三角形式相乘的法则为：模数相乘，幅角相加．
题型五：复数的三角形式除法运算
【典例5-1】（2024·高一·全国·课时练习）设复数，则得一个辐角是 .
【答案】（答案不唯一）
【解析】由题意得，
，
所以得辐角是（答案不唯一）
故答案为：（答案不唯一）
【典例5-2】（2024·高一·全国·专题练习）计算：．(用代数形式表示)
【答案】
【解析】.
故答案为：.
【变式5-1】（2024·高一·全国·课时练习） .
【答案】i/
【解析】根据复数的三角形式的运算法则，可得：
.
故答案为：
【变式5-2】（2024·高一·福建莆田·阶段练习），则 .
【答案】400
【解析】，
若，则，
∴.
故答案为：.
【变式5-3】（2024·高一·上海·单元测试）若，则的辐角主值为 .
【答案】
【解析】，辐角．
得的辐角主值.
故答案为：.
【变式5-4】（2024·高一·全国·课时练习）已知i为虚数单位，计算： .
【答案】
【解析】先把转化为，再利用复数三角形式的除法运算法则即可求出答案.原式
.
故答案为：.
【方法技巧与总结】
解题总结：（复数的三角形式除法运算的注意事项）
两个复数相除，商还是一个复数，它的模等于被除数的模除以除数的模，它的幅角等于被除数的辐角减去除数的辐角．简单的说切记两个复数三角形式除法运算法则：模数相除，幅角相减．
题型六：复数的三角形式乘、除运算的几何意义
【典例6-1】（2024·高一·全国·课时练习）在复平面内，把与复数对应的向量绕原点按逆时针方向旋转45°，所得向量对应的复数为，则复数是 .(用代数形式表示).
【答案】
【解析】由题意得.
故答案为：
【典例6-2】（2024·高一·全国·随堂练习）在复平面内，将与复数对应的向量绕原点O按顺时针方向旋转60°，求与所得的向量对应的复数，写出你的思考过程．
【解析】根据复数乘法的几何意义，所求的复数是，
即.
故与所得的向量对应的复数是.
【变式6-1】（2024·高一·全国·随堂练习）图中四边形ABCD，DCEF，FEGH都是正方形，用复数方法证明：．

【解析】以为坐标原点，以方向为轴的正方向建立平面直角坐标系，如下图所示：
令，可得点，
所以对应的复数分别为，
所以分别为的辐角，且；
可得
；
所以可得
【变式6-2】（2024·高一·全国·随堂练习）在复平面内，复数，，，它们对应的向量分别为、、，如何直观地理解与、与之间的位置关系呢？
【解析】因为，所以，，
，所以，，
所以，先将沿原方向伸长倍，再逆时针旋转，可得到，
将反向伸长为原来的倍，可得到.
【变式6-3】（2024·高一·全国·随堂练习）将复数对应的向量旋转，求所得向量对应的复数．
【解析】由题意，
旋转后，变为，
∴旋转后所得向量对应的复数为.
【变式6-4】（2024·高一·福建泉州·期中）已知复数已在复平面内对应的点在第一象限，是虚数单位.
(1)求实数的取值范围
(2)当时，求复数的三角表示
(3)若复平面内，向量对应（2）中的复数，把绕点顺时针方向旋转得到，求向量对应的复数（结果用代数形式表示）
【解析】（1）因为复数已在复平面内对应的点在第一象限，
所以，解得，所以实数的取值范围为：
（2）当时，，所以，，
所以，所以
（3）根据题意得，设其旋转后对应向量，
所以，解得或，
又因为绕点顺时针方向旋转得到，所以对应的点在第四象限，
所以，所以.
【变式6-5】（2024·高一·福建泉州·阶段练习）在复平面内，点A对应的复数是，向量绕着点O按逆时针方向旋转120°得到向量.
(1)求点C对应的复数；
(2)已知点B对应的复数z满足，且，求复数z.
【解析】（1）因为点A对应的复数是，向量绕着点O按逆时针方向旋转120°，
所以；
（2）因为点B对应的复数z满足，且，
所以向量对应的复数，
或，
∴或，
∴或.
【变式6-6】（2024·高一·全国·课时练习）如图，向量对应的复数为，把绕点O按逆时针方向旋转，得到，求向量对应的复数（用代数形式表示）.
【解析】向量对应的复数为
，
故答案为：.
【方法技巧与总结】
解题总结（复数的三角形式乘、除运算的几何意义的注意事项）
复数乘法几何意义是解题关键．把复数对应的向量绕原点逆时针旋转的一个辐角，长度乘以的模，所得向量对应的复数就是．
复数除法几何意义是解题关键．把复数对应的向量绕原点顺时针旋转的一个辐角，长度除以的模，所得向量对应的复数就是．
一、单选题
1．（2024·高三·全国·专题练习）复数的三角形式是（）
A．B．
C．D．
【答案】D
【解析】依题意，令，
则，所以，
因为，所以，
所以的三角形式是.
故选：D.
2．（2024·高一·福建厦门·期中）已知复数，则（）
A．B．C．D．
【答案】C
【解析】因为，所以.
故选：C
3．（2024·高一·广东广州·期中）欧拉公式（其中为虚数单位，）将指数函数的定义域扩大到复数，建立了三角函数与指数函数的关联，在复变函数论中占有非常重要的地位，被誉为数学中的天桥.依据欧拉公式，则（）
A．B．为实数
C．D．复数对应的点位于第三象限
【答案】C
【解析】对于A选项，，A错；
对于B选项，为纯虚数，B错；
对于C选项，因为，
因此，，C对；
对于D选项，，则，，
所以，复数在复平面内对应的点位于第二象限，D错.
故选：C.
4．（2024·高一·全国·课时练习）如果，那么复数的三角形式是（）
A．
B．
C．
D．
【答案】A
【解析】因为，，
所以.
故选：A.
5．（2024·高一·河北沧州·期中）已知（其中i为虚数单位），那么复数在复平面内所对应的点位于（）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】B
【解析】由，
可得
，
因为，，
所以复数在复平面内所对应的点位于第二象限．
故选：B．
6．（2024·湖北恩施·模拟预测）任意一个复数都可以表示成三角形式，即．棣莫弗定理是由法国数学家棣莫弗（1667－1754年）创立的，指的是：设两个复数，，则，已知复数，则（）
A．B．C．D．1
【答案】B
【解析】由题意可得，
故，
所以
.
故选：B
7．（2024·四川成都·模拟预测）欧拉公式（其中为虚数单位，）是由瑞士著名数学家欧拉创立的，该公式将指数函数的定义域扩大到复数，建立了三角函数与指数函数的关联，在复变函数论里面占有非常重要的地位.依据欧拉公式，下列选项正确的是（）
A．为虚数B．函数不是周期函数
C．若，则D．的共轭复数是
【答案】D
【解析】A选项，，为实数，A错误；
B选项，，由于是最小正周期为的函数，所以是周期函数，B错误；
C选项，由题意得，所以，
又时，，故C错误；
D选项，
，
故共轭复数是，D正确.
故选：D
8．（2024·高一·江苏苏州·期中）欧拉公式是由18世纪瑞士数学家､自然科学家莱昂哈德･欧拉发现的，被誉为数学上优美的公式.已知，则（）
A．B．C．D．
【答案】A
【解析】，
，
，
，，
即，，
.
故选：A.
二、多选题
9．（2024·高一·江西南昌·期末）已知复数（为虚数单位），则下列说法中正确的有（）
A．z的虚部为B．
C．D．
【答案】BD
【解析】对于A，因为，所以z的虚部为，故A错误；
对于B，，故B正确；
对于C，因为一个复数的辐角有无数多个，故错误，故C错误；
对于D，因为，所以，故D正确.
故选：BD.
10．（2024·高一·福建三明·期末）设复数，其中i是虚数单位，下列判断中正确的是（）
A．B．
C．z是方程的一个根D．满足最小正整数n为3
【答案】ACD
【解析】由题设，，则，，
所以A正确，B错误；
由的根为，故z是该方程的一个根，C正确；
由，则，故最小正整数n为3时，，正确.
故选：ACD
11．（2024·高二·福建莆田·开学考试）已知复数，，，为坐标原点，，，对应的向量分别为，，，则以下结论正确的有（）
A．
B．若，则
C．若，则与的夹角为
D．若，则为正三角形
【答案】ABD
【解析】因为，，，
所以，则，
对于A，，
故
，
，
所以，故A正确；
对于B，若，则，故B正确；
对于C，设与的夹角为，
若，则，
即，
即，所以，
所以，即与的夹角为，故C错误；
对于D，若，则，
则，
即，由C选项可知与的夹角为，
同理与的夹角为，与的夹角为，
又，
所以，故D正确.
故选：ABD.
三、填空题
12．（2024·高一·上海浦东新·期末）将复数在复平面上所对应的向量绕原点按顺时针方向旋转得到向量，那么对应的复数是 .
【答案】
【解析】复数的三角形式是,
向量对应的复数是.
故答案为：
13．（2024·高一·全国·课时练习）设复数，则得一个辐角是 .
【答案】（答案不唯一）
【解析】由题意得，
，
所以得辐角是（答案不唯一）
故答案为：（答案不唯一）
14．（2024·高一·上海杨浦·期末）若是纯虚数（其中是虚数单位），则正整数的最小值为 .
【答案】
【解析】因为
因为为纯虚数，则，可得，
可得，又因为，当时，正整数取最小值.
故答案为：.
四、解答题
15．（2024·高一·全国·随堂练习）在复平面内作出下列复数对应的向量，并用三角形式表示（辐角取主值）：
(1)6；
(2)；
(3)；
(4)．
【解析】（1）6对应的向量如答图中，
，又，
.
（2）对应的向量如答图中，
，
又，.
（3）对应的向量如答图中
，
又，.
（4）对应的向量如答图中，
，
又，.
16．（2024·高一·全国·随堂练习）在复平面内，复数，，，它们对应的向量分别为、、，如何直观地理解与、与之间的位置关系呢？
【解析】因为，所以，，
，所以，，
所以，先将沿原方向伸长倍，再逆时针旋转，可得到，
将反向伸长为原来的倍，可得到.
17．（2024·高一·全国·课堂例题）求．
【解析】先将化为三角形式，得，
则原式．
18．（2024·高一·全国·随堂练习）计算：
(1)；
(2)；
(3)；
(4)；
(5)；
(6)．
【解析】（1）.
（2）.
（3）
.
（4）.
（5）.
（6）
.
19．（2024·高一·河北衡水·期末）欧拉是十八世纪数学界最杰出的人物之一，数学史上称十八世纪为“欧拉时代”．1735年，他提出公式：复数：（是虚数单位）．已知复数，，．
(1)当时，求的值；
(2)当时，若且，求的值．
【解析】（1）因为虚数不能比较大小，所以为实数，
又因为，
所以
解得
（2）当时，，．
所以，
所以，
所以，，
因为，所以．
课程标准
学习目标
（1）培养转化，逻辑推理及数学运算能力；
（2）通过对复数的乘、除运算及其几何意义的学习，培养学生直观想象、数学运算、数学建模等数学素养。
（1）掌握复数的三角形式，能够进行两种形式的转化
（2）会进行复数三角形式的乘除运算；
（3）理解复数乘、除运算的三角表示的几何意义.