八年级上册2.2 轴对称的基本性质课文内容ppt课件

这是一份八年级上册2.2 轴对称的基本性质课文内容ppt课件，共18页。PPT课件主要包含了复习回顾，符号语言，∴PAPB，∵PAPB等内容，欢迎下载使用。
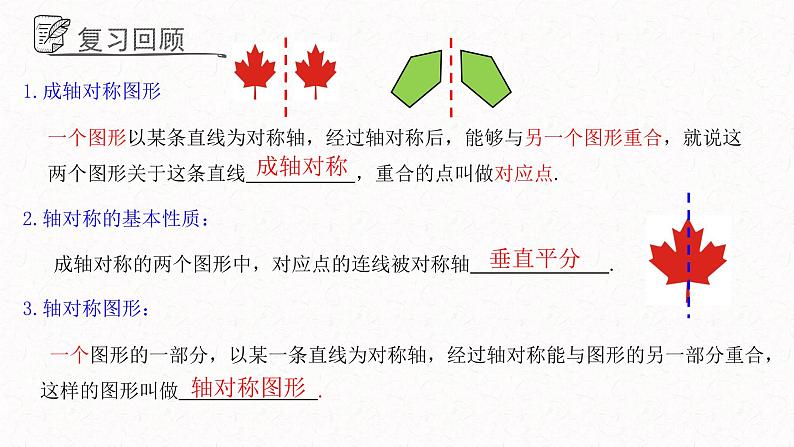
一个图形以某条直线为对称轴，经过轴对称后，能够与另一个图形重合，就说这两个图形关于这条直线 ，重合的点叫做对应点.
2.轴对称的基本性质：
成轴对称的两个图形中，对应点的连线被对称轴 .
一个图形的一部分，以某一条直线为对称轴，经过轴对称能与图形的另一部分重合，这样的图形叫做 .
1.体会线段的轴对称性，认识线段垂直平分线。2.掌握线段垂直平分线的性质并会应用.3.知道到线段两端距离相等的点在线段的垂直平分线上。4.会用尺规作图作出一条线段的垂直平分线。
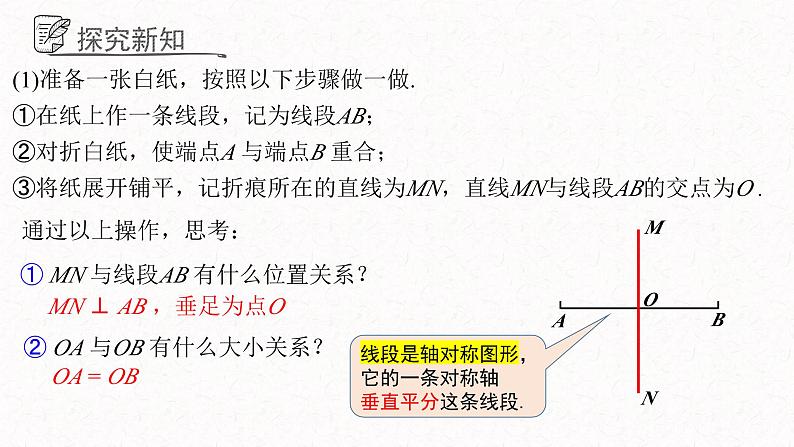
(1)准备一张白纸，按照以下步骤做一做.①在纸上作一条线段，记为线段AB；②对折白纸，使端点A 与端点B 重合；③将纸展开铺平，记折痕所在的直线为MN，直线MN与线段AB的交点为O .
① MN 与线段AB 有什么位置关系？
MN ⊥ AB ，垂足为点O
② OA 与OB 有什么大小关系？
线段是轴对称图形，它的一条对称轴垂直平分这条线段.
垂直并且平分一条线段的直线叫做这条线段的垂直平分线.
线段的垂直平分线是一条直线，且只有一条.
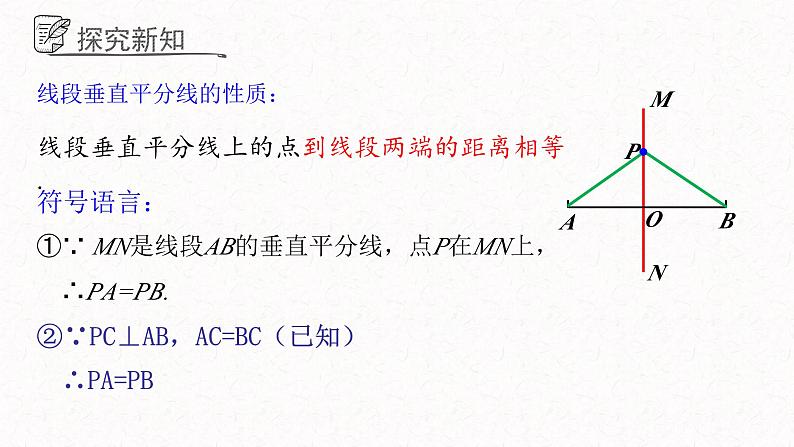
如图，直线MN是线段AB的垂直平分线.
∵直线MN是线段AB的垂直平分线，∴MN⊥AB， OA=OB.或∠AOM =∠BOM=90°，OA=OB.
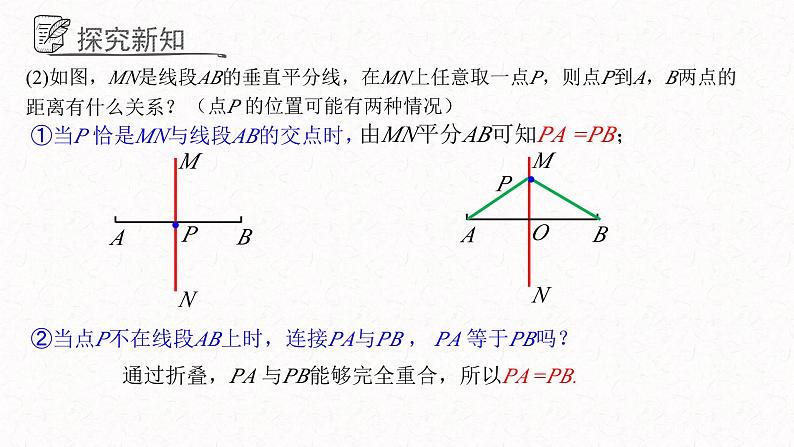
(2)如图，MN是线段AB的垂直平分线，在MN上任意取一点P，则点P到A，B两点的距离有什么关系？
①当P 恰是MN与线段AB的交点时，
②当点P不在线段AB上时，连接PA与PB ， PA 等于PB吗？
由MN平分AB可知PA =PB；
通过折叠，PA 与PB能够完全重合，所以PA =PB.
（点P 的位置可能有两种情况）
线段垂直平分线上的点到线段两端的距离相等.
线段垂直平分线的性质：
①∵ MN是线段AB的垂直平分线，点P在MN上，
②∵PC⊥AB，AC=BC（已知）
1.如图，MN是线段AB的垂直平分线,下列说法正确的有： . ①AB⊥MN ②AD=DB ③MN⊥AB ④MD=DN ⑤AB是MN的垂直平分线
2.如图，已知AB是线段CD的垂直平分线,E是AB上的一点，如果EC=7cm，那么ED= cm
(3)反过来，到线段AB两端距离相等的点是否都在线段的垂直平分线上？
①当P 在线段AB上时，若PA =PB，点P在线段AB的垂直平分线上吗？
∴点P是线段AB的中点，
∴点P在线段AB的垂直平分线上.
②当P不在线段AB上时，若PA =PB，点P在线段AB的垂直平分线上吗？
取线段AB的中点，记为点O，连接PO.
∴△AOP ≌△BOP(SSS),
在△ AOP与△ BOP中，
∴ ∠AOP = ∠ BOP.
∵ ∠AOP +∠ BOP=180°,
即PO是线段AB的垂直平分线.
∴∠AOP = ∠ BOP=90°,
到线段两端距离相等的点在线段的垂直平分线上.
∴ 点P在线段AB的垂直平分线上.
1.如图，AC=AD，BC=BD，则有（　　） A．AB垂直平分CD B．CD垂直平分AB C．AB与CD互相垂直平分 D．CD平分∠ACB
2.如图，P是∠AOB的平分线OM上任意一点，PE⊥CA于E，PF⊥OB于F，连结EF.试说明：OP垂直平分EF.
(4)已知线段AB，你能用尺规作出线段AB的垂直平分线吗？
作图思路：用尺规作一条线段的垂直平分线，只要能作出到这条线段的两个端点距离相等的两个点，这两点所确定的直线就是这条线段的垂直平分线.
直线MN就是线段AB的垂直平分线.
公路l 同侧的A、B两村，共同出资在公路边修建一个农产品仓库C，使仓库到A，B两村距离相等.你如何确定仓库C的位置？
点C就是仓库所在的位置.
3、如图，若AC=12，BC=7，AB的垂直平分线交AB于E，交AC于D，求△BCD的周长。
(一)线段垂直平分线上的点到线段两端的距离相等.
(二)到线段两端距离相等的点在线段的垂直平分线上.