2024年中考数学二轮复习 二次函数压轴题 专项练习十（含答案）

这是一份2024年中考数学二轮复习 二次函数压轴题 专项练习十（含答案），共15页。
如图，抛物线与x轴交于A，B两点(点A在点B的左侧)，与y轴交于点C．
(1)求点A，B，C的坐标及抛物线的对称轴；
(2)如图1，点P(1，m)，Q(1，m﹣2)是两动点，分别连接PC，QB，请求出|PC﹣QB|的最大值，并求出m的值；
(3)如图2，∠BAC的角平分线交y轴于点D，过D点的直线l与射线AB，AC分别于E，F，当直线l绕点D旋转时，是否为定值，若是，请求出该定值；若不是，请说明理由．
如图，在平面直角坐标系中，已知点A坐标为(2，4)，直线x=2与x轴相交于点B，连接OA，抛物线y=x2从点O沿OA方向平移，与直线x=2交于点P，顶点M到A点时停止移动．
(1)求线段OA所在直线的函数解析式；
(2)设抛物线顶点M的横坐标为m，
①用m的代数式表示点P的坐标；
②当m为何值时，线段PB最短；
(3)当线段PB最短时，相应的抛物线上是否存在点Q，使△QMA的面积与△PMA的面积相等？若存在，请求出点Q的坐标；若不存在，请说明理由．
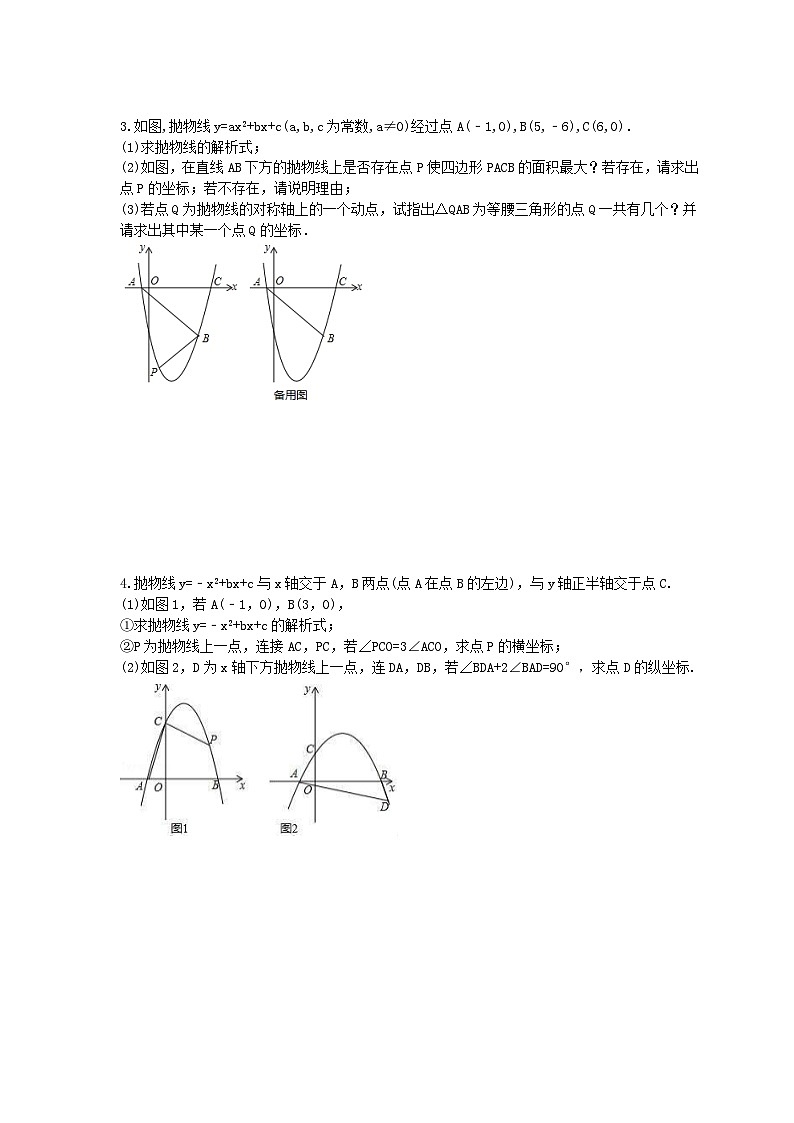
如图,抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0)．
(1)求抛物线的解析式；
(2)如图，在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大？若存在，请求出点P的坐标；若不存在，请说明理由；
(3)若点Q为抛物线的对称轴上的一个动点，试指出△QAB为等腰三角形的点Q一共有几个？并请求出其中某一个点Q的坐标．
抛物线y=﹣x2+bx+c与x轴交于A，B两点(点A在点B的左边)，与y轴正半轴交于点C.
(1)如图1，若A(﹣1，0)，B(3，0)，
①求抛物线y=﹣x2+bx+c的解析式；
②P为抛物线上一点，连接AC，PC，若∠PCO=3∠ACO，求点P的横坐标；
(2)如图2，D为x轴下方抛物线上一点，连DA，DB，若∠BDA+2∠BAD=90°，求点D的纵坐标.
如图，在直角坐标系中，已知点A(0，2)，点B(﹣2，0)，过点B和线段OA的中点C作直线BC，以线段BC为边向上作正方形BCDE．
(1)填空：点D的坐标为( )，点E的坐标为( )；
(2)若抛物线y=﹣eq \f(1,2)x2＋bx＋c经过A，D，E三点，求该抛物线的表达式；
(3)若正方形和抛物线均以每秒eq \r(5)个单位长度的速度沿射线BC同时向上平移，直至正方形的顶点E落在y轴上时，正方形和抛物线均停止运动．
①在运动过程中，设正方形落在y轴右侧部分的面积为S，求S关于平移时间t(1≤t≤eq \f(3,2))的函数关系式；
②运动停止时，求抛物线的顶点坐标．
如图，在平面直角坐标系中，矩形ABCD的边AB在x轴上，且AB=3，BC=2eq \r(3)，
直线y=eq \r(3)x-2eq \r(3)经过点C，交y轴于点G．
(1)点C、D的坐标；
(2)求顶点在直线y=eq \r(3)x-2eq \r(3)上且经过点C、D的抛物线的解析式；
(3)将(2)中的抛物线沿直线y=eq \r(3)x-2eq \r(3)平移，平移后的抛物线交y轴于点F，顶点为点E．
平移后是否存在这样的抛物线，使△EFG为等腰三角形？若存在，请求出此时抛物线的解析式；若不存在，请明理由．
抛物线：y＝﹣x2＋bx＋c与y轴的交点C(0，3)，与x轴的交点分别为E、G两点，对称轴方程为x＝1．
(1)求抛物线的解析式；
(2)如图1，过点C作y轴的垂线交抛物线于另一点D，F为抛物线的对称轴与x轴的交点，P为线段OC上一动点．若PD⊥PF，求点P的坐标．
(3)如图1，如果一个圆经过点O、点G、点C三点，并交于抛物线对称轴右侧x轴的上方于点H，求∠OHG的度数；
(4)如图2，将抛物线向下平移2个单位长度得到新抛物线L，点B是顶点．直线y＝kx﹣k＋4(k＜0)与抛物线L交于点M、N．与对称轴交于点G，若△BMN的面积等于2eq \r(2)，求k的值．
如图1，已知抛物线经过原点O和x轴上一点A(4，0)，抛物线顶点为E，它的对称轴与x轴交于点D，直线y＝﹣2x﹣1经过抛物线上一点B(﹣2，m)且与y轴交于点C，与抛物线的对称轴交于点F．
(1)求m的值及该抛物线的解析式；
(2)P(x，y)是抛物线上的一点，若△ADP与△ADC的面积相等，求出所有符合条件的点P的坐标．
(3)点Q是平面内任意一点，点M从点F出发，沿对称轴向上以每秒1个单位长度的速度匀速运动，设点M的运动时间为t秒，是否能使以Q、A、E、M四点为顶点的四边形是菱形？若能，请直接写出点M的运动时间t的值；若不能，请说明理由．
\s 0 答案
解：(1)当x＝0时，y＝﹣4，
∴C(0，﹣4)，
当y＝0时， x2﹣﹣4＝0，
∴x1＝﹣3，x2＝5，
∴A(﹣3，0)，B(5，0)；
∵＝1，
∴抛物线的对称轴为直线x＝1；
(1)如图1，将点B向上平移2个单位至B′(5，2)，作点C关于直线x＝1的对称点C′(2，﹣4)，作直线B′C′交直线x＝1于点P′，则|PC﹣BQ|最大值是：B′C′的长，
∵B′C′＝3eq \r(5)，∴|PC﹣BQ|最大＝3eq \r(5)，
∵直线B′C′的解析式为：y＝2x﹣8，
∴当x＝1时，y＝2×1﹣8＝﹣6，
∴m＝﹣6；
(3)为定值，理由如下：如图2，
作DG⊥AC于G，作FH⊥AB于H，∵AD平分∠BAC，
∴OD＝DG，
∵S△AOC＝S△AOD＋S△ACD，
∴OD＝eq \f(3,2)，∵D(0，﹣eq \f(3,2))，
∴设直线EF的关系式为：y＝kx﹣eq \f(3,2)，
∴E(，0)，
∵FH∥OC，OD∥FH，
∴△AHF∽△AOC，△DOE∽△FHE，
∴＝＝，＝＝＝，
设AH＝3a，FH＝4a，
∴＝，∴EH＝，
∵AH＋EH＝AE，
∴3a＋＝，∴a＝，∴AF＝5a＝
∴＋＝＋＝
解：(1)设OA所在直线的函数解析式为y=kx，
∵A(2，4)，∴2k=4，∴k=2，
∴OA所在直线的函数解析式为y=2x．
(2)①∵顶点M的横坐标为m，且在线段OA上移动，
∴y=2m(0≤m≤2)．∴顶点M的坐标为(m，2m)．
∴抛物线函数解析式为y=(x﹣m)2+2m．
∴当x=2时，y=(2﹣m)2+2m=m2﹣2m+4(0≤m≤2)．
∴点P的坐标是(2，m2﹣2m+4)．
②∵PB=m2﹣2m+4=(m﹣1)2+3，
又∵0≤m≤2，∴当m=1时，PB最短．
(3)当线段PB最短时，此时抛物线的解析式为y=(x﹣1)2+2
即y=x2﹣2x+3．
假设在抛物线上存在点Q，使S△QMA=S△PMA．
设点Q的坐标为(x，x2﹣2x+3)．
①点Q落在直线OA的下方时，过P作直线PC∥AO，交y轴于点C，
∵PB=3，AB=4，∴AP=1，∴OC=1，∴C点的坐标是(0，﹣1)．
∵点P的坐标是(2，3)，∴直线PC的函数解析式为y=2x﹣1．
∵S△QMA=S△PMA，∴点Q落在直线y=2x﹣1上．
∴x2﹣2x+3=2x﹣1．解得x1=2，x2=2，即点Q(2，3)．
∴点Q与点P重合．
∴此时抛物线上不存在点Q(2，3)，使△QMA与△APM的面积相等．
②当点Q落在直线OA的上方时，
作点P关于点A的对称称点D，过D作直线DE∥AO，交y轴于点E，
∵AP=1，∴EO=DA=1，∴E、D的坐标分别是(0，1)，(2，5)，
∴直线DE函数解析式为y=2x+1．
∵S△QMA=S△PMA，∴点Q落在直线y=2x+1上．
∴x2﹣2x+3=2x+1．解得：x1=2+eq \r(2)，x2=2﹣eq \r(2)．
代入y=2x+1得：y1=5+2eq \r(2)，y2=5﹣2eq \r(2)．
∴此时抛物线上存在点Q1(2+eq \r(2)，5+2eq \r(2))，Q2(2﹣eq \r(2)，5﹣2eq \r(2))
使△QMA与△PMA的面积相等．
综上所述，抛物线上存在点，Q1(2+eq \r(2)，5+2eq \r(2))，Q2(2﹣eq \r(2)，5﹣2eq \r(2))
使△QMA与△PMA的面积相等．
解：(1)设y=a(x+1)(x﹣6)(a≠0)，
把B(5，﹣6)代入：a(5+1)(5﹣6)=﹣6，a=1，
∴y=(x+1)(x﹣6)=x2﹣5x﹣6；
(2)存在，如图1，分别过P、B向x轴作垂线PM和BN，垂足分别为M、N，
设P(m，m2﹣5m﹣6)，四边形PACB的面积为S，
则PM=﹣m2+5m+6，AM=m+1，MN=5﹣m，CN=6﹣5=1，BN=5，
∴S=S△AMP+S梯形PMNB+S△BNC
=eq \f(1,2)(﹣m2+5m+6)(m+1)+eq \f(1,2)(6﹣m2+5m+6)(5﹣m)+eq \f(1,2)×1×6
=﹣3m2+12m+36=﹣3(m﹣2)2+48，
当m=2时，S有最大值为48，这时m2﹣5m﹣6=22﹣5×2﹣6=﹣12，
∴P(2，﹣12)，
(3)这样的Q点一共有5个，连接Q3A、Q3B，
y=x2﹣5x﹣6=(x﹣eq \f(5,2))2﹣12eq \f(1,4)；
因为Q3在对称轴上，所以设Q3(eq \f(5,2)，y)，
∵△Q3AB是等腰三角形，且Q3A=Q3B，
由勾股定理得：(eq \f(5,2)+1)2+y2=(eq \f(5,2)﹣5)2+(y+6)2，y=﹣eq \f(5,2)，∴Q3(，﹣eq \f(5,2))．
解：(1)①将A(﹣1，0)、B(3，0)代入y=﹣x2+bx+c，得：
，解得：，
∴y=﹣x2+2x+3；
②延长CP交x轴于点E，在x轴上取点D，使CD=CA，作EN⊥CD交CD的延长线于点N，
∵CD=CA、OC⊥AD，
∴∠DCO=∠ACO，
∵∠PCO=3∠ACO，
∴∠ACD=∠ECD，
∴tan∠ACD=tan∠ECD，
∴=，AI==，
∴CI==，
∴==，
设EN=3x，则CN=4x，
由tan∠CDO=tan∠EDN知==，
∴DN=x，
∴CD=CN﹣DN=3x=eq \r(10)，
∴x=，∴DE=，则点E的坐标为(，0)，
所以直线CE的解析式为y=﹣x+3，
由可得x1=0、x2=，则点P的横坐标为.
(2)如图2，作DI⊥x轴，垂足为I，
∵∠BDA+2∠BAD=90°，
∴∠DBI+∠BAD=90°，
∵∠BDI+∠DBI=90°，
∴∠BAD=∠BDI，
∵∠BID=∠DIA，
∴△IBD∽△IDA，
∴=，∴=，
∴yD2=xD2﹣(xA+xB)xD+xAxB，
令y=0，得：﹣x2+bx+c=0，则xA+xB=b、xAxB=﹣c，
∴yD2=xD2﹣(xA+xB)xD+xAxB=xD2﹣bxD﹣c，
∵yD=﹣xD2+bxD+c，
∴yD2=﹣yD，解得：yD=0或﹣1，
∵点D在x轴下方，
∴yD=﹣1，即点D的纵坐标为﹣1.
解：(1)由题意可知：OB=2，OC=1．
如图(1)所示，过D点作DH⊥y轴于H，过E点作EG⊥x轴于G．
易证△CDH≌△BCO，∴DH=OC=1，CH=OB=2，∴D(﹣1，3)；
同理△EBG≌△BCO，∴BG=OC=1，EG=OB=2，∴E(﹣3，2)．
∴D(﹣1，3)、E(﹣3，2)，故答案为：(﹣1，3)(﹣3，2)；
(2)抛物线经过(0，2)、(﹣1，3)、(﹣3，2)，
则解得，
∴y=﹣eq \f(1,2)x2﹣eq \f(3,2)x＋2；
(3)①当点D运动到y轴上时，t=eq \f(1,2)．当0＜t≤eq \f(1,2)时，
如图(3)a所示．设D′C′交y轴于点F
∵tan∠BCO==2，
又∵∠BCO=∠FCC′∴tan∠FCC′=2，即=2
∵CC′=eq \r(5)t，∴FC′=2eq \r(5)t．
∴S△CC′F=eq \f(1,2)CC′•FC′=eq \f(1,2)t×2eq \r(5)t=5t2
当点B运动到点C时，t=1．
当eq \f(1,2)＜t≤1时，如图(3)b所示．
设D′E′交y轴于点G，过G作GH⊥B′C′于H．
在Rt△BOC中，BC=eq \r(5)，∴GH=eq \r(5)，∴CH=eq \f(1,2)GH=eq \f(\r(5),2)，
∵CC′=eq \r(5)t，∴HC′=eq \r(5)t﹣eq \f(\r(5),2)，∴GD′=eq \r(5)t﹣eq \f(\r(5),2)，
∴S梯形CC′D′G=eq \f(1,2)(eq \r(5)t﹣eq \f(\r(5),2)＋eq \r(5)t)=5t﹣eq \f(5,4)，
当点E运动到y轴上时，t=eq \f(3,2)．
当1＜t≤15时，如图(3)c所示,设D′E′、E′B′分别交y轴于点M、N，
∵CC′=eq \r(5)t，B′C′=eq \r(5)，∴CB′=eq \r(5)t﹣eq \r(5)，∴B′N=2CB′=2eq \r(5)t﹣2eq \r(5)，
∵B′E′=eq \r(5)，∴E′N=B′E′﹣B′N=3eq \r(5)﹣2eq \r(5)t
∴E′M=eq \f(1,2)E′N=eq \f(1,2)(3eq \r(5)﹣2eq \r(5)t)，
∴S△MNE=eq \f(1,2)(3eq \r(5)﹣2eq \r(5)t)•eq \f(1,2)(3eq \r(5)﹣2eq \r(5)t)=5t2﹣15t＋11eq \f(1,4)，
∴S五边形B′C′D′MN=S正方形B′C′D′E′﹣S△MNE′=2eq \r(5)(5t2﹣15t＋11eq \f(1,4))=﹣5t2＋15t﹣11eq \f(1,4)，
综上所述，S与x的函数关系式为：当0＜t≤0.5时，S=5t2
当0.5＜t≤1时，S=5t﹣eq \f(5,4)，当1＜t≤eq \f(3,2)时，S=﹣5t2＋15t﹣11eq \f(1,4)，
②当点E运动到点E′时，运动停止．如图(3)d所示：
∵∠CB′E′=∠BOC=90°，∠BCO=∠B′CE′，
∴△BOC∽△E′B′C，∴=，
∵OB=2，B′E′=BC=eq \r(5)，∴，∴CE′=eq \f(5,2)，
∴OE′=OC＋CE′=1＋eq \f(5,2)=eq \f(7,2)，∴E′(0，eq \f(7,2))，
由点E(﹣3，2)运动到点E′(0，eq \f(7,2))，
可知整条抛物线向右平移了3个单位，向上平移了eq \f(3,2)个单位．
∵y=﹣eq \f(1,2)x2﹣eq \f(3,2)x＋2=﹣eq \f(1,2)(x＋eq \f(3,2))2＋3eq \f(1,8)，∴原抛物线顶点坐标为(﹣eq \f(3,2)，3eq \f(1,8))，
∴运动停止时，抛物线的顶点坐标为(eq \f(3,2)，4eq \f(5,8))．
解：(1)令y=2eq \r(3)，2eq \r(3)=y=eq \r(3)x-2eq \r(3)，解得x=4，则OA=4﹣3=1，
∴C(4，2eq \r(3))，D(1，2eq \r(3))；
(2)由二次函数对称性得，顶点横坐标为=2.5，
令x=eq \f(5,2)，则y=eq \r(3)×eq \f(5,2)﹣2eq \r(3)=eq \f(\r(3),2)，∴顶点坐标为(eq \f(5,2)，eq \f(\r(3),2))，
∴设抛物线解析式为y=a(x﹣eq \f(5,2))2﹣eq \f(\r(3),2)，把点D(1，2eq \r(3))代入得，a=eq \f(2\r(3),3)，
∴解析式为y=eq \f(2\r(3),3)(x﹣eq \f(5,2))2﹣eq \f(\r(3),2)；
(3)设顶点E在直线上运动的横坐标为m，则E(m，eq \r(3)m﹣2eq \r(3))(m＞0)
∴可设解析式为y=eq \f(2\r(3),3)(x﹣m)2﹣eq \r(3)m﹣2eq \r(3)，
①当FG=EG时，FG=EG=2m，则F(0，2m﹣2eq \r(3))，
代入解析式得：eq \f(2\r(3),3)m2﹣eq \r(3)m﹣2eq \r(3)=2m﹣2eq \r(3)，
得m=0(舍去)，m=eq \r(3)﹣eq \f(3,2)，
此时所求的解析式为：y=eq \f(2\r(3),3)(x﹣eq \r(3)﹣eq \f(3,2))2﹣3﹣eq \f(7,2)eq \r(3)；
②当GE=EF时，FG=2eq \r(3)m，则F(0，2eq \r(3)m﹣2eq \r(3))，
代入解析式得：eq \f(2\r(3),3)m2﹣eq \r(3)m﹣2eq \r(3)=2eq \r(3)m﹣2eq \r(3)，解得m=0(舍去)，m=eq \f(3,2)，
此时所求的解析式为：y=eq \f(2\r(3),3)(x﹣eq \f(3,2))2﹣eq \f(\r(3),2)；
③当FG=FE时，不存在．
解：(1)将C(0，3)代入y＝﹣x2＋bx＋c可得c＝3，
∵对称轴是直线x＝1，
∴x＝1，解得b＝2，
∴二次函数解析式为y＝﹣x2＋2x＋3；
(2)∵y＝﹣x2＋2x＋3与y轴的交点C(0，3)，对称轴方程为x＝1．CD⊥y轴，
∴D(2，3)，
∵对称轴与x轴相较于点F，
∴点F的坐标为(1，0)，
设P点坐标为(0，a)，
∵CD⊥y轴，OF⊥y轴，
∴∠DCF＝∠POF＝90°
∴∠OFP＋∠OPF＝90°，
∵PD⊥PF，
∴∠DPF＝90°，
∴∠CPD＋∠OPF＝90°，
∴∠OFP＝∠CPD，
∴△CDP∽△OPF，
∴，∴，解得：a1＝1，a2＝2，
∴P点的坐标为(0，1)或(0，2)；
(3)如图：连接CG，
∵y＝﹣x2＋2x＋3，
令y＝0，则﹣x2＋2x＋3＝0，解得x＝3或x＝﹣1，
∴G(3，0)，E(﹣1，0)，
∴OG＝OC，
∵OC⊥OG，
∴△COG为等腰直角三角形，
∴∠OCG＝45°，
∵点O、点G、点C、点H四点共圆，
∴∠OHG＝∠OCG＝45°；
(4)∵将抛物线向下平移2个单位长度得到抛物线L，
∴抛物线L的解析式为y＝﹣x2＋2x＋3﹣2＝﹣x2＋2x＋1＝﹣(x﹣1)2＋2，
∴B点坐标为(1，2)，联立，即kx﹣k＋4＝﹣x2＋2x＋1，
∴x2＋(k﹣2)x＋3﹣k＝0，设两个交点为N(x1，y1)，M(x2，y2)，
则x1＋x2＝2﹣k，x1x2＝3﹣k，
S△BMN＝S△BGN﹣S△BGM＝＝BG
＝＝BG＝2，
把x＝1代入y＝kx﹣k＋4，得；y＝4，
∴G(1，4)，
∵B(1，2)，
∴BG＝4﹣2＝2，
∴，解得：k＝±4，
∵k＜0，
∴k＝﹣4．
解：(1)∵点B(﹣2，m)在直线y＝﹣2x﹣1上，
∴m＝﹣2×(﹣2)﹣1＝4﹣1＝3，
∴点B(﹣2，3)，
又∵抛物线经过原点O，
∴设抛物线的解析式为y＝ax2＋bx，
∵点B(﹣2，3)，A(4，0)在抛物线上，
∴，解得．
∴抛物线的解析式为y=eq \f(1,4)x2-x；
(2)如图1，∵P(x，y)是抛物线上的一点，
∴P(x,eq \f(1,4)x2-x)，
若S△ADP＝S△ADC，
∵S△ADC＝eq \f(1,2)AD•OC，S△ADP＝eq \f(1,2)AD|y|，
又∵点C是直线y＝﹣2x﹣1与y轴交点，
∴C(0，﹣1)，
∴OC＝1，
∴|eq \f(1,4)x2﹣x|＝1，即eq \f(1,4)x 2﹣x＝1，或eq \f(1,4)x2﹣x＝﹣1，
解得：x1＝2＋2eq \r(2)，x2＝2﹣2eq \r(2)，x3＝x4＝2，
∴点P的坐标为 P1(2＋2eq \r(2)，1)，P2(2﹣2eq \r(2)，1)，P3 (2，1)；
(3)结论：存在．
∵抛物线的解析式为y＝eq \f(1,4)x2﹣x，
∴顶点E(2，﹣1)，对称轴为x＝2；
点F是直线y＝﹣2x﹣1与对称轴x＝2的交点，
∴F(2，﹣5)，DF＝5．
又∵A(4，0)，
∴AE＝eq \r(5)．
如图2，在点M的运动过程中，依次出现四个菱形：
①四边形AEM1Q1是菱形．
∵此时EM1＝AE＝eq \r(5)，
∴M1F＝DF﹣DE﹣DM1＝4﹣eq \r(5)，
∴t1＝4﹣eq \r(5)；
②四边形AEOM2是菱形．
∵此时DM2＝DE＝1，
∴M2F＝DF＋DM2＝6，
∴t2＝6；
③四边形AEM3Q3是菱形．
∵此时EM3＝AE＝eq \r(5)，
∴DM3＝EM3﹣DE＝eq \r(5)﹣1，
∴M3F＝DM3＋DF＝(eq \r(5)﹣1)＋5＝4＋eq \r(5)，
∴t3＝4＋eq \r(5)；
④四边形AM4EQ4是菱形．
此时AE为菱形的对角线，设对角线AE与M4Q4交于点H，则AE⊥M4Q4，
∵∠ADE＝∠M4HD＝90°，∠AED＝∠M4DH，
∴△AED∽△M4EH，
∴，解得，
∴DM4＝M4E﹣DE＝eq \f(3,2)，
∴M4F＝DM4＋DF＝eq \f(3,2)＋5＝eq \f(13,2)，
∴t4＝eq \f(13,2)．
综上所述，存在点M、点Q，使得以Q、A、E、M四点为顶点的四边形是菱形；时间t的值为：t1＝4﹣eq \r(5)，t2＝6，t3＝4＋eq \r(5)，t4＝eq \f(13,2)．