2024年中考数学二轮复习 二次函数压轴题 专项练习二（含答案）

这是一份2024年中考数学二轮复习 二次函数压轴题 专项练习二（含答案），共16页。
如图，二次函数y=x2+bx+c的图象交x轴于A(﹣1，0)、B(3，0)两点，交y轴于点C，连接BC，动点P以每秒1个单位长度的速度从A向B运动，动点Q以每秒个单位长度的速度从B向C运动，P、Q同时出发，连接PQ，当点Q到达C点时，P、Q同时停止运动，设运动时间为t秒．
(1)求二次函数的解析式；
(2)如图1，当△BPQ为直角三角形时，求t的值；
(3)如图2，当t＜2时，延长QP交y轴于点M，在抛物线上是否存在一点N，使得PQ的中点恰为MN的中点？若存在，求出点N的坐标与t的值；若不存在，请说明理由．
如图，已知直线y＝﹣eq \f(1,2)x＋1与坐标轴交于A，B两点，以线段AB为边向上作正方形ABCD，过点A，D，C的抛物线与直线的另一个交点为E．
(1)求抛物线的解析式；
(2)若正方形以每秒eq \r(5)个单位长度的速度沿射线AB下滑，直至顶点D落在x轴上时停止，设正方形落在x轴下方部分的面积为S，求S关于滑行时间t的函数关系式，并写出相应自变量t的取值范围；
(3)在(2)的条件下，抛物线与正方形一起平移，同时停止，求抛物线上C，E两点间的抛物线弧所扫过的面积．
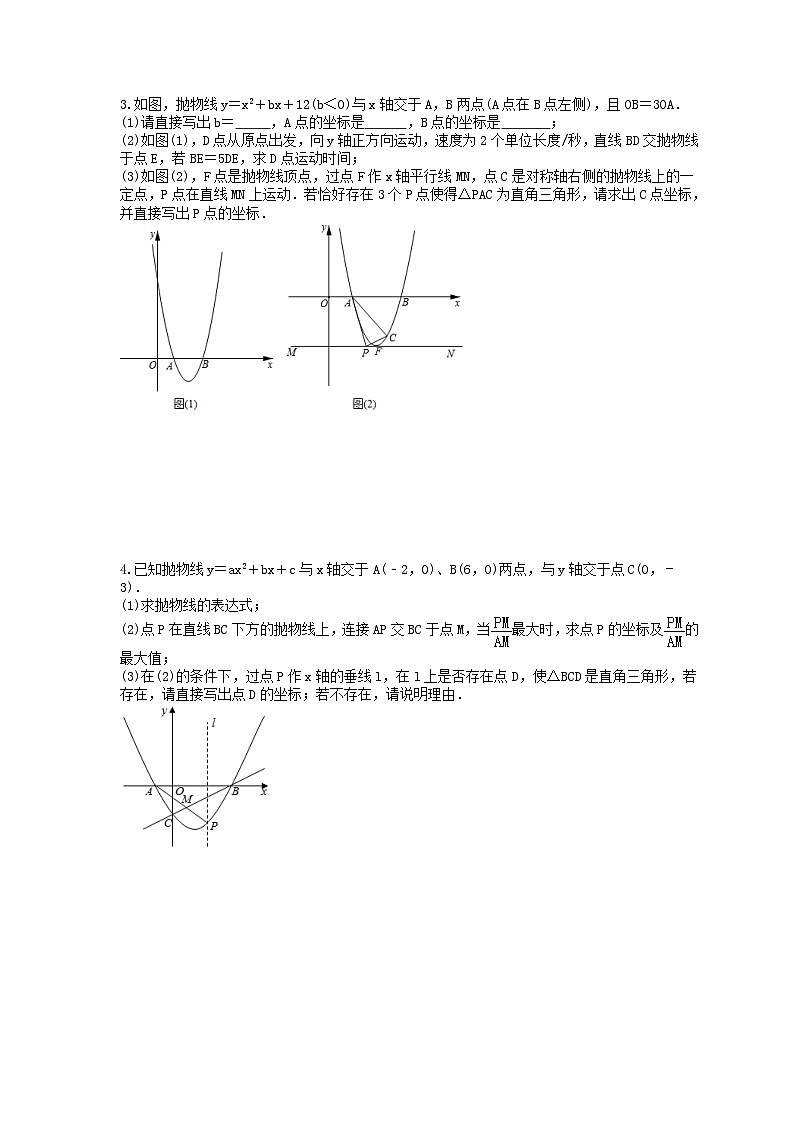
如图，抛物线y＝x2＋bx＋12(b＜0)与x轴交于A，B两点(A点在B点左侧)，且OB＝3OA．
(1)请直接写出b＝ ，A点的坐标是 ，B点的坐标是 ；
(2)如图(1)，D点从原点出发，向y轴正方向运动，速度为2个单位长度/秒，直线BD交抛物线于点E，若BE＝5DE，求D点运动时间；
(3)如图(2)，F点是抛物线顶点，过点F作x轴平行线MN，点C是对称轴右侧的抛物线上的一定点，P点在直线MN上运动．若恰好存在3个P点使得△PAC为直角三角形，请求出C点坐标，并直接写出P点的坐标．
已知抛物线y＝ax2＋bx＋c与x轴交于A(﹣2，0)、B(6，0)两点，与y轴交于点C(0，﹣3)．
(1)求抛物线的表达式；
(2)点P在直线BC下方的抛物线上，连接AP交BC于点M，当最大时，求点P的坐标及的最大值；
(3)在(2)的条件下，过点P作x轴的垂线l，在l上是否存在点D，使△BCD是直角三角形，若存在，请直接写出点D的坐标；若不存在，请说明理由．
如图，已知抛物线y＝eq \f(1,a)(x﹣2)(x＋a)(a＞0)与x轴交于点B、C，与y轴交于点E，且点B在点C的左侧．
(1)若抛物线过点M(﹣2，﹣2)，求实数a的值；
(2)在(1)的条件下，解答下列问题；
①求出△BCE的面积；
②在抛物线的对称轴上找一点H，使CH＋EH的值最小，直接写出点H的坐标．
抛物线y＝ax2＋bx＋3(a≠0)经过点A(﹣1，0)，B(eq \f(3,2)，0)，且与y轴相交于点C.
(1)求这条抛物线的表达式；
(2)求∠ACB的度数；
(3)设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标.
在平面直角坐标系中，点O为坐标系的原点，经过点B(3，6)的抛物线y=-eq \f(1,2)x2+bx与x轴的正半轴交于点A．
(1)求抛物线的解析式；
(2)如图1，点P为第一象限抛物线上的一点，且点P在抛物线对称轴的右侧，连接OP，AP，设点P的横坐标为t，△OPA的面积为S，求S与t的函数解析式(不要求写出自变量t的取值范围)；
(3)如图2，在(2)的条件下，当S=17.5时，连接BP，点C为线段OA上的一点，过点C作x轴的垂线交BP的延长线于点D，连接OD，BC，若∠ODB-eq \f(1,2)∠CBD=∠AOP，求点C的坐标．
把Rt△ABC和Rt△DEF按如图(1)摆放(点C与E重合)，点B、C(E)、F在同一条直线上．已知：∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=10cm．如图(2)，△DEF从图(1)的位置出发，以1cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点A出发，以2cm/s的速度沿AB向点B匀速移动；当点P移动到点B时，点P停止移动，△DEF也随之停止移动．DE与AC交于点Q，连接PQ，设移动时间为t(s)．
(1)用含t的代数式表示线段AP和AQ的长，并写出t的取值范围；
(2)连接PE，设四边形APEQ的面积为y(cm2)，试探究y的最大值；
(3)当t为何值时，△APQ是等腰三角形．

\s 0 答案
解：(1)∵二次函数y=x2+bx+c的图象经过A(﹣1，0)、B(3，0)两点，
∴，解得．
∴二次函数的解析式是：y=x2﹣2x﹣3．
(2)∵y=x2﹣2x﹣3，∴点C的坐标是(0，﹣3)，∴BC=3eq \r(2)，
设BC所在的直线的解析式是：y=mx+n，
则，解得．
∴BC所在的直线的解析式是：y=x﹣3，
∵经过t秒，AP=t，BQ=eq \r(2)t，∴点P的坐标是(t﹣1，0)，
设点Q的坐标是(x，y)，
∵OB=OC=3，∴∠OBC=∠OCB=45°，则y=eq \r(2)t×sin45°=t，
∴BP=eq \r(2)t×eq \f(\r(2),2)=t，∴x=3﹣t，
∴点Q的坐标是(3﹣t，t)，
①如图1，当∠QPB=90°时，点P和点Q的横坐标相同，
∵点P的坐标是(t﹣1，0)，点Q的坐标是(3﹣t，t)，∴t﹣1=3﹣t，解得t=2，
即当t=2时，△BPQ为直角三角形．
②如图2，当∠PQB=90°时，∵∠PBQ=45°，∴BP=eq \r(2)BQ，
∵BP=3﹣(t﹣1)=4﹣t，BQ=eq \r(2)t，
∴4﹣t=eq \r(2)×eq \r(2)t即4﹣t=2t，解得t=eq \f(4,3)，即当t=eq \f(4,3)时，△BPQ为直角三角形．
综上，可得当△BPQ为直角三角形，t=eq \f(4,3)或2．
(3)如图3，延长MQ交抛物线于点N，H是PQ的中点，设PQ所在的直线的解析式是y=cx+d，
∵点P的坐标是(t﹣1，0)，点Q的坐标是(3﹣t，t)，
∴，解得．
∴PQ所在的直线的解析式是y=x+，∴点M的坐标是(0，)
∵，，
∴PQ的中点H的坐标是(1，)假设PQ的中点恰为MN的中点，
∵1×2﹣0=2，=，∴点N的坐标是(2，)，
又∵点N在抛物线上，∴=22﹣2×2﹣3=﹣3，解得t=或t=﹣(舍去)，
∵＞，
∴当t＜2时，延长QP交y轴于点M，在抛物线上不存在一点N，使得PQ的中点恰为MN的中点．
解：(1)∵直线y＝﹣eq \f(1,2)x＋1，
∴当x＝0时，y＝1，当y＝0时，x＝2，
∴OA＝1，OB＝2，
过C作CZ⊥x轴于Z，过D作DM⊥y轴于M，
∵四边形ABCD是正方形，
∴AD＝AB＝BC，∠ABC＝∠AOB＝∠CZB＝90°，
∴∠ABO＋∠CBZ＝90°，∠OAB＋∠ABO＝90°，
∴∠OAB＝∠CBZ，
在△AOB和△BZC中，
，
∴△AOB≌△BZC(AAS)，
∴OA＝BZ＝1，OB＝CZ＝2，
∴C(3，2)，
同理可求D的坐标是(1，3)；
设抛物线为y＝ax2＋bx＋c，
∵抛物线过A(0，1)，D(1，3)，C(3，2)，
则，解得，
∴抛物线的解析式为y＝﹣x2＋x＋1；
(2)∵OA＝1，OB＝2，
∴由勾股定理得：AB＝eq \r(5)，
①当点A运动到x轴上点F时，t＝1，
当0＜t≤1时，如图1，
∵∠OFA＝∠GFB′，tan∠OFA＝，
∴tan∠GFB′＝＝＝，∴GB′＝t，
∴S△FB′G＝eq \f(1,2)FB′×GB′＝eq \f(5,4)t2；
②当点C运动x轴上时，t＝2，当1＜t≤2时，如图2，
∵AB＝A′B′＝eq \r(5)，
∴A′F＝eq \r(5)t﹣eq \r(5)，
∴A′G＝eq \f(\r(5),2)(t﹣1)，
∵B′H＝eq \f(\r(5),2)t，
∴S四边形A′B′HG＝eq \f(1,2)(A′G＋B′H)A′B′＝eq \f(5,2)t﹣eq \f(5,4)；
③当点D运动到x轴上时，t＝3，当2＜t≤3时，如图3，
∵A′G＝eq \f(\r(5),2)(t﹣1)，
∴GD′＝eq \f(3,2)eq \r(5)﹣eq \f(\r(5),2)t，
∵S△AOF＝eq \f(1,2)×2×1＝1，OA＝1，∠AOF＝∠GD′H＝90°，∠AFO＝∠GFA′，
∴△AOF∽△GA′F，
∴＝()2，∴S△GA′F＝()2，
则S五边形GA′B′CH＝﹣eq \f(5,4)t2＋eq \f(15,2)t﹣eq \f(25,4)；
综上，S＝；
(3)设平移后点E和点C对应的点为E′、C′，
则抛物线上C，E两点间的抛物线弧所扫过的面积即为▱EE′C′C的面积，
联立y＝﹣eq \f(1,2)x＋1与y＝﹣x2＋x＋1并解得，
∴E(4，﹣1)，
∴BC＝BE，CE＝eq \r(10)，
当顶点D落在x轴上时，抛物线向下平移了3个单位长度，向右平移了6个单位长度，此时点E′的坐标为(10，﹣4)，
∴EE′＝3eq \r(5)，
∴抛物线上C，E两点间的抛物线弧所扫过的面积为S＝EE′BC＝3eq \r(5)×eq \r(5)＝15．
解：(1)根据题意，设A(m，0)，B(3m，0)，
∴y＝(x﹣m)(x﹣3m)＝x2﹣4mx＋3m2，
∴3m2＝12，
解得：m＝±2，
∵m＞0，
∴m＝2，3m＝6，
∴b＝﹣4m＝﹣8，A(2，0)，B(6，0)，
故答案为：﹣8，(2，0)，(6，0)；
(2)由(1)知，抛物线解析式为y＝x2﹣8x＋12，OB＝6，
令x＝0，得y＝12，
∴C(0，12)，
∴OC＝12，
设D点运动时间为t秒，则OD＝2t，
①当t≤6时，点D在线段OC上，如图(1)，过点E作EK∥x轴交y轴于点K，
∵EK∥OB，
∴＝＝，
∵BE＝5DE，
∴BD＝DE＋BE＝6DE，
∴＝＝，
∴OD＝6DK，EK＝1，
∴DK＝eq \f(1,3)t，
∴OK＝OD﹣DK＝2t﹣eq \f(1,3)t＝eq \f(5,3)t，
∴E(1，eq \f(5,3)t)，
∴eq \f(5,3)t＝12﹣8×1＋12，
∴t＝3，
②当t＞6时，点D在线段OC的延长线上，如图(1′)，
过点E作EK∥OB交y轴于点K，
∵BE＝5DE，
∴BD＝BE﹣DE＝4DE，
∵EK∥OB，
∴＝＝，即＝＝＝，
∴EK＝eq \f(3,2)，DK＝eq \f(1,2)t，
∴OK＝OD＋DK＝2t＋eq \f(1,2)t＝eq \f(5,2)t，
∴E(﹣eq \f(3,2)，eq \f(5,2)t)，
∴eq \f(5,2)t＝(﹣eq \f(3,2))2﹣8×(﹣eq \f(3,2))＋12，解得：t＝eq \f(21,2)，
综上所述，D点运动时间为3秒或eq \f(21,2)秒；
(3)∵y＝x2﹣8x＋12＝(x﹣4)2﹣4，
∴顶点F(4，﹣4)，
∵MN∥x轴且经过点F(4，﹣4)，
∴直线MN为y＝﹣4，
∵P点在直线MN上运动，
∴设P(t，﹣4)，
∵△PAC为直角三角形，
∴∠APC＝90°或∠PAC＝90°或∠ACP＝90°，
①当∠APC＝90°时，设点C(m，n)，如图(2)，
过点A作AG⊥MN，过点C作CH⊥MN，
∴∠AGP＝∠CHP＝∠APC＝90°，
AG＝4，CH＝n＋4，PH＝m﹣t，PG＝t﹣2，
∴∠GAP＋∠APG＝∠APG＋∠CPH＝90°，
∴∠GAP＝∠CPH，
∴△APG∽△PCH，
∴＝，即＝，
整理得：t2﹣(m＋2)t＋2m＋4n＋16＝0，
∵恰好存在3个P点使得△PAC为直角三角形，而当∠PAC＝90°或∠ACP＝90°时，均有且仅有一个点P存在，
∴当∠APC＝90°时，有且只有一个点P存在，即关于t的一元二次方程有两个相等实数根，
∴△＝(m＋2)2﹣4(2m＋4n＋16)＝0，
∴n＝，
又∵点C(m，n)是对称轴右侧的抛物线上的一定点，
∴n＝m2﹣8m＋12，
∴m2﹣8m＋12＝，
整理得15m2﹣124m＋252＝0，
解得：m1＝eq \f(14,3)，m2＝eq \f(18,5)，
∵eq \f(18,5)＜4，m2＝eq \f(18,5)不符合题意，舍去，
∴m＝eq \f(14,3)，此时n＝(eq \f(14,3))2﹣8×eq \f(14,3)＋12＝﹣，
∴C(eq \f(14,3)，﹣)，
将m＝eq \f(14,3)，n＝﹣，代入t2﹣(m＋2)t＋2m＋4n＋16＝0，
整理得：t2﹣eq \f(20,3)t＋eq \f(100,9)＝0，解得：t1＝t2＝eq \f(10,3)，
∴P(eq \f(10,3)，﹣4)；
②当∠PAC＝90°时，如图(2)②，
过点C作CT⊥x轴于点T，过点P作PR⊥x轴于点R，
则AT＝eq \f(14,3)﹣2＝eq \f(8,3)，CT＝，PR＝4，AR＝2﹣t，
∠ATC＝∠PRA＝∠PAC＝90°，
∴∠PAR＋∠APR＝∠PAR＋∠CAT＝90°，
∴∠APR＝∠CAT，
∴△APR∽△CAT，
∴＝，即＝，
解得：t＝﹣eq \f(10,3)，∴P(﹣eq \f(10,3)，﹣4)；
③当∠ACP＝90°时，如图(2)③，
过点C作KH⊥x轴于点H，交直线MN于点K，
则∠AHC＝∠CKP＝∠ACP＝90°，
CH＝，AH＝，CK＝4﹣＝，PK＝﹣t，
∵∠ACH＋∠CAH＝∠ACH＋∠PCK＝90°，
∴∠CAH＝∠PCK，
∴△CAH∽△PCK，
∴＝，
∴AH•PK＝CK•CH，即(﹣t)＝×，
解得：t＝，∴P(，﹣4)；
综上所述，
C点坐标为(，﹣)，P点的坐标为(，﹣4)或(﹣，﹣4)或(，﹣4)．
解：(1)将点A(﹣2，0)、B(6，0)、C(0，﹣3)代入y＝ax2＋bx＋c，
得，解得，
∴y＝eq \f(1,4)x2﹣x﹣3；
(2)如图1，过点A作AE⊥x轴交直线BC于点E，过P作PF⊥x轴交直线BC于点F，
∴PF∥AE，
∴＝，
设直线BC的解析式为y＝kx＋d，
∴，∴，
∴y＝eq \f(1,2)x﹣3，
设P(t，eq \f(1,4)t2﹣t﹣3)，则F(t，eq \f(1,2)t﹣3)，
∴PF＝eq \f(1,2)t﹣3﹣eq \f(1,4)t2＋t＋3＝﹣eq \f(1,4)t2＋eq \f(3,2)t，
∵A(﹣2，0)，
∴E(﹣2，﹣4)，
∴AE＝4，
∴＝＝＝﹣t2＋t＝﹣(t﹣3)2＋，
∴当t＝3时，有最大值，
∴P(3，﹣eq \f(15,4))；
(3)∵P(3，﹣eq \f(15,4))，D点在l上，
如图2，当∠CBD＝90°时，
过点B作GH⊥x轴，过点D作DG⊥y轴，DG与GH交于点G，过点C作CH⊥y轴，CH与GH交于点H，
∴∠DBG＋∠GDB＝90°，∠DBG＋∠CBH＝90°，
∴∠GDB＝∠CBH，
∴△DBG∽△BCH，
∴＝，即＝，
∴BG＝6，
∴D(3，6)；
如图3，当∠BCD＝90°时，
过点D作DK⊥y轴交于点K，
∵∠KCD＋∠OCB＝90°，∠KCD＋∠CDK＝90°，
∴∠CDK＝∠OCB，
∴△OBC∽△KCD，
∴＝，即＝，
∴KC＝6，
∴D(3，﹣9)；
如图4，当∠BDC＝90°时，
线段BC的中点T(3，﹣eq \f(3,2))，BC＝3eq \r(5)，设D(3，m)，
∵DT＝eq \f(1,2)BC，∴|m＋eq \f(3,2)|＝eq \f(3,2)eq \r(5)，
∴m＝eq \f(3,2)eq \r(5)﹣eq \f(3,2)或m＝﹣eq \f(3,2)eq \r(5)﹣eq \f(3,2)，
∴D(3，eq \f(3,2)eq \r(5)﹣eq \f(3,2))或D(3，﹣eq \f(3,2)eq \r(5)﹣eq \f(3,2))；
综上所述：△BCD是直角三角形时，
D点坐标为(3，6)或(3，﹣9)或(3，﹣eq \f(3,2)eq \r(5)﹣eq \f(3,2))或(3，eq \f(3,2)eq \r(5)﹣eq \f(3,2))．
解：(1)将M(﹣2，﹣2)代入抛物线解析式得：
﹣2＝eq \f(1,a)(﹣2﹣2)(﹣2＋a)，解得：a＝4；
(2)①由(1)抛物线解析式y＝eq \f(1,4)(x﹣2)(x＋4)，
当y＝0时，得：0＝eq \f(1,4)(x﹣2)(x＋4)，解得：x1＝2，x2＝﹣4，
∵点B在点C的左侧，
∴B(﹣4，0)，C(2，0)，
当x＝0时，得：y＝﹣2，即E(0，﹣2)，
∴S△BCE＝eq \f(1,2)×6×2＝6；
②由抛物线解析式y＝eq \f(1,4)(x﹣2)(x＋4)，得对称轴为直线x＝﹣1，
根据C与B关于抛物线对称轴直线x＝﹣1对称，连接BE，与对称轴交于点H，即为所求，
设直线BE解析式为y＝kx＋b，
将B(﹣4，0)与E(0，﹣2)代入得：
，解得：，
∴直线BE解析式为y＝﹣eq \f(1,2)x﹣2，
将x＝﹣1代入得：y＝eq \f(1,2)﹣2＝﹣eq \f(3,2)，则H(﹣1，﹣eq \f(3,2))．
解：(1)当x＝0，y＝3，∴C(0，3).
设抛物线的解析式为y＝a(x＋1)(x﹣eq \f(3,2)).
将C(0，3)代入得：﹣eq \f(3,2)a＝3，解得：a＝﹣2，
∴抛物线的解析式为y＝﹣2x2＋x＋3.
(2)过点B作BM⊥AC，垂足为M，过点M作MN⊥OA，垂足为N.
∵OC＝3，AO＝1，
∴tan∠CAO＝3.
∴直线AC的解析式为y＝3x＋3.
∵AC⊥BM，
∴BM的一次项系数为﹣eq \f(1,3).
设BM的解析式为y＝﹣eq \f(1,3)x＋b，将点B的坐标代入得：﹣eq \f(1,3)×eq \f(3,2)＋b＝0，解得b＝eq \f(1,2).
∴BM的解析式为y＝﹣eq \f(1,3)x＋eq \f(1,2).
将y＝3x＋3与y＝﹣eq \f(1,3)x＋eq \f(1,2)联立解得：x＝﹣eq \f(3,4)，y＝eq \f(3,4).
∴MC＝BM＝eq \f(3,4)eq \r(10).
∴△MCB为等腰直角三角形.
∴∠ACB＝45°.
(3)如图2所示：延长CD，交x轴与点F.
∵∠ACB＝45°，点D是第一象限抛物线上一点，
∴∠ECD＞45°.
又∵△DCE与△AOC相似，∠AOC＝∠DEC＝90°，
∴∠CAO＝∠ECD.
∴CF＝AF.
设点F的坐标为(a，0)，则(a＋1)2＝32＋a2，解得a＝4.
∴F(4，0).
设CF的解析式为y＝kx＋3，将F(4，0)代入得：4k＋3＝0，解得：k＝﹣eq \f(3,4).
∴CF的解析式为y＝﹣eq \f(3,4)x＋3.
将y＝﹣eq \f(3,4)x＋3与y＝﹣2x2＋x＋3联立：解得：x＝0(舍去)或x＝eq \f(7,8).
将x＝eq \f(7,8)代入y＝﹣eq \f(3,4)x＋3得：
y＝. ∴D(，).
解：(1)根据题意得：6＝﹣eq \f(1,2)×32＋3b，解得：b＝eq \f(7,2)，
∴抛物线的解析式为：y＝﹣eq \f(1,2)x2＋eq \f(7,2)x；
(2)过点P作PE⊥x轴，垂足为点E，如图：
∵点P在抛物线y＝﹣eq \f(1,2)x2＋eq \f(7,2)x上，点P的横坐标为t，
∴P(t，﹣eq \f(1,2)t2＋eq \f(7,2)t)，∴PE＝﹣eq \f(1,2)t2＋eq \f(7,2)t，
在y＝﹣eq \f(1,2)x2＋eq \f(7,2)x中，令y＝0，得﹣eq \f(1,2)x2＋eq \f(7,2)x＝0，解得x1＝0，x2＝7，
∴点A的坐标为(7，0)，∴S＝eq \f(1,2)OAPE＝eq \f(1,2)×7(﹣eq \f(1,2)t2＋eq \f(7,2)t)＝﹣eq \f(7,4)t2＋12.25t；
答：S与t的函数解析式为S＝﹣eq \f(7,4)t2＋12.25t；
(3)过点P作PE⊥x轴，垂足为点E，过点B作FG⊥y轴，垂足为点F，FG交EP的延长线于点G，取OD的中点M，连接BM，CM，延长BM交x轴于点N，延长CM至点H，如图：，
当S＝17.5时，17.5＝﹣t2＋12.25t，
解得t1＝2，t2＝5，
∵抛物线y＝﹣eq \f(1,2)x2＋eq \f(7,2)x的对称轴为直线x＝eq \f(7,2)，点P在对称轴的右侧，
∴t＝5，
∴点P的坐标为(5，5)，
∵FG⊥y轴，
∴∠BFO＝∠PEA＝90°，
又∵∠FOA＝90°，
∴∠BFO＋∠FOA＝180°，
∴FG∥OA，
∴∠G＝∠PEA＝90°，
∵点P的坐标为(5，5)，
∴PE＝OE，
∴∠POE＝∠OPE＝45°，
∵B(3，6)，
∴BG＝2，PG＝1，
在Rt△OBF中，，
在Rt△PBG中，，
∴tan∠BOF＝tan∠PBG，
∴∠BOF＝∠PBG，
又∵∠BOF＋∠OBF＝90°，
∴∠PBG＋∠OBF＝90°，
∴∠OBP＝90°，
设∠CBD＝2α，
∵∠ODB-eq \f(1,2)∠CBD=∠AOP，
∴∠ODB＝eq \f(1,2)∠CBD＋POA＝α＋45°，
∵∠OBD＝∠OCD＝90°，
∴BM＝OM＝DM＝CM，
∴∠MBD＝∠BDM＝α＋45°，
∴∠MCB＝∠MBC＝α＋45°﹣2α＝45°﹣α，∠OMN＝∠BMD＝180°﹣2(α＋45°)＝90°﹣2α，∠BMO＝2α＋90°，
∴∠BMH＝∠MCB＋∠MBC＝90°﹣2α，
∴∠OMH＝∠BMO﹣∠BMH＝(2α＋90°)﹣(90°﹣2α)＝4α，
∴∠CMN＝180°﹣∠OMH﹣∠OMN＝180°﹣4α﹣(90°﹣2α)＝90°﹣2α＝∠OMN，
∵OM＝CM，
∴BN⊥x轴，CN＝ON，
∴CN＝ON＝3，
∴OC＝6，
∴点C的坐标为(6，0)．
(1)解：AP=2t∵∠EDF=90°，∠DEF=45°，
∴∠CQE=45°=∠DEF，∴CQ=CE=t，∴AQ=8﹣t，
t的取值范围是：0≤t≤5；
(2)过点P作PG⊥x轴于G，可求得AB=10，SinB=，PB=10﹣2t，EB=6﹣t，
∴PG=PBSinB=(10﹣2t)
∴y=S△ABC﹣S△PBE﹣S△QCE==
∴当(在0≤t≤5内)，y有最大值，y最大值=(cm2)

(3)若AP=AQ，则有2t=8﹣t解得：t=eq \f(8,3)(s)
若AP=PQ，如图①：过点P作PH⊥AC，则AH=QH=，PH∥BC
∴△APH∽△ABC，∴，即，
解得：(s)若AQ=PQ，如图②：过点Q作QI⊥AB，则AI=PI=AP=t
∵∠AIQ=∠ACB=90°∠A=∠A，
∴△AQI∽△ABC∴即，解得：(s)
综上所述，当或或时，△APQ是等腰三角形．