数学必修 第二册8.4 空间点、直线、平面之间的位置关系教课ppt课件

这是一份数学必修 第二册8.4 空间点、直线、平面之间的位置关系教课ppt课件，共35页。PPT课件主要包含了不在一条直线上，两个点，l⊂α，公共直线等内容，欢迎下载使用。
| 自 学 导 引 |
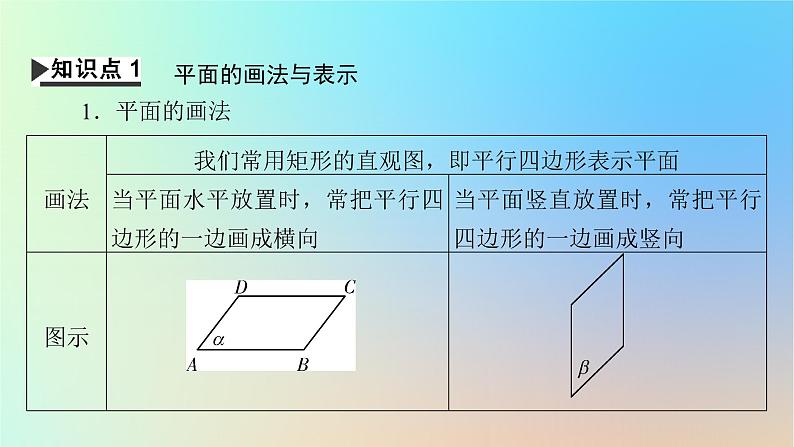
　　　　平面的画法与表示1．平面的画法
2．平面的表示方法(1)用希腊字母表示，如平面α，平面β，平面γ；(2)用代表平面的平行四边形的四个顶点的大写英文字母表示，如平面ABCD；(3)用代表平面的平行四边形的相对的两个顶点的大写英文字母表示，如平面AC，平面BD．
【预习自测】有下列说法：①书桌面是平面；②8个平面重叠后，要比6个平面重叠后厚；③有一个平面的长是100 m，宽是 90 m；④平面是绝对平滑，无厚度，无限延展的抽象概念．其中正确的个数为(　　)A．0　　　　　B．1　　　　C．2　　　　　D．3【答案】B【解析】①错误，因为平面具有延展性；②错误，平面无厚度；③错误，因为平面无厚度、大小之分；④正确，符合平面的概念．
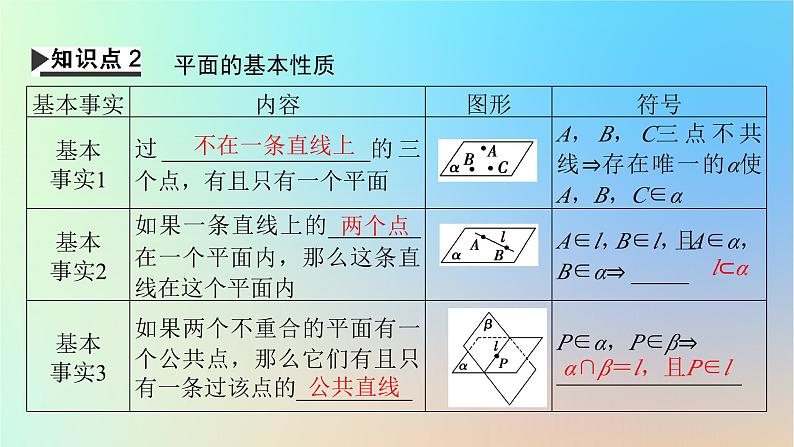
　　　　平面的基本性质
α∩β＝l，且P∈l　
特别提醒三个推论：推论1：经过一条直线和这条直线外一点，有且只有一个平面．推论2：经过两条相交直线，有且只有一个平面．推论3：经过两条平行直线，有且只有一个平面．
【预习自测】判断下列命题是否正确．(正确的画“√”，错误的画“×”)(1)三点可以确定一个平面．(　　)(2)一条直线和一个点可以确定一个平面．(　　)(3)四边形是平面图形．(　　)(4)两条相交直线可以确定一个平面．(　　) 【答案】(1)×　(2)×　(3)×　(4)√
【解析】(1)不共线的三点可以确定一个平面．(2)一条直线和这条直线外一个点可以确定一个平面．(3)四边形不一定是平面图形．(4)两条相交直线可以确定一个平面．
| 课 堂 互 动 |
题型1　立体几何三种语言的相互转化　　　　用符号表示下列语句，并画出图形．(1)平面α与β相交于直线l，直线a与平面α，β分别相交于点A，B；(2)点A，B在平面α内，直线a与平面α交于点C，点C不在直线AB上．
解：(1)用符号表示：α∩β＝l，a∩α＝A，a∩β＝B，如图1．(2)用符号表示：A∈α，B∈α，a∩α＝C，C∉AB，如图2．
三种语言的转换的注意点(1)用文字语言、符号语言表示一个图形时，首先注意观察图形有几个平面、几条直线且相互之间的位置关系如何，试着先用文字语言表示，再用符号语言表示．(2)要注意符号语言的意义．如点与直线的位置关系只能用“∈”或“∉”，直线与平面的位置关系只能用“⊂”或“⊄”．(3)由符号语言或文字语言画相应的图形时，要注意实线和虚线的区别．
1．用符号语言表示下列语句，并画出图形：(1)三个平面α，β，γ相交于一点P，且平面α与平面β相交于PA，平面α与平面γ相交于PB，平面β与平面γ相交于PC；(2)平面ABD与平面BDC相交于BD，平面ABC与平面ADC相交于AC．
解：(1)符号语言表示：α∩β∩γ＝P，α∩β＝PA，α∩γ＝PB，β∩γ＝PC，如图1．(2)符号语言表示：平面ABD∩平面BDC＝BD，平面ABC∩平面ADC＝AC，如图2．
图1　　　　　　　　图2
题型2　点线共面问题　　　　如图，已知：a⊂α，b⊂α，a∩b＝A，P∈b，PQ∥a．求证：PQ⊂α．证明：∵PQ∥a，∴PQ与a确定一个平面β．∴a⊂β，P∈β．∵P∈b，b⊂α，∴P∈α．又∵a⊂α，∴α与β重合．∴PQ⊂α．
解决点线共面问题的基本方法
2．如图，已知直线a∥b∥c，l∩a＝A，l∩b＝B，l∩c＝C．求证：直线a，b，c和l共面．
证明：(方法一：辅助平面法)因为a∥b，所以a，b确定一个平面α．因为A∈a，B∈b，所以A∈α，B∈α．又因为A∈l，B∈l，所以l⊂α．因为C∈l，所以C∈α，所以直线a与点C同在平面α内．因为a∥c，所以直线a，c确定一个平面β．因为C∈c，c⊂β，所以C∈β，即直线a与点C同在平面β内．由推论1，可得平面α和平面β重合，则c⊂α．所以a，b，c，l共面．
(方法二：纳入平面法)因为a∥b，所以a，b确定一个平面α．因为A∈a，B∈b，所以A∈α，B∈α．又因为A∈l，B∈l，所以l⊂α．故a，b，l都在平面α内，即b在a，l确定的平面内．同理可证c在a，l确定的平面内．因为过a与l只能确定一个平面，所以a，b，c，l共面于a，l确定的平面．
题型3　点共线、线共点问题　　　　如图，已知平面α，β，且α∩β＝l．设梯形ABCD中，AD∥BC，且AB⊂α，CD⊂β．求证：AB，CD，l共点(相交于一点)．
证明：因为梯形ABCD中，AD∥BC，所以AB，CD是梯形ABCD的两腰．所以AB，CD必定相交于一点．设AB∩CD＝M．又因为AB⊂α，CD⊂β，所以M∈α，M∈β．所以M∈α∩β．又因为α∩β＝l，所以M∈l．即AB，CD，l共点(相交于一点)．
证明点共线的方法(1)首先找出两个平面，然后证明这些点都是这两个平面的公共点，根据基本事实3可知，这些点都在两个平面的交线上．(2)选择其中两点确定一条直线，然后证明其他点也在此直线上．证明三线共点的步骤(1)首先说明两条直线共面且交于一点．(2)说明这个点在另两个平面上，并且这两个平面相交．(3)得到交线也过此点，从而得到三线共点．
3．如图，在四边形ABCD中，已知AB∥CD，直线AB，BC，AD，DC分别与平面α相交于点E，G，H，F．求证：E，F，G，H四点必定共线．
证明：∵AB∥CD，∴AB，CD确定一个平面β．又∵AB∩α＝E，AB⊂β，∴E∈α，E∈β，即E为平面α与平面β的一个公共点．同理可证F，G，H均为平面α与β的公共点．∵两个平面有公共点，它们有且只有一条通过公共点的公共直线，∴E，F，G，H四点必定共线．
易错警示　应用公理或其推论时忽略条件致误　　　　已知A，B，C，D，E五点中，A，B，C，D共面，B，C，D，E共面，则A，B，C，D，E五点一定共面吗？错解：A，B，C，D，E五点一定共面．因为A，B，C，D共面，所以点A在B，C，D所确定的平面内．因为B，C，D，E共面，所以点E也在B，C，D所确定的平面内．所以点A，E都在B，C，D所确定的平面内，即A，B，C，D，E五点一定共面．易错防范：错解忽略了基本事实1中“不在一条直线上的三点”这个重要条件．实际上B，C，D三点有可能共线．
正解：①如果B，C，D三点不共线，则B，C，D三点确定一个平面α．因为A，B，C，D共面，所以点A在平面α内．因为B，C，D，E共面，所以点E在平面α内．所以点A，E都在平面α内，即A，B，C，D，E五点一定共面．②如果B，C，D三点共线于l，若A∈l，E∈l，则A，B，C，D，E五点一定共面；若A，E中有且只有一个在l上，则A，B，C，D，E五点一定共面；若A，E都不在l上，则A，B，C，D，E五点可能不共面．
| 素 养 达 成 |
1．立体几何的三种语言．(体现逻辑推理、直观想象核心素养)图形语言、符号语言、文字语言是立体几何的三大语言，要准确实现这三种语言的相互转换．
2．三个基本事实的作用：基本事实1——判定点共面、线共面的依据；基本事实2——判定直线在平面内的依据；基本事实3——判定点共线、线共点的依据．3．证明几点共线的方法：首先考虑两个平面的交线，再证有关的点都是这两个平面的公共点．或先由某两点作一条直线，再证明其他点也在这条直线上．
1．(题型2)能确定一个平面的条件是(　　)A．空间三个点B．一个点和一条直线C．无数个点D．两条相交直线【答案】D【解析】不在同一条直线上的三个点可确定一个平面，A，B，C条件不能保证有不在同一条直线上的三个点，故不正确．
2．(题型1)若直线a⊂平面α，直线b⊂平面α，M∈a，N∈b，M∈l，N∈l，则(　　)A．l⊂αB．l⊄αC．l∩α＝MD．l∩α＝N【答案】A【解析】因为M∈a，a⊂α，所以M∈α，同理，N∈α．又因为M∈l，N∈l，故l⊂α．
3．(题型2，3)如果空间四点A，B，C，D不共面，那么下列判断中正确的是(　　)A．A，B，C，D四点中必有三点共线B．A，B，C，D四点中不存在三点共线C．直线AB与CD相交D．直线AB与CD平行【答案】B【解析】两条平行直线、两条相交直线、直线及直线外一点都分别确定一个平面．
4．(题型1)设平面α与平面β交于直线l，A∈α，B∈α，且直线AB∩l＝C，则直线AB∩β＝_______．【答案】C【解析】∵α∩β＝l，AB∩l＝C，∴C∈β，C∈AB．∴AB∩β＝C．