北师大版数学七年级下册 2.1.1《两条直线的位置关系》第1课时 课件+分层练习（含答案解析）

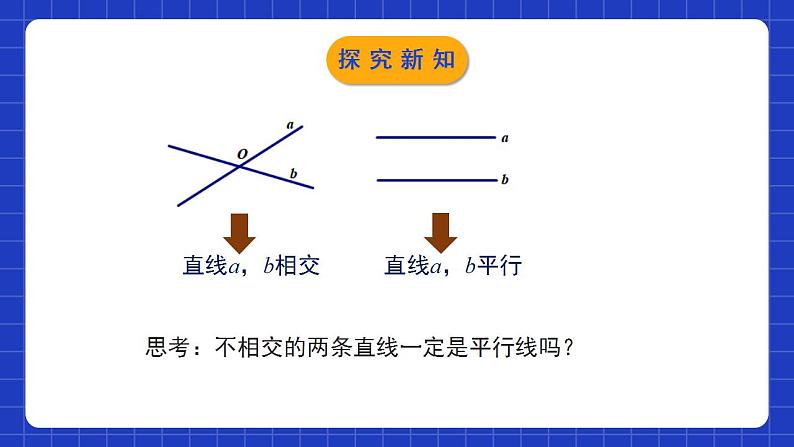
2.1.1两条直线的位置关系第1课时学习目标1通过观看图片，能说出同一平面内两条直线的位置关系，认识平行线与相交线；2通过观察、测量、说理等过程，认识对顶角，探索出“对顶角相等”的性质；3通过具体情境，认识补角、余角，探索其性质并能解决简单的实际问题. 观察下面的几幅生活中的图片，想想在同一平面内，两条直线的位置关系都有哪两种？情境导入情境导入相交线、平行线的概念结合图像说说平面内两条直线的位置关系有哪些1.若两条直线只有一个公共点，我们称这两条直线为相交线.2.在同一平面内，不相交的两条直线叫做平行线.探究新知思考：不相交的两条直线一定是平行线吗？探究新知 在同一平面内，两条直线的位置关系有相交和平行两种.既不相交也不平行探究新知练一练：下列说法正确是（ ）.A.在同一平面内，不相交的两条射线是平行线B.在同一平面内，两条直线不相交就重合C.在同一平面内，没有公共点的两条直线是平行线D.不相交的两条直线是平行线直线平行在同一平面内C探究新知对顶角的概念及性质如图，直线AB与CD相交于O，1234∠1和∠2有什么位置关系？有什么大小关系？位置关系：1.∠1和∠2有公共顶点O；2.∠1和∠2的两边互为反向延长线..∠1和∠2互为对顶角.探究新知1234对顶角的定义：有公共顶点，且两边互为反向延长线的两个角叫做对顶角.∠1和∠2，∠3和∠4.图中的对顶角有：探究新知1234对顶角的性质：对顶角相等.∠1和∠2有什么大小关系？猜想：∠1=∠2验证：因为∠AOB=∠COD=180°，所以∠2+∠3=180°，∠1+∠3=180°.所以∠1=∠2.所以∠2=180°-∠3，∠1=180°-∠3.探究新知练一练：下列各图中，∠1和∠2是对顶角的是（ ）DDCBA探究新知补角和余角的概念与性质图中，∠1和∠2是对顶角，∠3和∠4也是对顶角。1234∠1和∠3又有什么数量关系呢？∠1+∠3=180° 定义：如果两个角的和是180º，那么称这两个角互为补角.简称这两个角互补.∠1和∠3互补，∠1和∠4也互补.探究新知1234 图中，∠1和∠3有一条公共边，另一边互为反向延长线，这样的两个角叫做互为邻补角.∠1和∠3互为邻补角，∠1和∠4也互为邻补角.注意：两个角互补指的是两个角的数量关系，与位置无关！探究新知 如果两个角的和是90°，那么称这两个角互为余角.注：两个角不一定有公共边.探究新知 如图，打台球时，选择适当的方向，用白球击打红球，反弹后的红球会直接入袋，此时∠1=∠2.实景图几何图形探究新知 如图，ON与DC交于点O，∠DON=∠CON=90︒，∠1=∠2.（1）有哪些角互为补角？有哪些角互为余角？（2）∠3与∠4有什么关系？为什么？（3）∠AOC与∠BOD有什么关系？为什么？探究新知（1）有哪些角互为补角？有哪些角互为余角？解： ∠1与∠AOC互补，∠2与∠BOD互补；∠1与∠3互余，∠2与∠4互余. 如图，ON与DC交于点O，∠DON=∠CON=90︒，∠1=∠2.探究新知 如图，ON与DC交于点O，∠DON=∠CON=90︒，∠1=∠2.（2）∠3与∠4有什么关系？为什么？理由：因为 ∠DON=∠CON=90︒，结论：∠3=∠4所以 ∠3=90︒-∠1，∠4=90︒-∠2.因为∠1=∠2，所以∠3=∠4.性质：同角或等角的余角相等.探究新知 如图，ON与DC交于点O，∠DON=∠CON=90︒，∠1=∠2.（3）∠AOC与∠BOD有什么关系？为什么？理由：因为 ∠DOC=180︒，结论：∠AOC=∠BOD所以 ∠AOC=180︒-∠1， 因为 ∠1=∠2，所以 ∠AOC=∠BOD. ∠BOD=180︒-∠2.性质：同角或等角的补角相等.探究新知归纳总结同角或等角的余角相等同角或等角的补角相等互余与互补只与角的数值有关，与位置无关。而对顶角是根据角的位置来判断的探究新知1. 下列图形中，∠1与∠2是对顶角的是(　　)B随堂练习2．已知，∠α＝35°，则∠α的余角的度数是(　　)A．55° B．65° C．145° D．155° A3. 如果一个角的补角是120°，那么这个角是(　　)A. 150° B. 90° C. 60° D. 30°C随堂练习4. 如图，直线AB，CD，EF相交于点O，则∠1＋∠2＋∠3等于(　　)A. 90°B. 150°C. 180°D. 210°,C随堂练习5．如图，∠1与∠2不是互余关系的是(　　)C随堂练习6. 图中是对顶角量角器，用它测量角的原理是________________．对顶角相等随堂练习7．如图，a，b相交于点O，∠2＝2∠1，求∠3的度数．解：∵O是直线a上的点∴∠1＋∠2＝180°又∵∠2＝2∠1∴2∠1＋∠1＝180°∴∠1＝60°∵∠1与∠3是对顶角∴∠3＝∠1＝60°随堂练习8．如图，∠AOB＝∠COD＝90°.(1)若∠1∶∠2＝2∶7，求∠1，∠2的度数；(2)试说明∠1和∠2的关系．随堂练习8．如图，∠AOB＝∠COD＝90°.(1)若∠1∶∠2＝2∶7，求∠1，∠2的度数；(2)试说明∠1和∠2的关系．(2)由(1)知∠1＋∠2＝180°，∴∠1与∠2互补．随堂练习1.同一平面内两线的位置关系：相交和平行2.对顶角及其性质：(1)对顶角的两边互为反向延长线，其实质是：对顶角是两直线相交所成的没有公共边的两个角.(2)性质：对顶角相等3.余角、补角及其性质(1)如果两个角的和为90°，那么称这两个角互为余角；如果两个角的和为180°，那么称这两个角互为补角.(2)性质：同角或等角的补角相等，同角或等角的补角相等.课堂小结课程结束