人教A版 (2019)必修 第二册9.2 用样本估计总体教课课件ppt

这是一份人教A版 (2019)必修 第二册9.2 用样本估计总体教课课件ppt，共32页。PPT课件主要包含了导入新课，精彩课堂，课堂练习，课堂总结等内容，欢迎下载使用。

9.2.1 总体取值规律的估计第1课时 频率分布表和频率分布直方图
《红楼梦》一书共120回,自从胡适作《红楼梦考证》以来,一般都认为前80回为曹雪芹所写,后40回为高鹗所续.能否从统计上作出论证?从1985年开始,复旦大学的李贤平教授带领他的学生做了这项很有意义的工作,他们创造性地将120回看成是120个样本,然后把与情节无关的虚词出现的次数作为变量,巧妙运用数理统计分析方法,将120回分成两类,即前80回为一类,后40回为一类,很形象地证实了《红楼梦》不是出自同一人的手笔.他们又找了一本曹雪芹的其他著作,做了类似计算,结果证实了用词手法完全相同,断定前80回为曹雪芹一人手笔.推翻了后40回是高鹗一个人所写,而是曹雪芹亲友将其草稿整理而成,宝黛故事为一人所写,贾府衰败情景当为另一人所写等等.这个论证在红学界轰动很大,使红学界大为赞叹.
统计学是通过收集数据和分析数据来认识未知现象的一门学科.面对一个统计问题,首先要根据实际需要收集样本,然后将样本数据进行整理分析,提取需要的信息,最后根据样本的情况来对总体的情况进行推理.
1.引出问题我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了减少水资源的浪费,计划对居民生活用水费用实施阶梯式水价制度,即确定一户居民月均用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.问题1 为什么要确定一个合理的居民月均用水量标准呢?每户居民月均用水量标准如果定得太低,会影响很多居民的日常生活;如果标准太高,则不利于节水.所以必须确定一个合理的用水标准.
问题2 你认为为了较为合理地确定出这个标准,需要做哪些工作?由于全市居民用户很多,全面调查存在时间和经费问题,所以通常采用抽样调查的方式,通过分析样本观测数据,来估计全市居民用户月均用水量的分布情况.
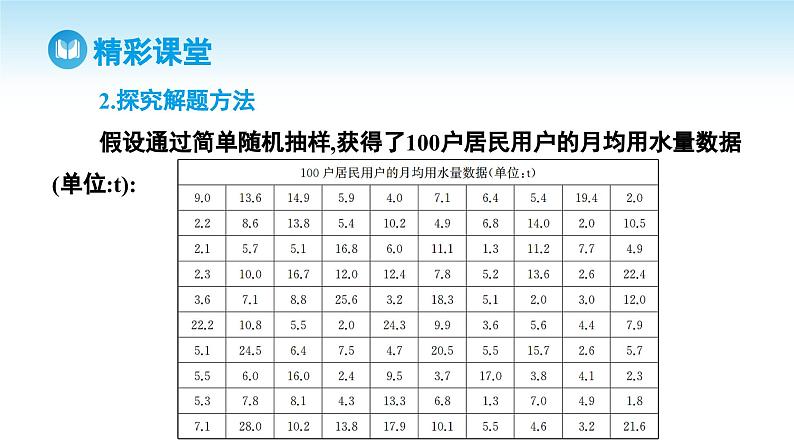
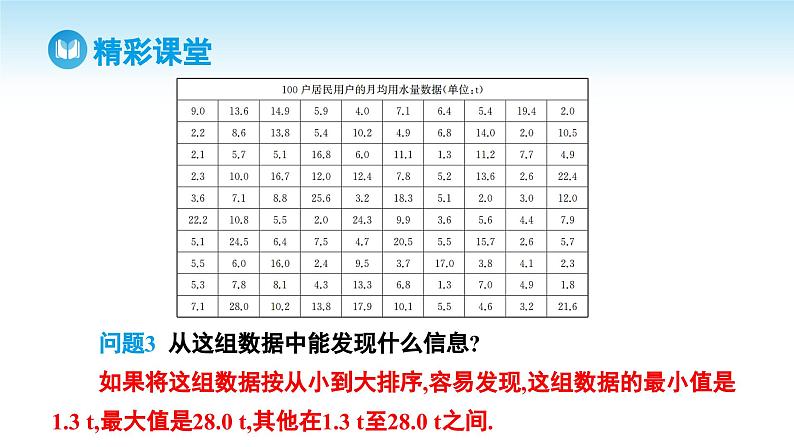
2.探究解题方法假设通过简单随机抽样,获得了100户居民用户的月均用水量数据(单位:t):
问题3 从这组数据中能发现什么信息?如果将这组数据按从小到大排序,容易发现,这组数据的最小值是1.3 t,最大值是28.0 t,其他在1.3 t至28.0 t之间.
问题4 面对多而杂乱的数据,我们往往无法直接从原始数据中找到它们所包含的信息.你有什么办法吗?为了更深入地挖掘数据蕴含的信息,探索数据的取值规律,我们需要对数据作进一步地整理与分析,一般采取两种方法:(1)用表格整理数据;(2)用图表示数据.
问题5 在初中都学过哪些能用来直观表示数据的图或表格?在以上问题中,应选择哪种图表来表示这组数据呢?在初中,曾用频数分布表和频数分布图来整理和表示这种数值型数据,由此能清楚地知道数据分布在各个小组的个数.在这个实际问题中,因为我们更关心月均用水量在不同范围内的居民占全市居民用户的比例,所以选择频率分布表和频率分布直方图来整理和表示数据.
3.类比作图,感受方法与画频数分布直方图类似,可以按以下步骤制作频率分布表、画频率分布直方图.第一步:求极差数据中最大值与最小值的差:28.0-1.3=26.7.
第二步:决定组距与组数问题6 为什么要对数据分组呢?不分组很难看出样本中的数字所包含的信息,分组后,计算出频率,从而估计总体的分布特征.问题7 数据分组要注意什么?注意:(1)数据分组可以是等距的,也可以是不等距的,要根据数据的特点而定.有时为了方便,往往按等距分组,或者除了第一和最后的两段,其他各段按等距分组.
第三步:将数据分组问题8 如何设定各组数据的范围呢?由于组距为3,9个组距的长度超过极差,我们可以使第一组的左端点略小于数据中的最小值,最后一组的右端点略大于数据中的最大值.例如,可以取区间为[1.2,28.2],按如下方式把样本观测数据以组距3分为9组:[1.2,4.2),[4.2,7.2),…,[25.2,28.2].
第四步:列频率分布表问题9 你能将这些数据用表格反映出来吗?
第五步:画频率分布直方图根据上表可以画出频率分布直方图,如图所示.
4.根据样本数据估计总体分布情况问题11 观察上述频率分布表和频率分布直方图,你觉得这组数据中蕴含了哪些有用的信息?你能发现居民用户月均用水量的哪些分布规律?你能用适当的语言描述吗?从频率分布表可以清楚地看出,样本观测数据落在各个小组的比例大小.例如,月均用水量在区间[4.2,7.2)内的居民用户最多,在区间[1.2,4.2)内的次之,而月均用水量超过16.2的各区间内数据所占比例较小,等等.
从频率分布直方图容易看出,居民用户月均用水量的样本观测数据的分布是不对称的,图形的左边高、右边低,右边有一个较长的“尾巴”.这表明大部分居民用户的月均用水量集中在一个较低值区域,尤其在区间[1.2,7.2)最为集中,少数用户居民的月均用水量偏多,而且随着月均用水量的增加,居民用户数呈现降低趋势.
有了样本观测数据的频率分布,我们可以用它估计总体的取值规律.根据100户居民用户的月均用水量的频率分布,可以推测该市全体居民用户月均用水量也会有类似的分布,即大部分居民用户月均用水量集中在较低值区域.这使我们确定用水量标准时,可以定一个合适的值,以达到既不影响大多数居民用户的水费支出,又能节水的目的.需要注意的是,由于样本的随机性,这种估计可能会存在一定误差,但这一误差一般不会影响我们对总体分布情况的大致了解.
5.不同的组数对于直方图呈现数据分布规律的影响探究 分别以3和27为组数,对数据进行等距分组,画出100户居民用户月均用水量的频率分布直方图,如图所示.观察图形,你发现不同的组数对于直方图呈现数据分布规律有什么影响?
同一组数据,组数不同,得到的直方图形状也不尽相同.
图1中直方图的组数少、组距大,从图中容易看出,数据分布的整体规律是随着月均用水量的增加,居民用户数的频率在降低,而且月均用水量在区间[1.2,10.2)内的居民用户数的频率,远大于在另两个区间[10.2,19.2)和[19.2,28.2)内的频率,这说明大部分居民用户的月均用水量都少于10.2 t.
图2中直方图的组数多、组距小,从图中可以看出,数据主要集中在低值区,尤其在区间[5.2,6.2)内最为集中.从总体上看,随着月均用水量的增加,居民用户数的频率呈下降趋势,但存在个别区间频率变大或者缺少的现象.
从上述分析可见,当频率分布直方图的组数少、组距大时,容易从中看出数据整体的分布特点,但由于无法看出每组内的数据分布情况,损失了较多的原始数据信息;当频率分布直方图的组数多、组距小时,保留了较多的原始数据信息,但由于小长方形较多,有时图形会变得非常不规则,不容易从中看出总体数据的分布特点.
注意:对于同一组数据,因为组距、组数不同而得到不同形状的直方图,会给人以不同的频率分布印象,这种印象有时会影响人们对总体的判断.因此,我们要注意积累数据分组、合理使用图表的经验.
回顾本节课所学内容,回答以下问题:(1)画频率分布表和频率分布直方图的步骤分别是什么?(2)频率分布直方图中,各小长方形的面积表示什么?各小长方形的面积总和等于多少?