高中数学人教B版 (2019)选择性必修 第二册第三章 排列、组合与二项式定理3.1 排列与组合3.1.2 排列与排列数说课课件ppt

这是一份高中数学人教B版 (2019)选择性必修 第二册第三章 排列、组合与二项式定理3.1 排列与组合3.1.2 排列与排列数说课课件ppt，共32页。PPT课件主要包含了新知初探·自主学习，课堂探究·素养提升，答案B，答案C等内容，欢迎下载使用。

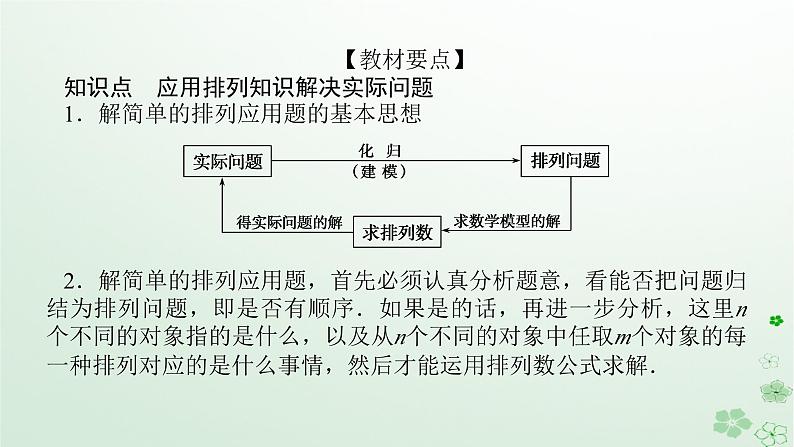
【教材要点】知识点　应用排列知识解决实际问题1．解简单的排列应用题的基本思想2．解简单的排列应用题，首先必须认真分析题意，看能否把问题归结为排列问题，即是否有顺序．如果是的话，再进一步分析，这里n个不同的对象指的是什么，以及从n个不同的对象中任取m个对象的每一种排列对应的是什么事情，然后才能运用排列数公式求解．
【基础自测】1．用数字1，2，3，4，5组成的无重复数字的四位偶数的个数为________．
2．A，B，C，D，E五人并排站成一排，如果A，B必须相邻且B在A的右边，那么不同的排法种数有________种．
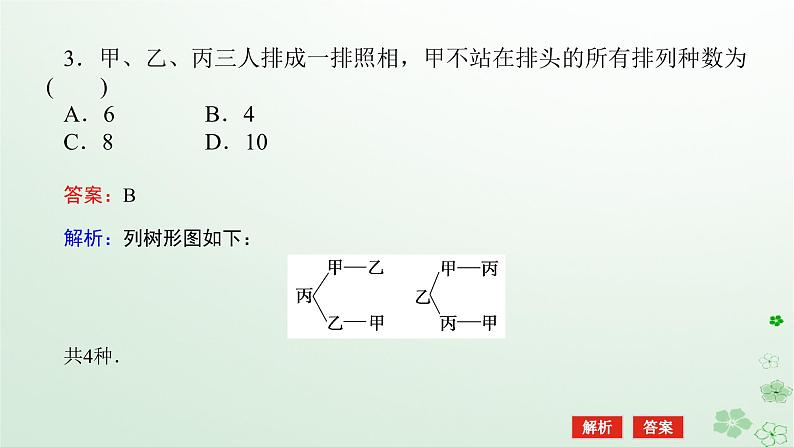
3．甲、乙、丙三人排成一排照相，甲不站在排头的所有排列种数为(　　)A．6　　　 B．4　　 C．8　　　 D．10
解析：列树形图如下：共4种．
4．6名学生排成两排，每排3人，则不同的排法种数为(　　)A．36　　　B．120 　 C．720　　 D．240
题型1　无限制条件的排列问题例1　(1)有5本不同的书，从中选3本送给3名同学，每人各1本，共有多少种不同的送法？(2)有5种不同的书，要买3本送给3名同学，每人各1本，共有多少种不同的送法？
状元随笔(1)从5本不同的书中选出3本分别送给3名同学，每人得到的书不同，属于求排列数问题；(2)给每人的书均可以从5种不同的书中任选1本，每人得到哪本书相互之间没有联系，要用分步乘法计数原理进行计算．
方法归纳1．没有限制的排列问题，即对所排列的对象或所排列的位置没有特别的限制，这一类问题相对简单，分清对象和位置即可．2．对于不属于排列的计数问题，注意利用计数原理求解．
跟踪训练1　(1)将3张电影票分给10人中的3人，每人1张，共有________种不同的分法．(2)从班委会5名成员中选出3名，分别担任班级学习委员、文娱委员与体育委员，不同的选法共有________种．
题型2　排队问题(“在”与“不在”“邻”与“不邻”“ 定序”问题)例2　(1)7名师生站成一排照相留念，其中老师1人，男学生4人，女学生2人，在下列情况下，各有多少种不同站法？①老师甲必须站在中间或两端；②2名女生必须相邻而站；③4名男生互不相邻；④若4名男生身高都不等，按从高到低的顺序站．
(2)从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的活动．若其中甲、乙两名志愿者不能从事翻译活动，则选派方案共有________种．
状元随笔　解决此类问题的方法主要按“优先”原则，即优先排特殊对象或优先考虑特殊位子，若一个位子安排的对象影响另一个位子的对象个数时，应分类讨论．
方法归纳解决排队问题时应注意的问题1．对于相邻问题可以采用捆绑的方法，将相邻的对象作为一个整体进行排列，但是要注意这个整体内部也要进行排列．2．对于不相邻问题可以采用插空的方法，先排没有限制条件的对象，再将不相邻的对象以插空的方式排入．3．对于顺序给定的对象的排列问题只需考虑其余对象的排列即可．4．“在”与“不在”的有限制条件的排列问题，既可以从对象入手，也可以从位置入手，原则是谁“特殊”谁优先．
跟踪训练2　3名男生，4名女生，按照不同的要求站成一排，求不同的排队方案有多少种．(1)甲不站中间，也不站两端；(2)甲、乙两人必须站两端；(3)男、女各站在一起；(4)男生必须排在一起；(5)男生不能排在一起；(6)男生互不相邻，且女生也互不相邻；(7)甲必须在乙的前面(不一定相邻)，则有多少种不同的排列方法？(8)甲、乙、丙三人自左向右的顺序不变(不一定相邻)，则有多少种不同的排列方法？(9)从包括甲、乙两名同学在内的7名同学中选出5名同学排成一列， 甲不在首位的排法有多少种？(10)从包括甲、乙两名同学在内的7名同学中选出5名同学排成一列，甲既不在首位，又不在末位的排法有多少种？
题型3　数字排列问题【思考探究】1．偶数的个位数字有何特征？从1，2，3，4，5中任取两个不同数字能组成多少个不同的偶数？[提示]　偶数的个位数字一定能被2整除．先从2，4中任取一个数字排在个位，共2种不同的排法，再从剩余数字中任取一个数字排在十位，共4种排法，故从1，2，3，4，5中任取两个数字，能组成2×4＝8(个)不同的偶数．
2．在一个三位数中，身居百位的数字x能是0吗？如果在0～9这十个数字中任取不同的三个数字组成一个三位数，如何排才能使百位数字不为0?[提示]　在一个三位数中，百位数字不能为0，在具体排数时，从对象0的角度出发，可先将0排在十位或个位的一个位置，其余数字可排百位、个位(或十位)位置；从“位置”角度出发可先从1～9这9个数字中任取一个数字排百位，然后再从剩余9个数字中任取两个数字排十位与个位位置．3．如何从26，17，31，48，19中找出大于25的数？[提示]　先找出十位数字比2大的数，再找出十位数字是2，个位数字比5大的数即可．
例3　用0，1，2，3，4，5这六个数字可以组成多少个无重复数字的：(1)六位奇数？(2)个位数字不是5的六位数？
状元随笔　这是一道有限制条件的排列问题，每一问均应优先考虑限制条件，遵循特殊对象或特殊位置优先安排的原则. 另外，还可以用间接法求解．
方法归纳解排数字问题常见的解题方法1．“两优先排法”：特殊对象优先排列，特殊位置优先填充．如“0”不排“首位”．2．“分类讨论法”：按照某一标准将排列分成几类，然后按照分类加法计数原理进行，要注意以下两点：一是分类标准必须恰当；二是分类过程要做到不重不漏．3．“排除法”：全排列数减去不符合条件的排列数．4．“位置分析法”：选排列问题按位置逐步讨论，把要求数字的每个数位排好．
跟踪训练3　用0，1，2，3，4，5这六个数取不同的数字组数．(1)能组成多少个无重复数字且为5的倍数的五位数？(2)能组成多少个无重复数字且比1 325大的四位数？