数学人教A版 (2019)8.6 空间直线、平面的垂直优秀课时训练

这是一份数学人教A版 (2019)8.6 空间直线、平面的垂直优秀课时训练，文件包含人教A版高中数学必修第二册同步培优讲义专题814空间直线平面的垂直二重难点题型检测教师版doc、人教A版高中数学必修第二册同步培优讲义专题814空间直线平面的垂直二重难点题型检测原卷版doc等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。

1．（3分）（2023·安徽蚌埠·统考二模）设，是两个不同的平面，a，b是两条不同的直线，下列说法正确的是（ ）
A．若，，，则B．若，，，则
C．若，，，则D．若，，，则
【解题思路】根据题意，由空间中直线与平面的位置关系对选项逐一判断，即可得到结果.
【解答过程】对于A，若，，，则，故正确；
对于B，若，，，则与相交或者，故错误；
对于C，若，，，则，故错误；
对于D，若，，，则与相交，不一定垂直，故错误.
故选:A.
2．（3分）（2023秋·北京西城·高二期末）在长方体中，，则二面角的余弦值为（ ）
A．B．C．D．
【解题思路】画出长方体，为二面角所成的平面角，求出的值即可得出答案.
【解答过程】长方体中，，，
，平面,平面,,
又平面 平面 ，
为二面角所成的平面角，
，
所以二面角的余弦值为.
故选：D.
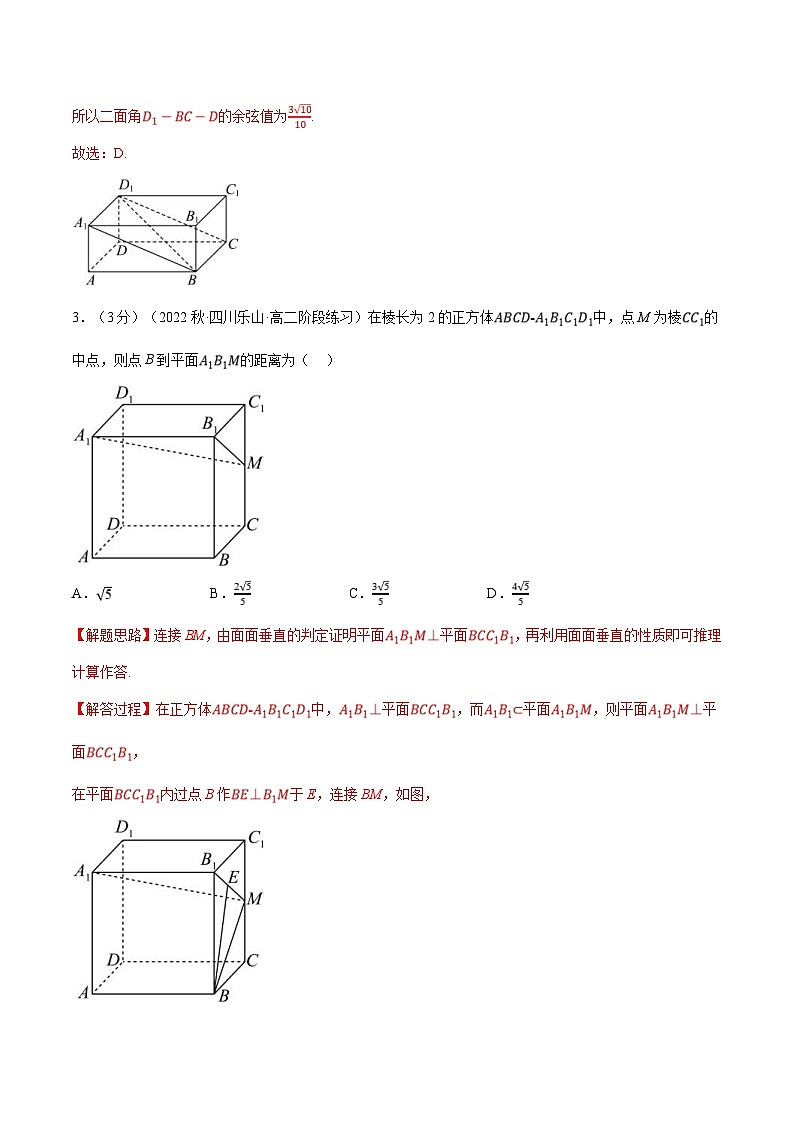
3．（3分）（2022秋·四川乐山·高二阶段练习）在棱长为2的正方体中，点M为棱的中点，则点B到平面的距离为（ ）
A．B．C．D．
【解题思路】连接BM，由面面垂直的判定证明平面平面，再利用面面垂直的性质即可推理计算作答.
【解答过程】在正方体中，平面，而平面，则平面平面，
在平面内过点B作于E，连接BM，如图，
因平面平面，于是得平面，则BE长即为点B到平面的距离，
点M为棱的中点，在中，，
，即，解得，
所以点B到平面的距离为.
故选：D.
4．（3分）（2022秋·山东潍坊·高二阶段练习）如图所示，平面矩形，且，下列结论中不正确的是（ ）
A．B．
C．D．
【解题思路】根据面面垂直的性质可得线面垂直，进而得线线垂直，由线线垂直，线面垂直以及面面垂直的互相转化即可根据选项逐一求解.
【解答过程】因为平面矩形，两平面交线为,,且平面，
所以平面，平面，所以，故D正确，
若，由于，,平面,则平面，平面,则这与为矩形矛盾，故A不正确；
因为平面矩形，两平面交线为,,平面，所以平面，平面,所以，故B正确，
由于平面，平面,所以，又，平面,所以平面,平面,所以,故C正确，
故选：A.
5．（3分）（2023·陕西西安·统考一模）在三棱锥，平面平面，是以为斜边的等腰直角三角形，为等边三角形，，则该三棱锥的外接球的表面积为（ ）
A．B．C．D．
【解题思路】由面面垂直的性质结合直角三角形和等边三角形的性质得出的外接圆圆心为该三棱锥的外接球的球心，再由正弦定理以及球的表面积公式求解.
【解答过程】解：过点作的垂线，垂足为，因为是以为斜边的等腰直角三角形，
所以的外接圆的圆心为，设的外接圆圆心为，其半径为，
则在上，所以，由面面垂直的性质可知，平面，
所以，即为该三棱锥的外接球的球心，
由正弦定理可知，，
故该三棱锥的外接球的表面积为.
故选：C.
6．（3分）（2023·全国·校联考模拟预测）已知正三棱柱的所有棱长都相等，，，分别是，，的中点，是线段上的动点，则下列结论中正确的个数是（ ）
①；②；③；④平面．
A．1B．2C．3D．4
【解题思路】连接，即可得到，再由正三棱柱的性质得到平面，即可得到，从而得到平面，再由线面垂直的性质得到，即可说明，即可判断①、②、③，连接，通过证明平面平面，即可说明④.
【解答过程】解：连接，因为正三棱柱的所有棱长都相等，所以，．
又，分别是，的中点，所以，所以．
因为，，，平面，所以平面．
又平面，所以．又，，平面，所以平面．
又平面，所以．
由题意知且，所以四边形是平行四边形，
所以，所以，故①、③正确；
与是异面直线，故②错误；
连接，因为，平面，平面，所以平面
又，同理可证平面，
又，平面，
所以平面平面．
因为是线段上的动点，所以平面，所以平面，故④正确．
故选：C.
7．（3分）（2023秋·北京石景山·高二期末）在直四棱柱中，底面为直角梯形，，点M在该四棱柱表面上运动，且满足平面平面．当线段的长度取到最大值时，直线与底面所成角的正弦值是（ ）
A．B．C．D．
【解题思路】根据直四棱柱的几何关系，利用面面垂直的判定定理找出点M在四棱柱表面上的运动轨迹，再根据线段的长度取到最大值时确定具体位置，根据几何法做出直线与底面所成的角，即可求得其正弦值.
【解答过程】根据几何体特征，四棱柱是直四棱柱，
所以平面，平面，所以，
要满足平面平面，作于，延长交于，交的延长线于，
作交于，连接，如下图所示；
又因为，所以平面，即平面
而平面，所以平面平面，
又因为点M在该四棱柱表面上运动，所以点M的轨迹是线段；
又因为底面为直角梯形，，
所以，即，得，所以；
又，所以，即为线段的中点，
，所以，
易知，当线段的长度取到最大值时，点于点重合，
此时，即为直线与底面所成的角，
，，
，
所以，线段的长度取到最大值时，直线与底面所成角的正弦值是.
故选：B.
8．（3分）（2022·河南·校联考一模）已知菱形ABCD的边长为2，，E是AD的中点，沿BE将折起至的位置，使，则下列结论中错误的是（ ）．
A．平面平面PDEB．平面平面PBC
C．平面平面BCDED．平面平面BCDE
【解题思路】根据线面、面面垂直的判断定理分析判断.
【解答过程】如图1，在菱形ABCD中，连接BD，则为等边三角形，且E是AD的中点，
∴，
如图2，在四棱锥中，，
，平面，
∴平面，
平面，则平面平面PDE，A正确；
∵，即，
∴，
，平面，
∴平面，
又∵，则平面，
平面，则平面平面PBC，B正确；
∵，
，平面，
∴平面，
平面，则平面平面BCDE，C正确；
∵平面，平面，则平面内不存在与平面垂直的直线，
∴平面不与平面垂直，D错误；
故选：D.
二．多选题（共4小题，满分16分，每小题4分）
9．（4分）（2023秋·河北·高三阶段练习）已知直线和平面，下列选项能得到成立的充分条件是（ ）
A．B．C．D．
【解题思路】根据线面及面面的位置关系结合面面垂直的判定定理逐项分析即得.
【解答过程】对于A，若，则与可能平行也可能相交，故A错误；
对于B，若，则，故B正确；
对于C，若，则与不一定垂直，故C错误；
对于D，由，可知在平面内必存在直线与平行，又，则，进而可得，故D正确.
故选：BD.
10．（4分）（2023秋·云南楚雄·高三期末）已知四棱锥的底面ABCD为矩形，平面PAB⊥平面ABCD，，，E为棱BP上一点，，且PA⊥AC，若四棱锥的每个顶点都在球O的球面上，且球O的体积为，则（ ）
A．B．
C．平面ADE⊥平面PABD．点E到平面PCD的距离为
【解题思路】根据面面垂直的性质、线面垂直的判定定理可判断C，由外接球的球心在中点，利用球的体积可求出，据此求出可判断B，再由勾股定理求出判断A，利用等体积法可求出E到平面PCD的距离判断D.
【解答过程】如图，则平面ADE⊥平面PAB，
因为平面PAB⊥平面ABCD，是交线，AD⊥AB，平面ABCD，
所以AD⊥平面PAB，因为平面ADE，则平面ADE⊥平面PAB，
又因为平面PAB，所以 AD⊥AP，
又因为PA⊥AC，，平面ABCD，所以PA⊥平面ABCD，
平面ABCD，所以，故 AD，AB，AP两两垂直，
所以是以AD，AB，AP为长、宽、高的长方体的对角线，
故侧棱PC为球O的直径，由，解得，
所以，解得，则，，故.
由，平面，所以AB⊥平面APD
又因为，所以CD⊥平面APD，
因为平面APD ，所以CD⊥PD，由勾股定理得.
设点E到平面PCD的距离为d，由，可知，过点E作EF⊥AB，垂足为F，则，且，
由，得，
解得.
综上，ACD正确，B错误.
故选：ACD.
11．（4分）（2022秋·江苏南京·高二阶段练习）(多选)如图，在三棱锥P-ABC中，已知PC⊥BC，PC⊥AC，点E，F，G分别是所在棱的中点，则下面结论中正确的是（ ）
A．平面EFG∥平面PBC
B．平面EFG⊥平面ABC
C．∠BPC是直线EF与直线PC所成的角
D．∠FEG是平面PAB与平面ABC所成二面角的平面角
【解题思路】分别用面面平行、面面垂直、线线角、二面角等知识对每个选项判断即可.
【解答过程】对于选项A：∵GF∥PC，GE∥CB，GF∩GE＝G，PC∩CB＝C，∴平面EFG∥平面PBC.故A正确；
对于选项B：∵PC⊥BC，PC⊥AC，PC∥GF，∴GF⊥BC，GF⊥AC，又BC∩AC＝C，∴GF⊥平面ABC，又平面，∴平面EFG⊥平面ABC. 故B正确；
对于选项C：由选项A知平面EFG∥平面PBC，且平面与两平面的交线分别为与，所以EF∥BP，∴∠BPC是直线EF与直线PC所成的角.故C正确；
对于选项D：∵GE与AB不垂直，∴∠FEG不是平面PAB与平面ABC所成二面角的平面角．故D错误.
故选：ABC.
12．（4分）（2023春·江苏南京·高三开学考试）如图，在五面体ABCDE中，平面ABCD⊥平面ABEF，四边形ABCD与四边形ABEF全等，且，，则下列说法正确的是（ ）
A．
B．若G为棱CE中点，则DF⊥平面ABG
C．若AD=CD，则平面ADE⊥平面BDE
D．若，则平面ADE⊥平面BCE
【解题思路】对于A，利用面面垂直的性质定理得到平面，从而得以判断；对于B，利用线面垂直的判定定理推得平面，由此判断即可；对于C，利用面面垂直的的判定定理，结合勾股定理即可判断；对于D，先证得与不重合，再推得平面平面，从而得到矛盾，由此判断即可.
【解答过程】对于A，因为平面平面ABEF，，平面平面，平面，
所以平面，因为平面，所以，故A正确；
对于B，取棱的中点，连接，如图①，
.
因为四边形ABCD与四边形ABEF全等，所以，
因为G为棱CE中点，所以，
因为，平面，所以平面，
由题意知，所以四边形为平行四边形，
所以，则平面，故B正确；
对于C，连接，如图①，
由题意知，所以，
又在直角梯形中易知，所以，即，
由选项A知，又平面，
所以平面，又平面，所以平面ADE⊥平面BDE，故C正确；
对于D，连接，过点作交的延长线于点，连接，如图②，
.
由，得，所以，
此时，
所以，故与不重合，
因为平面，平面，所以，
又，平面，所以平面，
又平面，所以平面平面，
假设平面平面，
因为与不重合，所以平面与平面不重合，
又平面平面，则平面，
因为平面，所以，
又，所以，这与矛盾，
所以假设不成立，故平面与平面不垂直，故D错误.
故选：ABC.
三．填空题（共4小题，满分16分，每小题4分）
13．（4分）（2022秋·青海海东·高二期中）若为一条直线，为三个互不重合的平面，给出下面四个命题：①，；②，；③，：④，．其中正确命题的序号有 ①③ ．
【解题思路】依据直线与平面、平面与平面的位置关系，找出反例逐一分析，即可得出答案.
【解答过程】
若，则又因为,所以则，①正确.
如果是长方体相对的两侧面,则它们都垂直底面,但这两个平面互相平行,故也可能平行,②不正确.
,则存在,,则由面面垂直的判定定理,③正确.
如果是长方体相邻的两侧面,为长方体不在这两个面内的侧棱, ,,也可能相交,④不正确.
综上，正确的命题的序号是①③.
故答案为:①③.
14．（4分）（2022秋·湖南郴州·高二阶段练习）如图所示，平面，，，，则二面角的余弦值大小为 0 .
【解题思路】作出二面角的平面角，求得相关线段的长，解三角形，即可求得答案.
【解答过程】作,垂足为D，作交于E点，连接,
因为，故D为的中点，E为的中点，
平面，平面，所以,
又，平面,
故平面,平面,故,
所以,则为二面角的平面角，
因为，,故,
则,
又平面，平面，所以,
则,故，
所以二面角的余弦值大小为0，
故答案为：0.
15．（4分）（2023·高三课时练习）如图，已知矩形ABCD所在的平面，则下列说法中正确的是 ①②③ ．（写出所有满足要求的说法序号）
①平面PAD⊥平面PAB； ②平面PAD⊥平面PCD；
③平面PBC⊥平面PAB； ④平面PBC⊥平面PCD．
【解题思路】根据线面垂直的性质定理及面面垂直的判定定理证明判断即可．
【解答过程】①由矩形ABCD所在的平面，所以，
又，且，平面，所以平面，
又平面，所以平面平面，故①正确；
②由矩形ABCD所在的平面，所以，
又，且，平面，所以平面，
又平面，所以平面平面，故②正确；
③由矩形ABCD所在的平面，所以，
又，且，平面，所以平面，
又平面，所以平面平面，故③正确；
④依题意得，若平面PBC⊥平面PCD，作交于，平面PBC平面PCD，所以平面PCD，又平面，所以,
因为，平面，所以平面，因为平面，所以,与矛盾，故④错误．
故答案为：①②③．
16．（4分）（2022·高一课时练习）如图，点P在正方体的面对角线上运动，则下面四个结论：①，点P到平面的距离不变；② 平面；③；④平面平面．其中正确结论的序号是 ①②④ ．（写出所有你认为正确结论的序号）
【解题思路】通过证明平面，平面，得平面平面，从而可判断②①，利用判断③，证明平面平面判断④．
【解答过程】连接．
因为，，
所以四边形是平行四边形，
所以．又平面平面，
所以平面．
同理可证平面，
又平面平面，且，
所以平面平面．
因为平面，
所以平面，故②正确．
因为平面，
所以平面，
所以点P到平面的距离不变，故①正确．
连接．
因为，
所以当P为的中点时才有，故③错误．
因为平面平面，
所以．
又，平面，
所以平面．
连接，又平面，
所以．
同理可证．
又平面平面，，
所以平面．又平面，
所以平面平面，故④正确．
故答案为：①②④．
四．解答题（共6小题，满分44分）
17．（6分）（2022·高一课时练习）如图，平面，，你能发现哪些平面互相垂直，为什么？
【解题思路】根据面面垂直的判定定理，先寻找线面垂直，再得面面垂直.
【解答过程】平面平面，平面平面，平面平面.
理由：平面，平面，平面，
∴平面平面，平面平面.
平面，平面，
.
又，,
平面.
平面，
∴平面平面.
18．（6分）（2022春·河南洛阳·高一阶段练习）如图，在正三棱柱中，是侧面对角线的交点，是侧面对角线的交点，是棱的中点．求证：
(1) 平面；
(2)平面平面
【解题思路】（1）连接和，证明，利用线面平行的判断定理即可证得平面；
（2）依题意，可证,从而可证得平面，利用面面垂直的判定定理即可证得平面平面．
【解答过程】（1）连接和，因为分别是侧面和侧面对角线的交点，
所以分别是和的中点．
所以,
又平面，平面，
故 平面﹔
（2）∵三棱柱为正三棱柱,
∴平面，平面，
∴，又，
∴,
又D是棱的中点，且为正三角形，所以．
由得,
而平面，所以平面，
又平面，故平面平面.
19．（8分）（2022秋·贵州安顺·高三期末）如图，四棱锥中，侧面为等边三角形且垂直于底面，，，是的中点.
(1)求证：平面平面；
(2)点在棱上，满足且三棱锥的体积为，求的值.
【解题思路】（1）连接，证明，继而证明平面，推得，从而证明平面，根据面面垂直的判定定理即可证明结论；
（2）由题意可推得，从而设点到平面的距离分别为，利用三棱锥等体积法分别求得，根据，即可求得答案.
【解答过程】（1）由题意底面， ,，
则底面为直角梯形，
连接 ，则,故四边形为矩形，
则 ， 所以四边形为正方形，所以 ，
因为侧面为等边三角形，O是 的中点，
所以 ，平面，
因为平面平面，平面平面，
所以平面，因为平面，
所以，因为平面 ，
所以平面，
因为平面 ，所以平面平面.
（2）因为底面中， ,，
侧面 为等边三角形，O是的中点，
所以,,, ，
因为平面，平面，
所以 ，
所以 ，
因为 ，
所以,所以 ,
设点到平面的距离分别为，
因为 ，所以 ,
即，故，
因为三棱锥的体积为，
所以 所以 ，解得，
所以，即
因为，所以 .
20．（8分）（2023·全国·高三专题练习）在边长为2的正方形外作等边（如图1），将沿折起到的位置，使得（如图2）.
(1)求证：平面平面；
(2)若F，M分别为线段的中点，求点P到平面的距离.
【解题思路】（1）通过证明平面来证得平面平面.
（2）利用等体积法来求点P到平面的距离.
【解答过程】（1）由于，所以，
由于四边形是正方形，所以，
由于平面，所以平面，
由于平面，
所以平面平面.
（2）连接，由于三角形是等边三角形，所以，
由于平面平面且交线为，平面，
所以平面.
由于是的中点，所以到平面的距离是，
且到平面的距离等于到平面的距离，设这个距离为.
由于平面，所以，
所以，，
在三角形中，由余弦定理得，
所以，，
在三角形中，，
则为锐角，，
所以，
，
由得，
解得，
所以点P到平面的距离为.
21．（8分）（2023秋·四川南充·高二期末）如图，在正三棱柱中，为上的点，为上的点，M，N分别为BA，BE的中点， 平面．
(1)证明：M，N，F，C四点共面，且平面平面；
(2)若，，求平面与平面所成锐二面角的余弦值．
【解题思路】（1）由题可得，进而M，N，F，C四点共面，然后根据线面垂直的判定定理可得平面，然后根据线面平行的性质定理及面面垂直的判定定理即可证出；
（2）取的中点，过点作的垂线交于，根据面面垂直的性质可得平面，进而可得为平面与平面所成二面角的平面角，然后结合条件即得解.
【解答过程】（1）证明：∵M、N分别为AB、BE的中点，
∴，
∵为正三棱柱，
∴,
∴,
∴M、N、F、C四点共面，
∵为正三棱柱，
∴平面平面，为等边三角形，
∵为的中点，
∴，又平面平面，平面，
∴平面，
∵平面平面，平面，平面，
∴，
∴平面，
∵平面，
∴平面平面；
（2）取的中点，过点作的垂线交于，连接，
由题可得，又平面平面，平面平面 ，平面，
所以平面，又平面，
∴，
∵，，平面，
∴平面，
∴为平面与平面所成二面角的平面角，
∵，，
∴，．
由（1）可得四边形为平行四边形，
∴，
∴，又，，
由得：，
所以，
∴，
∴平面与平面所成锐二面角的余弦值为.
22．（8分）（2022春·北京·高一期末）已知四棱锥的底面为直角梯形，平面，且，是棱上的动点.
（1）求证：平面平面；
（2）若平面，求的值；
（3）当是中点时，设平面与棱交于点，求截面的面积.
【解题思路】(1) 要证平面平面，只需证明平面，利用线面垂直的判定可证平面.
(2) 根据题意，作出点，再利用相似三角形求的值
(3) 从四点共面角度出发，利用平面向量基本定理确定点的位置，再求截面面积.
【解答过程】(1)证明：因为，所以，
又，所以.
因为平面，平面，所以.
又，在平面内，且相交于点，所以平面.
又平面，所以平面平面.
(2)

如图，连接，相交于点，过点作，交于点.
因为，平面，平面，所以平面.
故上述所作点为使得平面的点.
如图
在梯形中，有，
令，
因为，，三点共线，所以，.
即，所以，.
因为，所以，.
(3)设，
因为四点共面，所以存在实数，，使得.
因为，
，
又，，为一组基底，
所以
解得.
所以.
因为平面，平面，所以.
又，，在平面内，且相交于点，
所以平面，又平面，所以.
在四边形中，，，，
因为，点到的距离为，点到的距离为.
所以截面的面积.