初中数学人教版八年级上册12.2 三角形全等的判定学案设计

这是一份初中数学人教版八年级上册12.2 三角形全等的判定学案设计，共6页。学案主要包含了巩固训练，错题再现，精练反馈等内容，欢迎下载使用。

班级： 姓名： 组号：
一、巩固训练
1．下列关于直角三角形全等的判定，不正确的是（ ）
A．两条直角边对应相等。 B．斜边和一锐角对应相等。
C．斜边和一条直角边对应相等。 D．两锐角相等。
2．下列各条件中，不能作出唯一确定的三角形的是（ ）
A．已知两边和夹角 B．已知两角和夹边
C．已知两边和其中一边的对角 D．已知三边
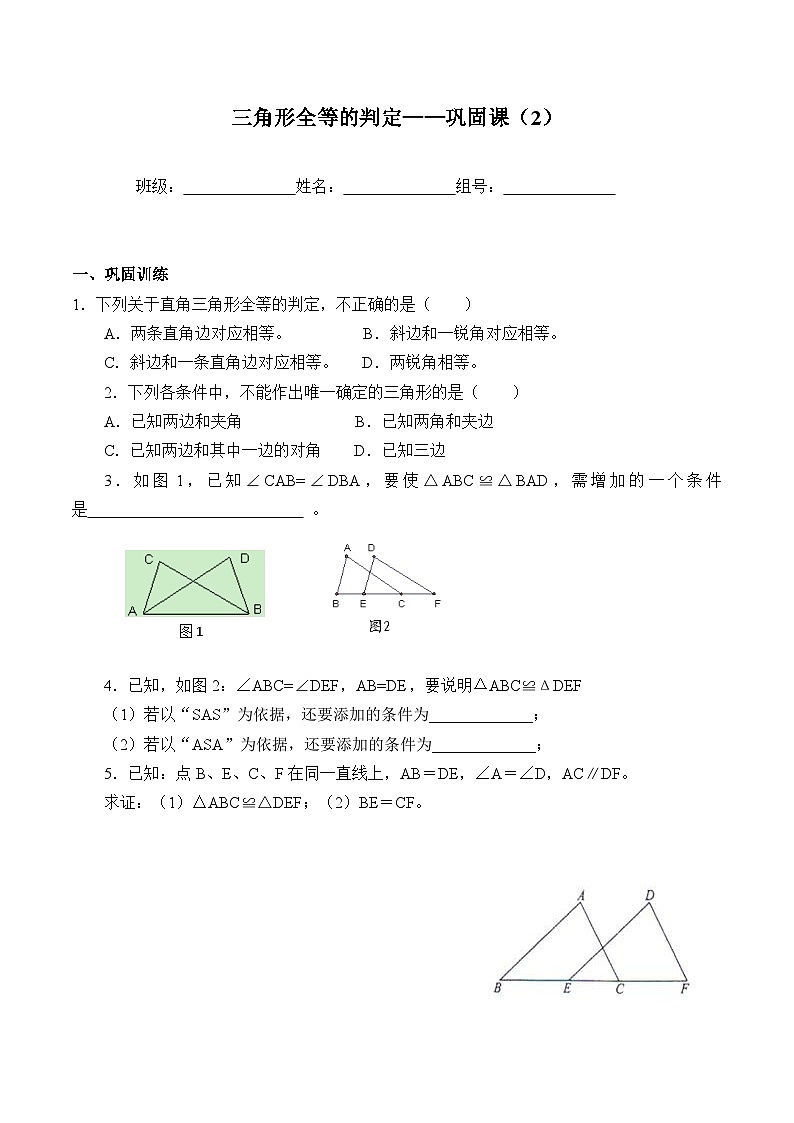
3．如图1，已知∠CAB=∠DBA，要使△ABC≌△BAD，需增加的一个条件是 。
图1
4．已知，如图2：∠ABC=∠DEF，AB=DE，要说明ΔABC≌ΔDEF
（1）若以“SAS”为依据，还要添加的条件为_____________；
（2）若以“ASA”为依据，还要添加的条件为_____________；
5．已知：点B、E、C、F在同一直线上，AB＝DE，∠A＝∠D，AC∥DF。
求证：（1）△ABC≌△DEF；（2）BE＝CF。
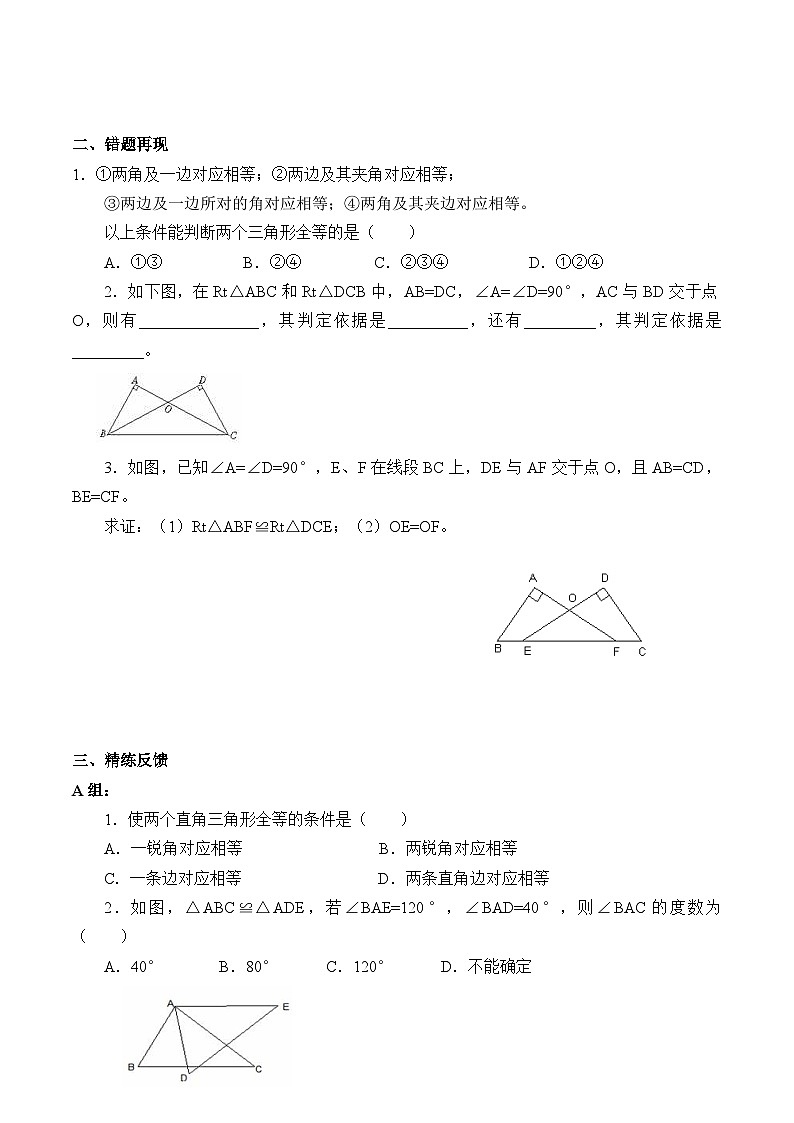
二、错题再现
1．①两角及一边对应相等；②两边及其夹角对应相等；
③两边及一边所对的角对应相等；④两角及其夹边对应相等。
以上条件能判断两个三角形全等的是（ ）
A．①③ B．②④ C．②③④ D．①②④
2．如下图，在Rt△ABC和Rt△DCB中，AB=DC，∠A=∠D=90°，AC与BD交于点O，则有_______________，其判定依据是__________，还有_________，其判定依据是_________。
3．如图，已知∠A=∠D=90°，E、F在线段BC上，DE与AF交于点O，且AB=CD，BE=CF。
求证：（1）Rt△ABF≌Rt△DCE；（2）OE=OF。

三、精练反馈
A组：
1．使两个直角三角形全等的条件是（ ）
A．一锐角对应相等 B．两锐角对应相等
C．一条边对应相等 D．两条直角边对应相等
2．如图，△ABC≌△ADE，若∠BAE=120°，∠BAD=40°，则∠BAC的度数为（ ）
A．40° B．80° C．120° D．不能确定
3．如图，已知AB=AD，AC=AE，∠1=∠2，求证：△ABC≌△ADE。
B组：
4．（1）如图，在正方形ABCD中E，F分别在边BC，CD上，AE，BF交于点O，∠AOF＝90°。求证：BE＝CF。
（2）如图在正方形ABCD中E、H、F、G分别在边AB，BC，CD，DA上，EF，GH交于点O，∠FOH＝90°，EF＝4。求GH的长。
（3）已知点E、H、F、G分别在矩形ABCD的边AB、BC、CD、DA上，EF、GH交于点O，∠FOH＝90°，EF＝4。直接写出下列两题的答案：
①如图矩形ABCD由2个全等的正方形组成，求GH的长______________；
②如图矩形ABCD由n个全等的正方形组成，求GH的长(用n的代数式表示)______________。
【答案】
巩固训练
1．D
2．C
3．∠C=∠D
4．（1）BC=EF （2）∠A=∠D
5．证明：（1）∵AC∥DF ∴∠ACB=∠EDF
在△ABC和△DEF中
∴△ABC≌△DEF（AAS）
（2）∵△ABC≌△DEF
∴BC=EF
∴BC－EC=EF－EC
∴BE=CF
错题再现
1．D
2．Rt△ABC≌Rt△DCB HL △ABO≌△DCO AAS
3．证明：（1）∵BE=CF ∴BE+EF=CF+EF ∴BF=CE
∴在Rt△ABF和Rt△DCE中
AB=CD BF=CE
∴Rt△ABF≌Rt△DCE
（2）∵Rt△ABF≌Rt△DCE
∴∠OEF=∠OFE
∴OF=OF
精练反馈
1．D 2．B
3．证明：∵∠1=∠2
∴∠1+∠BAE=∠2+∠BAE
∴∠DAE=∠BAC
在△ABC和△ADE中
∴△ABC≌△ADE（SAS）
4．（1）证明：
∵ABCD为正方形
∴∠C=∠ABC=∠D=90° AD∥BC AB=BC
∵∠AOF＝90°
∴∠AOF+∠D=180° ∴∠DFO+∠DAO=180°
∵∠DFO+∠CFB=180° ∴∠CFB=∠DAO
∵AD∥BC ∴∠DAO=∠AEB ∴∠CFB=∠AEB
∴△ABE≌△BCF ∴BE＝CF
（2）解：过点F作FM⊥AB于M，过点G作GN⊥BC于N，设GN、EF交点为P，
∵四边形ABCD是正方形，
∴GN=FM，且GN⊥FM，
∴∠EFM+∠GPF=90°，
∵∠FOH=90°，
∴∠HGN+∠GPF=90°，∴∠EFM=∠HGN，在△EFM和△HGN中，
∴△EFM≌△HGN（ASA），∴GH=EF，∵EF=4，∴GH=4
（3）①8 ②4n