2024版新教材高中数学第五章三角函数5.1任意角和蝗制5.1.1任意角课件新人教A版必修第一册

这是一份2024版新教材高中数学第五章三角函数5.1任意角和蝗制5.1.1任意角课件新人教A版必修第一册，共38页。

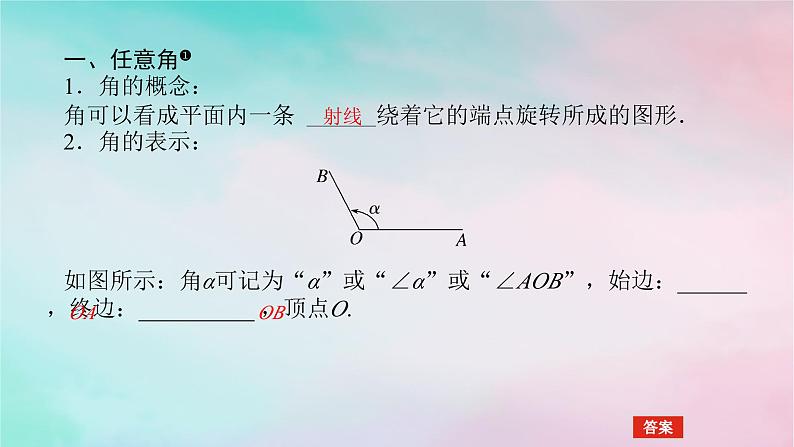
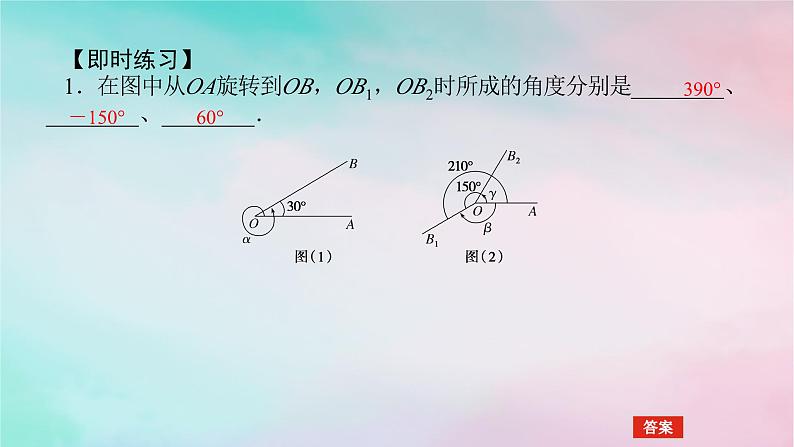
5.1.1　任意角预学案共学案预学案一、任意角❶1．角的概念：角可以看成平面内一条 ______绕着它的端点旋转所成的图形．2．角的表示：如图所示：角α可记为“α”或“∠α”或“∠AOB”，始边：______，终边：__________ ，顶点O.射线OAOB3．角的分类：逆时针顺时针没有4.角的加法与减法(1)如果角α和角β的旋转方向相同且旋转量相等，那么就称________．(2)设α，β是任意两个角，把角α的终边旋转角β，这时终边所对应的角是________．(3)相反角：把射线OA绕端点O按不同方向旋转相同的量所成的两个角叫做互为相反角，角α的相反角记为－α，于是有α－β＝________ .α＝βα＋βα＋(－β)【即时练习】　1．在图中从OA旋转到OB，OB1，OB2时所成的角度分别是________、________、________．390°－150°60°2．将一条射线绕着其端点顺时针旋转150°，再逆时针旋转90°，最后形成的角的度数为________．－60°解析：∵顺时针旋转所成的角为负角，逆时针旋转所成的角为正角，∴经两次旋转后形成的角的度数为－150°＋90°＝－60°.微点拨❶(1)正角、负角的引入是从正数、负数类比而来的，它们是用来表示具有相反意义的旋转量的．(2)在判断角度时，应时刻抓住“旋转”二字：①要明确旋转方向；②要明确旋转角的大小；③要明确射线的起始位置；④要注意由旋转方向来确定角的符号．(3)高中阶段所说的角实际上是初中所学概念“由一点出发的两条射线组成的图形叫做角”的推广．角的概念推广后，角度的范围不再限于0°～360°.(本书中，角α在0°～360°范围内是指0°≤α<360°)(4)零角的始边与终边重合．如果α是零角，那么α＝0°.二、象限角与终边相同的角❷1．象限角把角放在平面直角坐标系中，使角的顶点与原点重合，角的始边与______________重合，那么角的终边在第几象限，就说这个角是第几象限角；如果角的终边在________，就认为这个角不属于任何一个象限．2．终边相同的角所有与角α终边相同的角，连同角α在内，可构成一个集合S＝_____________________，即任一与角α终边相同的角，都可以表示成角α与整数个周角的和．x轴的非负半轴坐标轴上{β|β＝α＋k·360°，k∈Z}【即时练习】　1．判断正误(正确的画“√”，错误的画“×”)(1)第一象限角都是锐角．(　　)(2)第二象限角是钝角．(　　)(3)终边相同的角有无数个，它们相差360°的整数倍．(　　)××√2．下列选项中，与角α＝－30°终边相同的角是(　　)A．30° B．240°C．300° D．330°答案：D解析：与角α＝－30°终边相同的角表示为θ＝－30°＋360°·k，k∈Z，当k＝1时θ＝330°，故330°与角α＝－30°终边相同．故选D.3．－1 060°的终边落在(　　)A．第一象限 B．第二象限C．第三象限 D．第四象限答案：A解析：因为－1 060°＝－3×360°＋20°，所以－1 060°的终边与20°的终边相同，故落在第一象限．故选A.微点拨❷(1)角α为任意角，“k∈Z”不能省略．k有三层含义：①特殊性：对k每赋一个整数值就有一个具体对应的角．②一般性：表示所有与角α终边相同的角(包括α自身)．③从几何意义上看，k表示角的终边按一定的方向转动的圈数．k取正整数时，逆时针转动；k取负整数时，顺时针转动；k＝0时，没有转动．(2)k·360°与α中间要用“＋”连接，k·360°－α可理解成k·360°＋(－α)．(3)当角的始边相同时：相等的角的终边一定相同，而终边相同的角不一定相等；终边相同的角有无数个，它们相差360°的整数倍；终边不同则表示的角一定不同．共学案【学习目标】　(1)理解任意角的概念，学会在平面内建立适当的坐标系来讨论任意角．(2)能在指定范围内，找到一个与已知角终边相同的角，并判定其为第几象限角．(3)能写出与任一已知角终边相同的角的集合．(4)熟练掌握象限角与轴线角的集合表示．(5)会写出某个区间上角的集合．题型 1 任意角的概念【问题探究1】　(1)回忆初中我们是如何定义一个角的？所学的角的范围是什么？(2)在跳水比赛中，运动员会做出“转体两周”“向前翻转两周半”等动作，做上述动作时，运动员转体多少度？转过的度数还能用0°到360°的角度表示吗？提示：(1)角可以看成一条射线绕着它的端点旋转所成的图形，角的范围是0°～360°.(2)“转体两周”指顺时针旋转720°或逆时针旋转720°.“向前翻转两周半”指顺时针或逆时针旋转900°，转的角度不能用0°到360°的角表示．例1　将表的分针拨慢30分钟，则这个过程中时针转过的角度是(　　)A．10°　 B．15°C．30°　 D．－30°答案：B 学霸笔记：处理任意角问题的两个关键点(1)定方向：明确该角是由顺时针方向还是逆时针方向旋转形成的，由逆时针方向旋转形成的角为正角，否则为负角．(2)定大小：根据旋转角度的绝对值确定角的大小．跟踪训练1　经过2个小时，钟表的时针和分针转过的角度分别是(　　)A．60°，720° B．－60°，－720°C．－30°，－360° D．－60°，720°答案：B 题型 2 象限角【问题探究2】　为了进一步研究角的需要，我们常在直角坐标系内讨论角，并使角的顶点与原点重合，角的始边与x轴的非负半轴重合，那么对一个任意角，角的终边可能落在哪些位置？提示：第一、第二、第三、第四象限或坐标轴上．例2　下列命题中正确的是(　　)A．第一象限角一定不是负角B．钝角一定是第二象限角C．小于90°的角一定是锐角D．第一象限角一定是锐角答案：B解析：对于A，令α＝－300°＝60°－360°，显然α是第一象限角，同时也是负角，故A错误；对于B，不妨设θ是钝角，则90°<θ<180°，所以θ一定是第二象限角，故B正确；对于C，令β＝－60°，显然β是小于90°的角，但不是锐角，故C错误；对于D，令α＝－300°＝60°－360°，显然α是第一象限角，但不是锐角，故D错误．故选B.学霸笔记正确理解象限角与锐角、直角、钝角、平角、周角等概念的关系，需要掌握判断结论正确与否的技巧，判断结论正确需要证明，而判断结论不正确只需要一个反例即可．跟踪训练2　给出四个命题：①－60°是第四象限角；②235°是第三象限角；③475°是第二象限角；④－315°是第一象限角．其中正确的有(　　)个．A．1 B．2C．3 D．4答案：D解析：对①：－60°是第四象限角，故①正确；对②：180°<235°<270°，故其为第三象限角，故②正确；对③：475°＝360°＋115°，115°是第二象限角，故475°是第二象限角，③正确；对④：－315°＝－360°＋45°，45°是第一象限角，故－315°是第一象限角，④正确．故正确的有4个．故选D.题型 3 终边相同的角【问题探究3】　在同一平面直角坐标系中画出以下几个角：30°，－30°，390°，－330°.我们发现30°，390°，－330°这三个角的终边都是同一条射线，它们的终边相同．你还能找出哪些以这一条射线为终边的角？与30°终边相同的角与30°有什么关系？与30°终边相同的角的集合如何表示？ 提示：与30°、390°、－330°终边相同的角还有750°，－690°等，这样的角有无数个，它们之间相差360°的整数倍，所有与30°角终边相同的角的集合为{α|α＝30°＋k·360°，k∈Z}．例3　已知α＝－1 845°，在与α终边相同的角中，求满足下列条件的角. (1)最小的正角；(2)最大的负角；(3)－360°～720°之间的角．解析：因为－1 845°＝－45°＋(－5)×360°，即－1 845°角与－45°角的终边相同，所以与角α终边相同的角的集合是{β|β＝－45°＋k·360°，k∈Z}，(1)最小的正角为315°.(2)最大的负角为－45°.(3)－360°～720°之间的角分别是－45°，315°，675°.题后师说在某个范围内找与已知角终边相同的角的步骤跟踪训练3　(1)下列各角中，与26°角终边相同的角为(　　)A．206° B．－334°C．116° D．－154°答案：B　解析：与26°角终边相同的角为θ＝360°·k＋26°，k∈Z，对选项A：取θ＝360°·k＋26°＝206°，k不是整数解，排除；对选项B：取θ＝360°·k＋26°＝－334°，k＝－1，正确；对选项C：取θ＝360°·k＋26°＝116°，k不是整数解，排除；对选项D：取θ＝360°·k＋26°＝－154°，k不是整数解，排除．故选B.(2)终边落在x轴上的角的集合为____________________．{β|β＝k·180°，k∈Z} 题型 4 区域角的表示例4　写出终边在下列各图所示阴影部分内的角α的集合．解析：先写出边界角，再按逆时针顺序写出区域角，则得①{α|30°＋k·360°≤α≤150°＋k·360°，k∈Z}．②{α|－210°＋k·360°<α<30°＋k·360°，k∈Z}．题后师说表示区域角的一般步骤跟踪训练4　表示顶点在原点，始边重合于x轴的正半轴、终边落在阴影部分内的角的集合(不包含边界)．解析：图(1)中，330°＝360°－30°，∴对应为k·360°－30°<θ