初中数学人教版七年级上册3.2 解一元一次方程（一）----合并同类项与移项多媒体教学课件ppt

这是一份初中数学人教版七年级上册3.2 解一元一次方程（一）----合并同类项与移项多媒体教学课件ppt，共28页。PPT课件主要包含了逐点学练，本节小结，作业提升，本节要点，学习流程，知识点，合并同类项，系数化为1，解x＝1等内容，欢迎下载使用。

解一元一次方程——合并同类项解一元一次方程——移项一元一次方程的实际应用
解一元一次方程——合并同类项
1. 合并同类项 解方程时，将等号同侧的含有未知数的项和常数项分别合并成一项的过程，叫做合并同类项.
2. 用合并同类项解一元一次方程的步骤第一步：合并同类项，即将等号同侧的含未知数的项、常数项分别合并，把方程转化为ax=b(a ≠ 0)的形式.
特别解读解方程中的合并同类项和整式加减中的合并同类项一样，都是系数的合并，目的是运用合并同类项，使方程变得更简单，为利用等式的性质2求出方程的解创造条件.
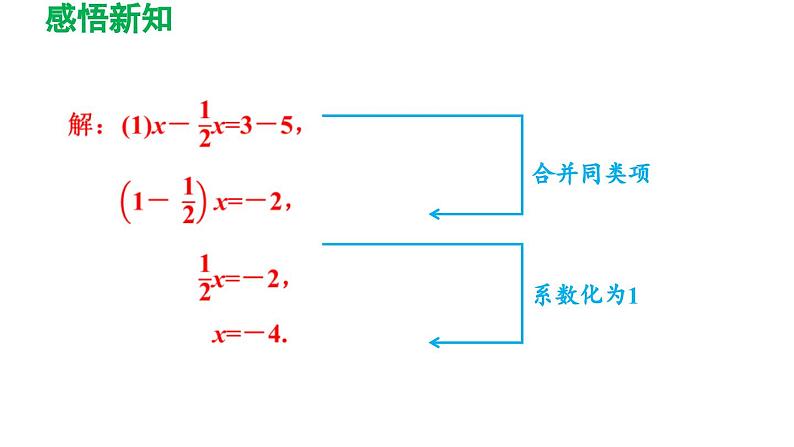
解题秘方：利用合并同类项的法则，将方程左右两边同时合并同类项，然后将未知数的系数化为1.
(2)－2x－7x+8x=－15×2－6×3， (－2－7+8)x=－48， －x=－48， x=48.
1-1. 解下列方程：(1)4x－3x=1 ；(2)－x+4x=6－1；
1. 移项 把等式一边的某项变号后移到另一边，叫做移项. 移项要变号.
解一元一次方程——移项
特别解读移项与加法交换律的区别：移项是在等式中，把某些项从等号的一边移到另一边，移动的项要变号；而加法交换律是交换加数的位置，只改变排列的顺序，不改变符号.
2. 移项的依据 移项的依据是等式的性质1，在方程的两边加(或减)同一个适当的整式，使含未知数的项集中在方程的一边，常数项集中在另一边.
解题秘方：利用移项解一元一次方程的步骤进行解答.
2-1. 解下列方程：(1)2x－3=x；(2)5x－2=7x+8；
解：2x－x＝ 3 x＝ 3
5x－7x＝ 8＋2 －2x＝ 10 x＝ －5
1. 列一元一次方程解决实际问题的一般步骤(1)审题，设未知数；(2)找相等关系，列方程；(3)解方程；(4)检验；(5)写出答案.
一元一次方程的实际应用
既要检验是否为方程的解，又要检验是否符合实际意义.
特别解读列一元一次方程解决实际问题时需要注意以下几点：1. 恰当地设未知数可以简化运算，且单位要统一；2. 题中的相等关系不一定只有一个，要根据具体情况选择；3. 求出方程的解后要检验.
2. 常见的两种基本相等关系(1)总量与分量关系问题：总量= 各分量的和；(2)余缺问题：表示同一个量的两个不同的式子相等.
利用方程解答下列问题：(1)x 的3 倍与2 的和等于x 的2 倍与1 的差，求x 的值；(2)已知整式－3x+2 与2x－1 的值互为相反数，求x 的值.
解题秘方：直接根据文字中揭示的相等关系列出方程，求出未知数的值.
解：(1)根据题意，得3x+2=2x－1.移项，得3x－2x=－1－2. 合并同类项，得x=－3.(2)根据题意，得－3x+2+2x－1=0，移项，得－3x+2x=－2+1，合并同类项，得－x=－1，系数化为1，得x=1.
未知数系数为－1时，方程还没有解完！
3-1. 已知式子3－4y 与2y－3 的和为－1， 求y的值.
某校七年级200 名学生分别到甲、乙两个纪念馆参观，其中到甲纪念馆参观的学生人数比到乙纪念馆参观的学生人数的2 倍少10 名，求到乙纪念馆参观的学生有多少名.
解题秘方：用分量的和等于总量列出方程，解决问题.
解：设到乙纪念馆参观的学生有x 名，则到甲纪念馆参观的学生有(2x－10)名. 根据题意，可得2x－10+x=200.解得x=70.答：到乙纪念馆参观的学生有70 名.
4-1. 某厂1 月份的产量为a 吨，2 月份的产量比1 月份增加了2 倍，3 月份的产量比2 月份增加了1 倍，如果第一季度的产量为1 800 吨，求1 月份的产量是多少.
解：由题意，得1月份的产量为a吨，2月份的产量为a＋2a＝3a(吨)，3月份的产量为2×3a＝6a(吨)，所以a＋3a＋6a＝1 800.合并同类项，得10a＝1 800.系数化为1，得a＝180.答：1月份的产量为180吨．
在国庆节来临之际，七年级(1)班课外活动小组计划做一批中国结. 如果每人做6 个，那么比计划多做7 个；如果每人做5 个，那么比计划少做13 个. 该小组计划做多少个中国结？
解题秘方：不管是余还是缺，总量不变是列方程的关键.
解：设该小组共有x 人，根据题意列方程，得6x－7=5x+13.解得x=20. 所以6x－7=113.答：该小组计划做113 个中国结.
5-1. 《九章算术》中有“盈不足术”的问题，原文如下：“今有共买羊，人出五，不足四十五；人出七， 不足三. 问：人数、羊价各几何？”题意是：若干人共同出资买羊，每人出5 钱，则差45 钱，每人出7 钱，则差3 钱，求人数和羊价各是多少.
解：设共有x人出资买羊，由题意，得5x＋45＝7x＋3.移项，得5x－7x＝3－45.合并同类项，得－2x＝－42.系数化为1，得x＝21.所以5x＋45＝5×21＋45＝150.答：共有21人出资买羊，羊价为150钱．
一个三角形的三边长之比为2∶4∶5，周长为22 cm，求该三角形最长边的长.
解题秘方：未知的量若以比例的形式出现，则解决问题的关键是求出单位量，通过设单位量表示总量列方程.
解：依题意，设该三角形的三边长分别为2x cm，4x cm，5x cm.根据题意，得2x+4x+5x=22，解得x=2.所以5x=10.答：该三角形最长边的长是10 cm.
(1)这个信息小组有多少人？
(2)七年级共有多少名同学？
解：设七年级共有y名同学．则50 ∶y＝2 ∶43，解得y＝1 075.答：七年级共有 1 075名同学．
一个两位数，十位上的数字是个位上的数字的2 倍，如果把个位上的数字与十位上的数字对调，得到的数比原数小36，求原来的两位数.
解题秘方：用各数位上的数字表示原数和新数，利用两个数之间的关系列方程.
解：设原来的两位数个位上的数字为x，则十位上的数字为2x. 根据题意，得10×2x+x－36=10x+2x，即20x+x－36=10x+2x.解得x=4.所以2x=8.答：原来的两位数是84.
教你一招：巧设元解数字问题的方法解决数字问题的关键在于如何巧妙地设出未知数，下面是一些数字问题设未知数的常用方法：(1)连续数设中间；(2)多位自然数设一位；(3)数字换位设部分；(4)小数点移动直接设；(5)数字成比例设比值；(6)特殊关系特殊设.
7-1. 下表是某年3月的月历：
(1)观察上面的月历，横行、竖列相邻的两数之间有什么关系？
解：横行相邻的两数相差1，竖列相邻的两数相差7.
(2)如果告诉你一竖列相邻三个数的和为72，你能知道这三天分别是几号吗？
解：设一竖列相邻三个数中中间的一个数为x，则上面的一个数为x－7，下面的一个数为x＋7.根据题意，得(x－7)＋x＋(x＋7)＝72.解这个方程，得x＝24.所以x－7＝24－7＝17，x＋7＝24＋7＝31.答：这三天分别是17号、24号、31号．
(3)如果用一个框圈出的2×2 个数的和为56，你知道圈出的四天分别是几号吗？
解：设圈出的四个数中，最小的数为y，则另外三个数分别为y＋1，y＋7，y＋8，根据题意，得y＋(y＋1)＋(y＋7)＋(y＋8)＝56.解这个方程，得y＝10.所以y＋1＝10＋1＝11，y＋7＝10＋7＝17，y＋8＝10＋8＝18.答：圈出的四天分别是10号、11号、17号、18号．
解一元一次方程（一）——合并同类项与移项