人教版九年级上册22.3 实际问题与二次函数精品同步练习题

这是一份人教版九年级上册22.3 实际问题与二次函数精品同步练习题，共46页。试卷主要包含了单选题，解答题等内容，欢迎下载使用。
第14课实际问题与二次函数
学校:___________姓名：___________班级：___________考号：___________

一、单选题
1．如图，一边靠墙（墙有足够长），其它三边用12m长的篱笆围成一个矩形（ABCD）花园，这个花园的最大面积是（     ）

A．18m2 B．12 m2 C．16 m2 D．22 m2
2．如图，四边形中，，若，则四边形的面积最大值为（ ）

A．6 B．18 C．36 D．144
3．某公司销售一种藜麦，成本价为30元/千克，若以35元/千克的价格销售，每天可售出450千克．当售价每涨0.5元/千克时，日销售量就会减少15千克．设当日销售单价为（元/千克）（，且是按0.5的倍数上涨），当日销售量为（千克）．有下列说法：
①当时，
②与之间的函数关系式为
③若使日销售利润为2880元，且销售量较大，则日销售单价应定为42元/千克
④若使日销售利润最大，销售价格应定为40元/千克
其中正确的是（    ）
A．①② B．①②④ C．①②③ D．②④
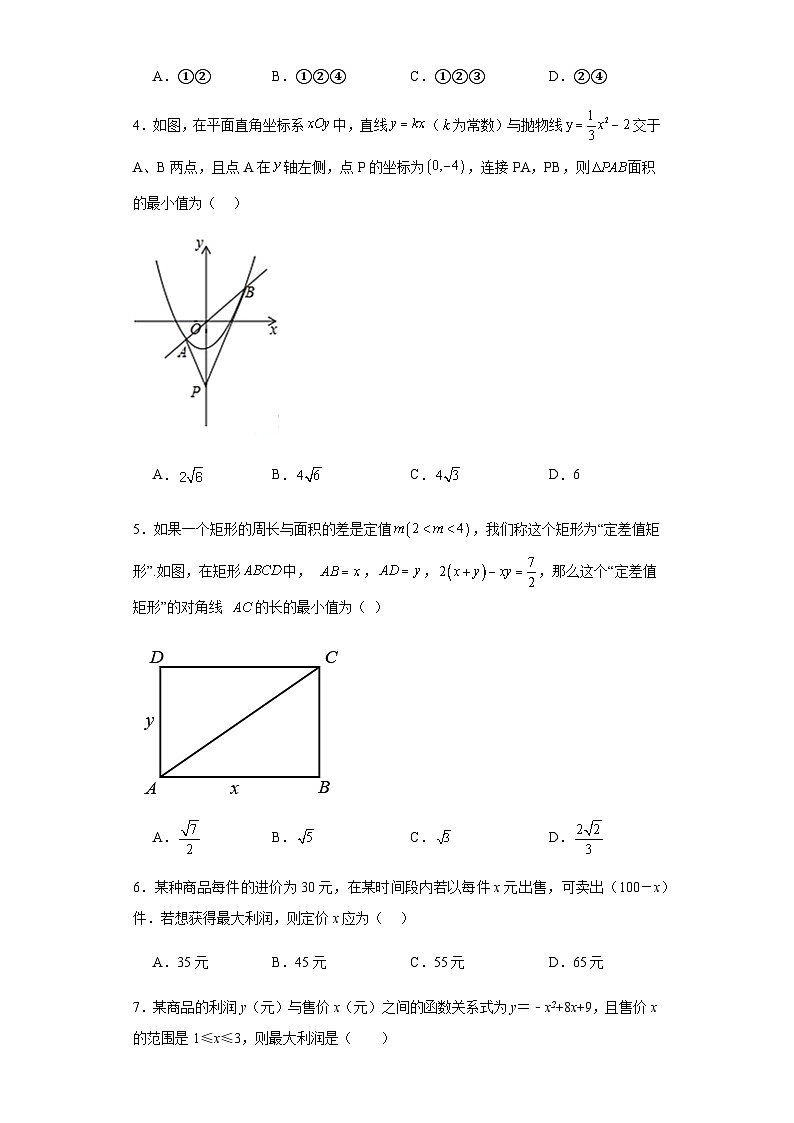
4．如图，在平面直角坐标系中，直线（为常数）与抛物线交于A、B两点，且点A在轴左侧，点P的坐标为，连接PA，PB，则面积的最小值为（    ）

A． B． C． D．6
5．如果一个矩形的周长与面积的差是定值，我们称这个矩形为“定差值矩形”.如图，在矩形中， ，，，那么这个“定差值矩形”的对角线 的长的最小值为（ ）

A． B． C． D．
6．某种商品每件的进价为30元，在某时间段内若以每件x元出售，可卖出（100－x）件．若想获得最大利润，则定价x应为（    ）
A．35元 B．45元 C．55元 D．65元
7．某商品的利润y（元）与售价x（元）之间的函数关系式为y＝﹣x2+8x+9，且售价x的范围是1≤x≤3，则最大利润是（　　）
A．16元 B．21元 C．24元 D．25元
8．某商场销售一批衬衫，平均每天可售出20件，每件盈利40元，经过调查发现，销售单价每降低5元，每天可多售出10件，下列说法错误的是（    ）
A．销售单价降低15元时，每天获得利润最大
B．每天的最大利润为1250元
C．若销售单价降低10元，每天的利润为1200元
D．若每天的利润为1050元，则销售单价一定降低了5元
9．如图，某涵洞的截面是抛物线形，现测得水面宽AB＝1.6m，涵洞顶点O与水面的距离CO是2m，则当水位上升1.5m时，水面的宽度为（    ）

A．0.4m B．0.6m C．0.8m D．1m
10．如图是抛物线形的拱桥，当水面宽4m时，顶点离水面2m，当水面宽度增加到6m时，水面下降（　　）

A．1m B．1.5m C．2.5m D．2m
11．从某幢建筑物2.25米高处的窗口A用水管向外喷水，水流呈抛物线，如果抛物线的最高点M离墙1米，离地面3米，那么水流落点B与墙的距离OB是（    ）

A．1米 B．2米 C．3米 D．4米
12．如图，要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管的长为（     ）

A． B． C． D．
13．一小球被抛出后，距离地面的高度h（米）和飞行时间t（秒）满足下面函数关系式：h =﹣5t2+20t﹣14，则小球距离地面的最大高度是（    ）
A．2米 B．5米 C．6米 D．14米
14．在地球上同一地点，不同质量的物体从同一高度同时下落，如果除地球引力外不考虑其他外力的作用，那么它们的落地时间相同．物体的下落距离h（m）与下落时间t（s）之间的函数表达式为h＝gt2．其中g取值为9.8m/s2．小莉进行自由落体实验，她从某建筑物抛下一个小球，经过4s后落地，则该建筑物的高度约为（   ）
A．98m B．78.4m C．49m D．36.2m
15．某种花卉每盆的盈利与每盆的株数有一定的关系，每盆植3株时，平均每株盈利4元．若每盆增加1株，平均每株盈利减少0.5元，要使每盆的盈利达到15元，每盆应多植多少株？设每盆多植x株，则可以列出的方程是（　　）
A．（3+x）（4﹣0.5x）＝15 B．（x+3）（4+0.5x）＝15
C．（x+4）（3﹣0.5x）＝15 D．（x+1）（4﹣0.5x）＝15
16．如图，用绳子围成周长为的矩形，记矩形的一边长为，矩形的面积为．当x在一定范围内变化时，S随x的变化而变化，则S与x满足的函数表达式为（    ）

A． B．
C． D．
17．某单车公司第一个月投放a辆单车，计划第三个月投放单车y辆，该公司第二、三两个月投放单车数量的月平均增长率为x，那么y与x的函数关系是（    ）
A． B． C． D．
18．向空中发射一枚炮弹，第x秒时的高度为y米，且高度与时间的关系为y＝ax2+bx+c（a≠0）．若此炮弹在第6秒与第18秒时的高度相等，则在下列时间中炮弹所在高度最高的是（　　）
A．第8秒 B．第10秒 C．第12秒 D．第15秒
19．如图是拱形大桥的示意图，桥拱与桥面的交点为O，B，以点O为原点，水平直线OB为x轴，建立平面直角坐标系，桥的拱形可以近似看成抛物线y=-0.01（x-20）2+4，桥拱与桥墩AC的交点C恰好位于水面，且AC⊥x轴，若OA=5米，则桥面离水面的高度AC为（  ）

A．米 B．米 C．米 D．米
20．如图，一个移动喷灌架喷射出的水流可以近似地看成抛物线，喷水头的高度（即的长度）是1米．当喷射出的水流距离喷水头8米时，达到最大高度1.8米，水流喷射的最远水平距离是（    ）

A．20米 B．18米 C．10米 D．8米
21．飞机着陆后滑行的距离s（单位：米）关于滑行时间t（单位：秒）的函数表达式为，当滑行时间为10秒时，滑行距离为450米；当滑行时间为20秒时，滑行距离为600米，则飞机的最大滑行距离为（    ）
A．600米 B．800米 C．1000米 D．1200米
22．使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m3）与旋钮的旋转角度x（单位：度）（0＜x≤90）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为（    ）

A．37.5° B．40°
C．42.5° D．45°
23．如图，四边形是边长为2的正方形，点是射线上的动点（点不与点，点重合），点在线段的延长线上，且,连接,．设，的面积为，下列图象能正确反映出与的函数关系的是（    ）

A． B．
C． D．
24．某超市销售一种商品，每件成本为元，销售人员经调查发现，该商品每月的销售量（件）与销售单价（元）之间满足函数关系式，若要求销售单价不得低于成本，为每月所获利润最大，该商品销售单价应定为多少元？每月最大利润是多少？（    ）
A．元，元 B．元，元
C．元，元 D．元，元
25．两个正方形的周长和是10，如果其中一个正方形的边长为，则这两个正方形的面积的和S关于的函数关系式为（    ）
A． B．
C． D．
26．某种产品按质量分为个档次，生产最低档次产品，每件获利润元，每提高一个档次，每件产品利润增加元，用同样工时，最低档次产品每天可生产件，提高一个档次将减少件．如果用相同的工时生产，总获利润最大的产品是第档次（最低档次为第一档次，档次依次随质量增加），那么等于（   ）
A． B． C． D．
27．如图，在边长为4的正方形ABCD中，动点P从A点出发，以每秒1个单位长度的速度沿AB向B点运动，同时动点Q从B点出发，以每秒2个单位长度的速度沿BC→CD方向运动，当P运动到B点时，P、Q两点同时停止运动．设P点运动的时间为t，△APQ的面积为S，则S与t的函数关系的图象是（）

A． B． C． D．
28．足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线，不考虑空气阻力，足球距离地面的高度h（单位：m）与足球被踢出后经过的时间t（单位：s）之间的关系如表：下列结论不正确的是（   ）
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
A．足球距离地面的最大高度超过20m B．足球飞行路线的对称轴是直线
C．点（10，0）在该抛物线上 D．足球被踢出时，距离地面的高度逐渐下降．
29．2020年6月中旬以来，北京市新冠肺炎疫情出现反弹，北京市民对防疫物资需求量激增．某厂商计划投资产销一种消毒液，设每天产销量为x瓶，每日产销这种消毒液的有关信息如下表：（产销量指生产并销售的数量，生产多少就销售多少，不考虑滞销和脱销）若该消毒液的单日产销利润y元，当销量x为多少时，该消毒液的单日产销利润最大．（    ）
消毒液
每瓶售价（元）
每瓶成本（元）
每日其他费用（元）
每日最大产销量（瓶）

30
18
1200＋0.02x2
250
A．250 B．300 C．200 D．550
30．如图，公园中一正方形水池中有一喷泉，喷出的水流呈抛物线状，测得喷出口高出水面0.8m，水流在离喷出口的水平距离1.25m处达到最高，密集的水滴在水面上形成了一个半径为3m的圆，考虑到出水口过高影响美观，水滴落水形成的圆半径过大容易造成水滴外溅到池外，现决定通过降低出水口的高度，使落水形成的圆半径为2.75m，则应把出水口的高度调节为高出水面（　　）

A．0.55米 B．米 C．米 D．0.4米

二、填空题
31．如图（1）是一个横断面为抛物线形状的拱桥，水面在l时，拱顶(拱桥洞的最高点)离水面3米，水面宽4米．如果按图（2）建立平面直角坐标系，那么抛物线的解析式是 ．

32．如图，若被击打的小球飞行高度h（单位：m）与飞行时间t（单位：s）之间具有的关系为h＝10t﹣5t2，则小球飞行的最大高度为 m．

33．某桥梁的桥洞可视为抛物线，，最高点C距离水面4m，以AB所在直线为x轴（向右为正向），若以A为原点建立坐标系时，该抛物线的表达式为，已知点D为抛物线上一点，位于点C右侧且距离水面3m，若以点D为原点，以平C行于AB的直线为x轴（向右为正向）建立坐标系时，该物线的表达式为 ．

34．如图，一名男生推铅球，铅球行进高度y（m）与水平距离x（m）之间的关系是y＝﹣，则他将铅球推出的距离是 m．

35．据了解，某蔬菜种植基地2019年的蔬菜产量为100万吨，2021年的蔬菜产量为万吨，如果2019年至2021年蔬菜产量的年平均增长率为，那么关于的函数解析式为 ．
36．如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称．AB//x轴，AB＝4cm，最低点C在x轴上，高CH＝1cm，BD＝2cm则右轮廓线DFE所在抛物线的函数表达式为 （不用写x的取值范围）．


37．某一型号飞机着陆后滑行的距离y（单位：m）与滑行时间x（单位：s）之间的函数表达式是，该型号飞机着陆后滑行的最大距离是 ．
38．如图所示，用长为21米的篱笆，一面利用墙（墙的最大可用长度a为10米），围成中间隔有一道篱笆的长方形花圃，为便于进出，开了3道宽为1米的门．设花圃的宽AB为x米，面积为S平方米，则S与x的之间的函数表达式为 ；自变量x的取值范围为 ．

39．某食品零售店新上架一款冷饮产品，每个成本为8元，在销售过程中，每天的销售量y（个）与销售价格x（元/个）的关系如图所示，当时，其图象是线段AB，则该食品零售店每天销售这款冷饮产品的最大利润为 元（利润=总销售额-总成本）．
  
40．如图①，“东方之门”通过简单的几何曲线处理，将传统文化与现代建筑融为一体，最大程度地传承了苏州的历史文化．如图②，“门”的内侧曲线呈抛物线形，已知其底部宽度为80米，高度为200米．则离地面150米处的水平宽度（即CD的长）为 ．


三、解答题
41．某商场经营一种新上市的文具，进价为20元，试营销阶段发现：当销售单价为25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件．
（1）若商场每天要获得销售利润2000元，销售单价应定为多少元？
（2）求销售单价定为多少元时，该文具每天的销售利润最大？最大利润为多少元？
42．为满足市场需求，某超市在中秋节前夕购进价格为12元/盒的某品牌月饼，根据市场预测，该品牌月饼每盒售价14元时，每天能售出200盒，并且售价每上涨1元，其销售量将减少10盒，为了维护消费者利益，物价部门规定：该品牌月饼的售价不能超过20元/盒．
(1)当销售单价为多少元时，该超市每天销售该品牌月饼的利润为720元；
(2)当销售单价为多少元时，超市每天销售该品牌月饼获得利润最大？最大利润是多少？
43．如图，ABCD是一块边长为4米的正方形苗圃，园林部门拟将其改造为矩形AEFG的形状，其中点E在AB边上，点G在AD的延长线上，DG = 2BE．设BE的长为x米，改造后苗圃AEFG的面积为y平方米．

（1）求y与x之间的函数关系式（不需写自变量的取值范围）；
（2）根据改造方案，改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等，请问此时BE的长为多少米？
44．小红看到一处喷水景观，喷出的水柱呈抛物线形状，她对此展开研究：测得喷水头P距地面0.7m，水柱在距喷水头P水平距离5m处达到最高，最高点距地面3.2m；建立如图所示的平面直角坐标系，并设抛物线的表达式为，其中x（m）是水柱距喷水头的水平距离，y（m）是水柱距地面的高度．

(1)求抛物线的表达式．
(2)爸爸站在水柱正下方，且距喷水头P水平距离3m，身高1.6m的小红在水柱下方走动，当她的头顶恰好接触到水柱时，求她与爸爸的水平距离．
45．一大型商场经营某种品牌商品，该商品的进价为每件6元，根据市场调查发现，该商品每周的销售量y（件）与售价x（元件）（x为正整数）之间满足一次函数关系，表格记录的是某三周的有关数据：
x（元/件）
7
8
9
y（件）
8500
8000
7500
(1)求y与x的函数关系式（不求自变量的取值范围）；
(2)在销售过程中要求销售单价不低于成本价，且不高于17元/件，若某一周该商品的销售最不少于6000件，求这一周该商场销售这种商品获得的最大利润和售价分别为多少元？
(3)抗疫期间，该商场这种商品售价不大于17元/件时，每销售一件商品便向某慈善机构捐赠m元（），捐赠后发现，该商场每周销售这种商品的利润仍随售价的增大而增大．请直接写出m的取值范围．
46．某工厂制作A、B两种手工艺品，B每件获利比A多105元，制作16件A与制作2件B获利相同．
(1)制作一件A和一件B分别获利多少元；
(2)工厂安排65人制作A，B两种手工艺品，每人每天制作2件A或1件B．现在在不增加工人的情况下，增加制作C工艺品．已知每人每天可制作1件C（每人每天只能制作一种手工艺品），要求每天制作A，C两种手工艺品的数量相等，设每天安排x人制作B，y人制作A．写出y与x之间的函数关系式；
(3)在（1）（2）的条件下，每天制作B不少于5件．当每天制作B为5件时，每件B获利不变，若B每增加1件，则当天平均每件B获利减少2元，已知C每件获利30元，求每天制作三种手工艺品可获得的总利润W（元）的最大值及相应x的值．

参考答案：
1．A
【解析】根据题意可以列出相应的函数关系式，然后化为顶点式即可解答本题．
【详解】解：设与墙垂直的矩形的边长为xm，
则这个花园的面积是：S=x（12-2x）=，
∴当x=3时，S取得最大值，此时S=18，
故选：A．
【点睛】本题考查二次函数的应用，解答本题的关键是明确题意，列出相应的函数关系式，利用二次函数的性质解答．
2．B
【分析】设，，根据题意表示四边形的面积，根据二次根式的性质作答即可．
【详解】如图，设AC、BD交于点M

设


四边形的面积即四边形的面积
当时，四边形的面积最大，最大为18．
故选：B．
【点睛】本题考查了二次函数的性质与最值问题、四边形的面积，熟练掌握知识点是解题的关键．
3．B
【分析】根据题意求出二次函数的解析式，再根据利润的关系逐一判断即可；
【详解】当时，，故①正确；
由题意得：，故②正确；
日销售利润为，
由题意得：，
整理得：，
解得：，，
∵销售单价为38元/千克时的销售量比销售单价为42元/千克时大，
∴不合题意，
即若使日销售利润为2880元，且销售量较大，则日销售单价应定为38元/千克，故③错误；
由上问可知：，
即，
∵，
∴当时，，
即若使日销售利润最大，销售价格应定为40元/千克，故④正确；
故正确的是①②④；
故答案选B．
【点睛】本题主要考查了二次函数的实际应用，准确计算是解题的关键．
4．B
【分析】设，首先联立抛物线与直线的解析式，得出关于A，B横坐标的应用二次方程，再利用根与系数的关系得出最后将所求三角形面积分割成两部分面积之和即可得出答案.
【详解】解：设，联立，得，即，
由根与系数的关系得
，
∴当时，的面积最小，最小面积为.
故选：B.
【点睛】本题考查的知识点是直线与抛物线的交点问题，具有一定难度. 选错的原因是：1.没有掌握二次函数与直线相交求交点坐标的方法；2.没有掌握根与系数的关系；3.未能将所求三角形面积分割成两部分面积之和.
5．C
【分析】根据矩形的性质，由勾股定理可得，由二次函数的性质可求解．
【详解】解：∵在矩形中，，，，
∴，
∴，
∵，
∴，
∴，
∴当时，，
∴有最小值为（取正值），
故选：C．
【点睛】本题考查了矩形的性质，勾股定理，二次函数的性质，掌握相关性质是本题的关键．
6．D
【分析】设所获得的利润为W，根据利润=（售价-进价）×数量，列出W关于x的二次函数，利用二次函数的性质求解即可．
【详解】解：设所获得的利润为W，
由题意得，
∵，
∴当时，W有最大值1225，
故选D．
【点睛】本题主要考查了二次函数的应用，解题的关键在于能够根据题意列出利润关于售价的二次函数．
7．C
【分析】把y=-x2+8x+9配方得到y=-（x-4）2+25，当x＜4时，y随x的增大而增大，于是求得当x=3时，最大利润y是24元．
【详解】解：y=-x2+8x+9=-（x-4）2+25，
∵a=-1＜0，
∴利润y有最大值，
当x＜4时，y随x的增大而增大，
∵售价x的范围是1≤x≤3，
∴当x=3时，最大利润y是24元，
故选：C．
【点睛】本题考查了二次函数的应用，二次函数的性质，熟练掌握二次函数的性质是解题的关键．
8．D
【分析】设每件降价x元，由“每降低5元，每天可多售出10件”可知每降价1元可多售2件，根据题意可知每天的利润为（20+2x）（40-x），据此一一判断选项即可.
【详解】因为每降低5元，每天可多售出10件，所以每降价1元可多售2件，
设每件降价x元，每天的利润为y元，则每天可售（20+2x）件，每件利润为40-x，
所以每天的利润为
将整理成顶点式有，
由顶点式可知当销售单价降低15元时，每天获得利润最大，每天的最大利润为1250元，故A、B正确；
将x=10代入到解析式中解得y=1200，故C正确；
令y=1050，则，解得，即当每天的利润为1050元，则销售单价可能降低了5元，也可能降低了25元，所以D错误；
综上所述，答案选D.
【点睛】本题考查的是二次函数的实际应用，能够根据题意列出每天利润与降低单价的二次函数方程是解题的关键.
9．C
【分析】根据题意可建立平面直角坐标系，然后设函数关系式为，由题意可知，代入求解函数解析式，进而问题可求解．
【详解】解：建立如图所示的坐标系：

设函数关系式为，由题意得：，
∴，
解得：，
∴，
当y=-0.5时，则有，
解得：，
∴水面的宽度为0.8m；
故选C．
【点睛】本题主要考查二次函数的应用，熟练掌握二次函数的应用是解题的关键．
10．C
【分析】根据已知得出直角坐标系，进而求出二次函数的解析式，再把代入抛物线的解析式得出水面宽度，即可得出答案．
【详解】解：建立平面直角坐标系，设横轴通过，纵轴通过中点且通过顶点，则通过画图可得知为原点，

由平面直角坐标系可知，，即，
设抛物线的解析式为，
将点代入得：，解得，
则抛物线的解析式为，即，
当时，，
所以水面下降，
故选：C．
【点睛】本题主要考查了二次函数的应用，根据已知建立平面直角坐标系从而得出二次函数的解析式是解决问题的关键．
11．C
【分析】根据题意可以求得抛物线的解析式，从而可以求得点B的坐标，本题得以解决．
【详解】解：由题意可得，抛物线的顶点坐标为（1，3），
设抛物线的解析式为：y=a（x-1）2+3，
2.25=a（0-1）2+3，
解得a=-0.75，
∴y=-（x-1）2+3，
当y=0时，-（x-1）2+3=0，
解得，x1=-1，x2=3，
∴点B的坐标为（3，0），
∴OB=3，
答：水流下落点B离墙距离OB的长度是3米．
故选：C．
【点睛】本题考查了二次函数的应用，解答本题的关键是明确题意，求出相应的函数解析式，利用二次函数的性质解答．
12．A
【分析】利用顶点式求得抛物线的解析式，再令x=0，求得相应的函数值，即为所求的答案．
【详解】解：由题意可知点（1，3）是抛物线的顶点，
∴设这段抛物线的解析式为y=a（x-1）2+3．
∵该抛物线过点（3，0），
∴0=a（3-1）2+3，
解得：a=-．
∴y=-（x-1）2+3．
∵当x=0时，y=-（0-1）2+3=-+3=，
∴水管应长m．
故选：A
【点睛】本题考查了二次函数在实际问题中的应用，数形结合并熟练掌握待定系数法及二次函数的相关性质是解题的关键．
13．C
【分析】首先理解题意，先把实际问题转化成数学问题后，知道解此题就是求出h =﹣5t2+20t﹣14的顶点纵坐标即可．
【详解】高度h和飞行时间t 满足函数关系式：h =﹣5t2+20t﹣14，
当时，小球距离地面高度最大，
米，
故选：C．
【点睛】本题考查的知识点是二次函数的应用，解题关键是把实际问题转化成数学问题，利用二次函数的性质就能求出结果．
14．B
【分析】把t=4代入h＝gt2可得答案．
【详解】解：把t=4代入h＝gt2得，

故选：B．
【点睛】本题考查二次函数的实际应用，根据题意把t=4代入是解题关键
15．A
【分析】根据已知假设每盆花苗增加x株，则每盆花苗有(x+3)株，得出平均单株盈利为(4-0.5x)元，由题意得(x+3)(4-0.5x)=15即可．
【详解】解：设每盆应该多植x株，由题意得
(x+3)(4-0.5x)=15，
故选：A．
【点睛】此题考查了一元二次方程的应用，根据每盆花苗株数×平均单株盈利=总盈利得出方程是解题关键．
16．A
【分析】矩形的周长为2（x+y）＝10，可用x来表示y，代入S＝xy中，化简即可得到S关于x的函数关系式．
【详解】解：由题意得，
2（x+y）＝10，
∴x+y＝5，
∴y＝5﹣x，
∵S＝xy
＝x（5﹣x）
∴矩形面积满足的函数关系为S＝x（5﹣x），
由题意可知自变量的取值范围为，
故选：A．
【点睛】本题考查了二次函数在实际问题中的应用，理清题中的数量关系并熟练掌握二次函数的解析式形式是解题的关键．
17．B
【分析】根据增长率的问题可直接进行求解．
【详解】解：由题意得：，
故选B．
【点睛】本题主要考查二次函数的应用，熟练掌握二次函数的应用是解题的关键．
18．C
【分析】先根据题意求出抛物线的对称轴，即可得出顶点的横坐标，从而得出炮弹所在高度最高时的值．
【详解】解：此炮弹在第6秒与第18秒时的高度相等，
抛物线的对称轴直线是：，
抛物线开口向下，
时，函数值最大，
即第12秒炮弹所在高度最高，
故选：C．
【点睛】本题主要考查了二次函数的应用，在解题时要能根据题意求出抛物线的对称轴得出答案是本题的关键．
19．C
【分析】根据OA=5知点C的横坐标为-5，据此求出点C的纵坐标即可得出答案．
【详解】解：∵AC⊥x轴，OA=5米，
∴点C的横坐标为-5，
当x=-5时，y=-0.01（x-20）2+4=y=-0.01（-5-20）2+4=-2.25，
∴C（-5，-2.25），
∴桥面离水面的高度AC为2.25米．
故选：C．
【点睛】本题考查了二次函数的应用．解题的关键是明确题意找出所求问题需要的条件．
20．A
【分析】根据顶点式求得抛物线解析式，进而求得与轴的交点坐标即可求解．
【详解】解：∵喷水头的高度（即的长度）是1米．当喷射出的水流距离喷水头8米时，达到最大高度1.8米，
设抛物线解析式为，将点代入，得

解得
∴抛物线解析式为
令，解得（负值舍去）
即，

故选：A
【点睛】本题考查了二次函数的实际应用，根据题意求得解析式是解题的关键．
21．A
【分析】先根据滑行时间为10秒时，滑行距离为450米；当滑行时间为20秒时，滑行距离为600米，求出函数的解析式，然后求出函数的最大值即可．
【详解】解：∵时，；时，，
∴，解得：，
∴，
∵，
∴当时，S最大，且最大值为600，
即飞机的最大滑行距离为600米，故A正确．
故选：A．
【点睛】本题主要考查了求二次函数解析式和最大值，根据题意求出二次函数解析式，是解题的关键．
22．B
【分析】根据题意和二次函数的性质，可以确定出对称直线x的取值范围，从而可以解答本题．
【详解】解：由图象可得，
该函数的对称轴x＞且x＜50，
∴37.5＜x＜50，即对称轴位于直线x＝37.5与直线x＝50之间且靠近直线x＝37.5
∴此燃气灶烧开壶水最节省燃气的旋钮角度约为40°，
故选：B．
【点睛】本题考查二次函数的应用，解答本题的关键是明确题意，利用数形结合的思想解答．
23．B
【分析】分两种情况进行讨论，当点在之间时，即，，
当点在上方时，即，，根据图象的开口方向的类项即可判断．
【详解】解：当点在之间时，即，
，则，
，
图象是开口向下，对称为：的抛物线，
当点在上方时，即，
，则，
，
图象是开口向上的抛物线，
故选：B．
【点睛】本题考查了二次函数的图象及性质，解题的关键是求出函数的解析式．
24．B
【分析】设每月所获利润为w，按照等量关系列出二次函数，并根据二次函数的性质求得最值即可．
【详解】解：设每月总利润为，
依题意得：



，此图象开口向下，又，
当时，有最大值，最大值为元．
故选：B．
【点睛】本题考查了二次函数在实际生活中的应用，根据题意找到等量关系并掌握二次函数求最值的方法是解题的关键．
25．D
【分析】依据正方形的面积公式即可求解．
【详解】∵两个正方形的周长和是10，如果其中一个正方形的边长为，
∴另一个正方形的边长为，
∴这两个正方形的面积的和S关于的函数关系式为，
故选：D．
【点睛】此题主要考查了根据实际问题列二次函数关系式，解决本题的难点是求得另一正方形的边长，根据题意，找到所求量的等量关系是解决问题的关键．
26．C
【分析】第档次产品比最低档次产品提高了个档次，则数量在60的基础上减少了，每件产品利润在8的基础上增加，据此可求出总利润关系，求出最值即可．
【详解】解：设总利润为y元，
∵第档次产品比最低档次产品提高了个档次，
∴每天利润为，
∴当时，产品利润最大，每天获利864元，
故选C．
【点睛】本题考查了二次函数的实际应用，借助二次函数解决实际问题是本题的关键．
27．D
【详解】∵动点Q从B点出发，以每秒2个单位长度的速度沿BC→CD方向运动，
∴点Q运动到点C的时间为4÷2=2秒．
由题意得，当0≤t≤2时，即点P在AB上，点Q在BC上，AP=t，BQ=2t，
，为开口向上的抛物线的一部分．
当2＜t≤4时，即点P在AB上，点Q在DC上，AP=t，AP上的高为4，
，为直线（一次函数）的一部分．
观察所给图象，符合条件的为选项D．故选D．
28．C
【分析】由题意，可得对称轴为，则可得抛物线经过（0，0），（9，0），所以可以假设抛物线的解析式为h＝at（t﹣9），把（1，8）代入可得a＝﹣1，可得，由此即可一一判断．
【详解】解：由题意，可得对称轴为，则可得抛物线经过（0，0），（9，0）
设抛物线的解析式为h＝at（t﹣9），把（1，8）代入可得a＝﹣1，
，
∴足球距离地面的最大高度为20.25m＞20m，A选项正确，不符合题意；
∴抛物线的对称轴，故B正确，不符合题意；
由二次函数的性质可得，当时，h随t的增大而减小，
∴足球被踢出时，距离地面的高度逐渐下降，D选项正确，不符合题意，
抛物线经过点（9，0），不经过（10，0），
∴点（10，0）不在该抛物线上，C选项错误，符合题意；
故选：C
【点睛】本题考查二次函数的应用，解答本题的关键是明确题意，求出相应的函数解析式，利用二次函数的性质解答．
29．D
【分析】根据单日利润=单日的销售量×每瓶的利润－每日其他费用即可列出函数关系式，然后利用函数的最值问题即可求解 ．
【详解】解：根据题意，得

∴，
∴，
∵，
∴抛物线的开口向下，有最大值，
又∵，
∴当时，，
故选：D
【点睛】本题考查了二次函数的应用，根据题意正确列出函数关系式是解题的关键．
30．B
【分析】如图，以O为原点，建立平面直角坐标系，由题意得到对称轴为x＝1.25＝，A（0，0.8），C（3，0），列方程组求得函数解析式，即可得到结论．
【详解】解：如图，以O为原点，建立平面直角坐标系，
由题意得，对称轴为x＝1.25＝，A（0，0.8），C（3，0），
设解析式为y＝ax2+bx+c，
∴，
解得：，
所以解析式为：y＝x2+x+，
当x＝2.75时，y＝，
∴使落水形成的圆半径为2.75m，则应把出水口的高度调节为高出水面08﹣＝，
故选：B．

【点睛】本题考查了二次函数的实际应用，根据题意建立合适的坐标系，找到点的坐标，用待定系数法解出函数解析式是解题的关键
31．
【分析】设出抛物线方程y=ax2（a≠0）代入坐标（-2，-3）求得a．
【详解】解：设出抛物线方程y=ax2（a≠0），由图象可知该图象经过（-2，-3）点，
∴-3=4a，
a=-，
∴抛物线解析式为y=-x2．
故答案为：．
【点睛】本题主要考查二次函数的应用，解题的关键在于能够熟练掌握待定系数法求解二次函数解析式．
32．5
【分析】将h＝10t﹣5t2化为顶点式即可求解．
【详解】解：∵，
∴小球飞行的最大高度为5m，
故答案为5．
【点睛】本题考查了二次函数的性质在实际生活中的应用．能将二次函数化为顶点式是解题的关键．
33．/
【分析】在y＝﹣x2+x中，令y＝3可得xD﹣xA＝9，以点D为原点，以平行于AB的直线为x轴（向右为正向）建立坐标系，根据题意知此时顶点D（﹣3，1），A（﹣9，﹣3），设抛物线的表达式为y＝a（x+3）2+1，将A（﹣9，﹣3）代入即得抛物线的表达式为y＝﹣（x+3）2+1＝﹣x2﹣x．
【详解】解：在y＝﹣x2+x中，令y＝3得﹣x2+x＝3，
解得x＝3或x＝9，
∵点D为抛物线上一点，位于点C右侧且距离水面3m，
∴xD﹣xA＝9，
以点D为原点，以平行于AB的直线为x轴（向右为正向）建立坐标系，如图：

根据题意知此时顶点D（﹣3，1），A（﹣9，﹣3），
设抛物线的表达式为y＝a（x+3）2+1，
将A（﹣9，﹣3）代入得：36a+1＝﹣3，
解得a＝﹣，
∴抛物线的表达式为y＝﹣（x+3）2+1＝﹣x2﹣x，
故答案为：y＝﹣x2﹣x．
【点睛】此题主要考查了二次函数的应用，求出A、C坐标，利用顶点式求函数解析式是解题关键．
34．10
【分析】成绩就是当高度y=0时x的值，所以解方程可求解．
【详解】解：当y=0时，-=0，
解之得x1=10，x2=-2（不合题意，舍去），
所以推铅球的距离是10米．
故答案为10
【点睛】此题把函数问题转化为方程问题来解，渗透了函数与方程相结合的解题思想方法．
35．
【分析】根据题意可得2020年的蔬菜产量为，2021年的蔬菜产量为，2021年的蔬菜产量为y万吨，由此即可得．
【详解】解：根据题意可得：2020年的蔬菜产量为，
2021年的蔬菜产量为，
∴，
故答案为： ．
【点睛】题目主要考查二次函数的应用，理解题意，熟练掌握增长率问题是解题关键．
36．
【分析】根据题意可以求得点C、点B的坐标，然后根据眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称，从而可以求得点D和点F的坐标，然后设出右轮廓线DFE所在抛物线的函数顶点式，从而可以解答本题．
【详解】解：∵眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称，AB∥x轴，AB＝4cm，最低点C在x轴上，高CH＝1cm，BD＝2cm，
∴点C的坐标为（﹣3，0），点B（﹣1，1），
∴点D（1，1），点F（3，0），
设右轮廓线DFE所在抛物线的函数解析式为：y＝a（x﹣3）2，
则1＝a（1﹣3）2，
解得，a＝，
∴右轮廓线DFE所在抛物线的函数解析式为：
【点睛】本题考查二次函数的应用，解答此类问题的关键是明确题意，求出抛物线的顶点坐标和经过的点D的坐标，利用二次函数的顶点式解答．
37．600m/600米
【分析】根据题意可以将y关于x的代数式化为顶点式，从而可以求得y的最大值，从而可以解答本题．
【详解】解：∵，
∴x=20时，y取得最大值，最大值=600，
故答案为：600m．
【点睛】本题考查二次函数的应用，解题的关键是明确题意，找出所求问题需要的条件．
38．
【分析】根据题意表示出长方形的长进而得出函数关系，进而结合a的最大值得出x的取值范围．
【详解】解：设花圃的宽AB为x米，面积为S平方米，
则S与x的之间的函数表达式为：；
由题意可得：，
解得：．
故答案为：，．
【点睛】本题主要考查根据实际问题列二次函数关系式，解决本题的关键是正确表示出长方形的长．
39．121
【分析】利用待定系数法求一次函数解析式，然后根据“利润=单价商品利润×销售量”列出二次函数关系式，从而根据二次函数的性质分析其最值．
【详解】解：当时，设，把（10，20），（20，10）代入可得：
，
解得，
∴每天的销售量y（个）与销售价格x（元/个）的函数解析式为，
设该食品零售店每天销售这款冷饮产品的利润为w元，
，
∵1