北师大版九年级上册3 用公式法求解一元二次方程教案配套课件ppt

这是一份北师大版九年级上册3 用公式法求解一元二次方程教案配套课件ppt，共17页。PPT课件主要包含了复习回顾，方案1，方案2，方案3，方案4，πx296，典例精析，随堂即练等内容，欢迎下载使用。

1.能够建立一元二次方程模型解决有关面积的问题.（重点、难点）2.能根据具体问题的实际意义检验结果的合理性.（难点）
1、怎样用配方法解一元二次方程？
用配方法解方程的步骤:
化：二次项系数化为 1 ；移：将常数项移到等号右边；配：配方，使等号左边成为完全平方式；开：等号两边开平方；解：求出方程的解。
2、怎样用公式法解一元二次方程？
对于一元二次方程 ax2 + bx + c = 0（a≠0），
当b2 - 4ac ≥ 0 时，它的根是：
用求根公式解一元二次方程的方法称为公式法.
问题：如图，某小区规划在一个长30 m、宽20 m的长方形土地上修建三条等宽的通道，使其中两条与AB平行，另外两条与AD平行，其余部分种花草，要使每一块花草的面积都为 78 m2，那么通道宽应该设计为多少？设通道宽为x m，则由题意列的方程为_____________________.
(30-2x)(20-x)=6×78
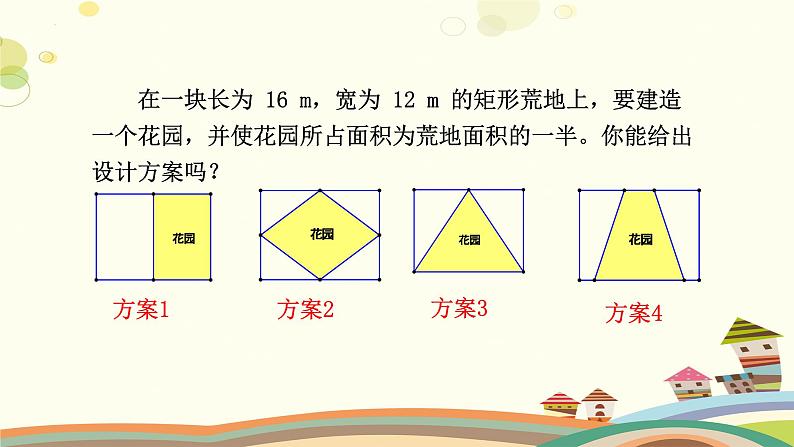
在一块长为 16 m，宽为 12 m 的矩形荒地上，要建造一个花园，并使花园所占面积为荒地面积的一半。你能给出设计方案吗？
解：设小路的宽为 x m, 根据题意，得 即 x2 - 14x + 24 = 0. 解得 x1 = 2 , x2 = 12. 将x =12 代入方程中不符合题意舍去. 答：小路的宽为2 m.
小明设计： 如图所示，其中花园四周小路的宽都相等.通过解方程, 得到小路的宽为2 m或12 m.
问题：你觉得他的结果对吗？你能将小明的解答过程重现吗？
小芳设计： 如图所示，其中花园每个角上的扇形都相同.
问题：你能帮小亮计算一下这个扇形的半径是多少吗？
解：设扇形的半径为x m，由题意得：
x1≈ 5.5，x2≈ -5.5（舍）
小华设计：如图所示，其中花园是两条互相垂直的小路,且它的宽都相等.
问题：你能帮小颖计算一下图中x吗？
解：设小路的宽为 x m. 根据题意，得即 x2 - 28x + 96 = 0.解得 x1 = 4 , x2 = 24,将x =24 代入方程中不符合题意，舍去.答：小路的宽为4 m.
例1.对于任意实数k，关于x 的方程x2－2(k+1)x－k2+2k－1=0的根的情况为( C )A. 有两个相等的实数根 B. 没有实数根C. 有两个不等的实数根 D. 无法判断
例2.将一根长为20 cm 的铁丝剪成两段，并以每一段铁丝的长度为周长做成正方形.(1)要使这两个正方形的面积之和等于17 cm2，那么这根铁丝剪成两段后的长度分别是多少？
(2)两个正方形的面积之和可能等于12 cm2 吗？若可能，分别求出两段铁丝的长度；若不可能，请说明理由.
1.关于x的一元二次方程x2－(k－3)x－k+1=0的根的情况，下列说法正确的是(　　)A. 有两个不相等的实数根 B. 有两个相等的实数根C. 无实数根 D. 无法确定
2. 某农场要建一个长方形的养鸡场,养鸡场的一边靠墙(墙长25 m),另外三边用木栏围成,木栏长40 m.
养鸡场的面积能达到180 m2 吗?如果能,请给出设计方案;如果不能,请说明理由.
3.如图,在一块长为 92 m ,宽为 60 m 的矩形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为 885 m2 的 6 个矩形小块,水渠应挖多宽？