





还剩12页未读,
继续阅读
2.5 逆命题和逆定理 浙教版数学八年级上册课件
展开
这是一份2.5 逆命题和逆定理 浙教版数学八年级上册课件,共20页。
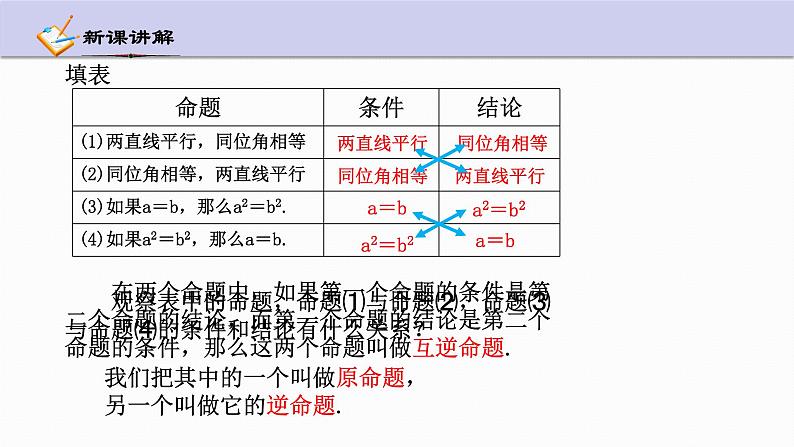
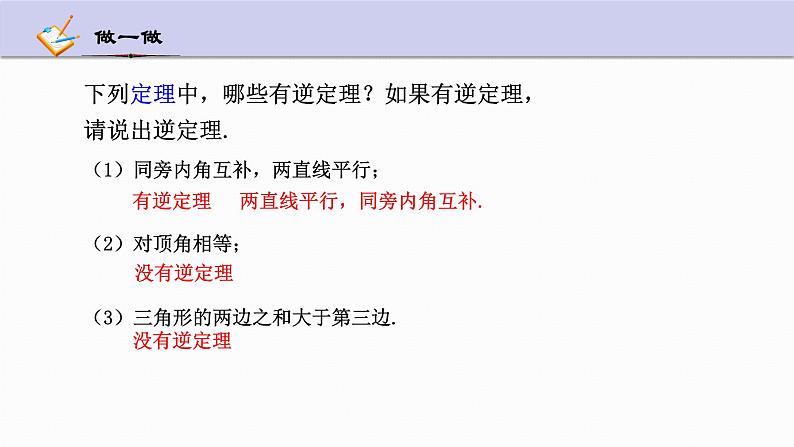
2.5 逆命题和逆定理浙教版《数学》八年级上册教学目标1.经历逆命题概念的发生过程,了解一个命题都是由条件与结论两部分构成,每个命题都有它的逆命题,命题由真假之分;2.了解逆命题、逆定理的概念.探索线段垂直平分线性质定理的逆定理,培养学生敢于面多挑战和勇于克服困难的意志.通过认识两个命题是不是逆命题,在简单情况下写出一个命题的逆命题,提高学生的表达能力和说理的条理性.1. 下列句子是命题的是 ( ) A.画∠AOB=45° B. 小于直角的角是锐角吗? C.连结CD D. 飞机是会飞的交通工具对某件事作出正确或不正确判断的句子叫做命题D命题由条件、结论组成正确的命题是真命题,错误的命题是假命题命题的定义:命题的结构:命题有真有假: 观察表中的命题,命题⑴与命题⑵,命题⑶与命题⑷的条件和结论有什么关系?a=ba2=b2a2=b2a=b两直线平行同位角相等同位角相等两直线平行填表 在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.我们把其中的一个叫做原命题,另一个叫做它的逆命题.说出下列命题的逆命题,并判定原命题和逆命题的真假:圆既是中心对称,又是轴对称的图形.平行四边形有一组对边平行且相等.高速行驶时不接触地面的交通工具是磁悬浮列车.(1)既是中心对称,又是轴对称的图形是圆.(2)有一组对边平行且相等的四边形是平行四边形.(3)磁悬浮列车是一种高速行驶时不接触地面的交通 工具.真命题假命题假命题真命题真命题真命题 如果一个定理的逆命题能被证明是真命题,那么就叫它是原定理的逆定理,这两个定理叫互逆定理.注:逆定理、互逆定理一定都是真命题.下列定理中,哪些有逆定理?如果有逆定理,请说出逆定理.(1)同旁内角互补,两直线平行;(2)对顶角相等;(3)三角形的两边之和大于第三边.没有逆定理两直线平行,同旁内角互补.没有逆定理有逆定理判断下列说法是否正确?请说明理由(1)假命题没有逆命题; (2)真命题没有逆命题; (3)每个命题都有逆命题; (4)真命题的逆命题是真命题; √×××(5)每个定理都有逆定理;×(6)逆定理有真有假.×例1 说出定理“线段垂直平分线上的点到线段两端的距离相等”的逆命题,并证明这个逆命题是真命题.解:这个定理的逆命题是: 到线段两端点距离相等的点在线段的垂直平分线上.已知:如图,AB是一条线段,P是一点,且PA=PB求证:点P在线段AB的垂直平分线上作PC⊥AB于点O OC证明:∵PA=PB,PO⊥AB∴OA=OB(等腰三角形三线合一性质)∴PC是AB的垂直平分线∴点P在线段AB的垂直平分线上(1)当点P在线段AB上,结论显然成立;(2)当点P不在线段AB上时线段垂直平分线性质定理: 到线段两端距离相等的点在线段的垂直平分线上.几何语言: ∵PA=PB∴点P在AB的垂直平分线上 线段垂直平分线上的点到线段两端的距离相等.线段垂直平分线性质定理的逆定理: 例2 说出命题“两个全等三角形的面积相等”的逆命题,判断这个命题的真假,并说明理由.解:逆命题是 “ 如果两个三角形的面积相等,那么这两个三角形全等.”DF分析:说明一个命题是真命题需经证明,而说明一个命题是假命题只需举一个反例.1.写出下列各命题的逆命题,并判断原命题和逆命题的真假:(1)同位角相等; (2)如果|a|=|b|,那么a=b; (3)等边三角形的三个角都是60°逆命题:相等的角是同位角 逆命题:如果a=b,那么|a|=|b| 逆命题:三个角都是60°的三角形是等边三角形 真命题假命题真命题真命题真命题真命题2.下列定理中,哪些有逆定理?如果有逆定理,请说出逆定理.(1)平行四边形的两组对边分别平行; (2)对角线互相平分的四边形是平行四边形; (3)三角形的中位线平行于第三边.两组对边分别平行的四边形是平行四边形 平行四边形的对角线互相平分 没有逆定理 有逆定理有逆定理3. 已知命题:“P是等边三角形ABC内一点.若点P到三边的距离相等,则PA=PB=PC.”证明这个命题,并写出它的逆命题,判断其逆命题成立吗?4.已知,如图ABC中,边AB与BC的中垂线交于点P,求证:P点也在AC的中垂线上.5.说出命题“如果一个四边形是平行四边形,那么它的一条对角线把它分为两个全等三角形”的逆命题,判断这个命题的真假,并给出证明.1. 逆命题、逆定理的概念: 在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.我们把其中的一个叫做原命题,另一个叫做它的逆命题. 如果一个定理的逆命题能被证明是真命题,那么它是原定理的逆定理,这两个定理叫做互逆定理.2. 线段垂直平分线的定理和逆定理线段垂直平分线性质定理: 到线段两端距离相等的点在线段的垂直平分线上.线段垂直平分线上的点到线段两端的距离相等.线段垂直平分线性质定理的逆定理:
2.5 逆命题和逆定理浙教版《数学》八年级上册教学目标1.经历逆命题概念的发生过程,了解一个命题都是由条件与结论两部分构成,每个命题都有它的逆命题,命题由真假之分;2.了解逆命题、逆定理的概念.探索线段垂直平分线性质定理的逆定理,培养学生敢于面多挑战和勇于克服困难的意志.通过认识两个命题是不是逆命题,在简单情况下写出一个命题的逆命题,提高学生的表达能力和说理的条理性.1. 下列句子是命题的是 ( ) A.画∠AOB=45° B. 小于直角的角是锐角吗? C.连结CD D. 飞机是会飞的交通工具对某件事作出正确或不正确判断的句子叫做命题D命题由条件、结论组成正确的命题是真命题,错误的命题是假命题命题的定义:命题的结构:命题有真有假: 观察表中的命题,命题⑴与命题⑵,命题⑶与命题⑷的条件和结论有什么关系?a=ba2=b2a2=b2a=b两直线平行同位角相等同位角相等两直线平行填表 在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.我们把其中的一个叫做原命题,另一个叫做它的逆命题.说出下列命题的逆命题,并判定原命题和逆命题的真假:圆既是中心对称,又是轴对称的图形.平行四边形有一组对边平行且相等.高速行驶时不接触地面的交通工具是磁悬浮列车.(1)既是中心对称,又是轴对称的图形是圆.(2)有一组对边平行且相等的四边形是平行四边形.(3)磁悬浮列车是一种高速行驶时不接触地面的交通 工具.真命题假命题假命题真命题真命题真命题 如果一个定理的逆命题能被证明是真命题,那么就叫它是原定理的逆定理,这两个定理叫互逆定理.注:逆定理、互逆定理一定都是真命题.下列定理中,哪些有逆定理?如果有逆定理,请说出逆定理.(1)同旁内角互补,两直线平行;(2)对顶角相等;(3)三角形的两边之和大于第三边.没有逆定理两直线平行,同旁内角互补.没有逆定理有逆定理判断下列说法是否正确?请说明理由(1)假命题没有逆命题; (2)真命题没有逆命题; (3)每个命题都有逆命题; (4)真命题的逆命题是真命题; √×××(5)每个定理都有逆定理;×(6)逆定理有真有假.×例1 说出定理“线段垂直平分线上的点到线段两端的距离相等”的逆命题,并证明这个逆命题是真命题.解:这个定理的逆命题是: 到线段两端点距离相等的点在线段的垂直平分线上.已知:如图,AB是一条线段,P是一点,且PA=PB求证:点P在线段AB的垂直平分线上作PC⊥AB于点O OC证明:∵PA=PB,PO⊥AB∴OA=OB(等腰三角形三线合一性质)∴PC是AB的垂直平分线∴点P在线段AB的垂直平分线上(1)当点P在线段AB上,结论显然成立;(2)当点P不在线段AB上时线段垂直平分线性质定理: 到线段两端距离相等的点在线段的垂直平分线上.几何语言: ∵PA=PB∴点P在AB的垂直平分线上 线段垂直平分线上的点到线段两端的距离相等.线段垂直平分线性质定理的逆定理: 例2 说出命题“两个全等三角形的面积相等”的逆命题,判断这个命题的真假,并说明理由.解:逆命题是 “ 如果两个三角形的面积相等,那么这两个三角形全等.”DF分析:说明一个命题是真命题需经证明,而说明一个命题是假命题只需举一个反例.1.写出下列各命题的逆命题,并判断原命题和逆命题的真假:(1)同位角相等; (2)如果|a|=|b|,那么a=b; (3)等边三角形的三个角都是60°逆命题:相等的角是同位角 逆命题:如果a=b,那么|a|=|b| 逆命题:三个角都是60°的三角形是等边三角形 真命题假命题真命题真命题真命题真命题2.下列定理中,哪些有逆定理?如果有逆定理,请说出逆定理.(1)平行四边形的两组对边分别平行; (2)对角线互相平分的四边形是平行四边形; (3)三角形的中位线平行于第三边.两组对边分别平行的四边形是平行四边形 平行四边形的对角线互相平分 没有逆定理 有逆定理有逆定理3. 已知命题:“P是等边三角形ABC内一点.若点P到三边的距离相等,则PA=PB=PC.”证明这个命题,并写出它的逆命题,判断其逆命题成立吗?4.已知,如图ABC中,边AB与BC的中垂线交于点P,求证:P点也在AC的中垂线上.5.说出命题“如果一个四边形是平行四边形,那么它的一条对角线把它分为两个全等三角形”的逆命题,判断这个命题的真假,并给出证明.1. 逆命题、逆定理的概念: 在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.我们把其中的一个叫做原命题,另一个叫做它的逆命题. 如果一个定理的逆命题能被证明是真命题,那么它是原定理的逆定理,这两个定理叫做互逆定理.2. 线段垂直平分线的定理和逆定理线段垂直平分线性质定理: 到线段两端距离相等的点在线段的垂直平分线上.线段垂直平分线上的点到线段两端的距离相等.线段垂直平分线性质定理的逆定理:
相关资料
更多









