浙教版（2024）八年级上册第2章 特殊三角形2.5 逆命题和逆定理教课ppt课件

这是一份浙教版（2024）八年级上册第2章 特殊三角形2.5 逆命题和逆定理教课ppt课件，共21页。PPT课件主要包含了学习目标，命题的概念，命题的结构，它的对角线互相平分，回顾旧知，a＝b，a2＝b2，两直线平行，同位角相等，不一定等内容，欢迎下载使用。

1.了解逆命题、逆定理的概念.2.经历逆命题的概念的发生过程，了解一个命题都是由条件与结论两部分构成，每个命题都有它的逆命题，命题有真假之分.
对某一件事情作出正确或不正确的判断的句子叫做命题.
命题：“平行四边形的对角线互相平分”条件是_____________________________，结论是__________________________ .
命题：“对角线互相平分的四边形是平行四边形” 条件是__________________________________，结论是__________________________         
条件和结论，它的一般形式是“如果……，那么……”
有一个四边形是平行四边形
有一个四边形的对角线互相平分
这个四边形是平行四边形
命题有真有假.正确的命题是真命题，错误的命题是假命题.
“飞机是会飞的交通工具”“会飞的交通工具是飞机”
这两个命题有什么不同？它们都是真命题吗？
第一个命题的条件是第二个命题的结论，第二个命题的结论是第一个命题的条件
⑷如果a2＝b2，那么a＝b.
⑶如果a＝b，那么a2＝b2.
⑵同位角相等，两直线平行
⑴两直线平行，同位角相等
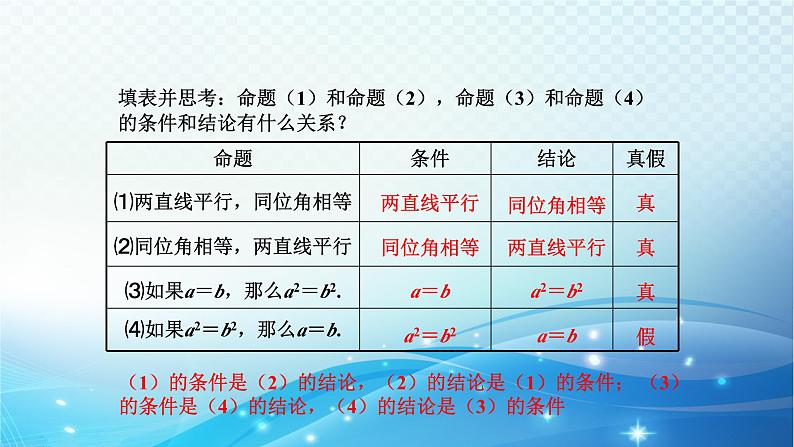
填表并思考：命题（1）和命题（2），命题（3）和命题（4）的条件和结论有什么关系？
（1）的条件是（2）的结论，（2）的结论是（1）的条件； （3）的条件是（4）的结论，（4）的结论是（3）的条件
在两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论是第二个命题的条件，那么这两个命题叫做互逆命题.
　　我们把其中的一个叫做原命题，另一个叫做它的逆命题.
上表中，命题（1）与命题（2），命题（3）与命题（4）都是互逆命题
每个命题都有它的逆命题，但每个真命题的逆命题是否一定为真命题？
如果一个定理的逆命题能被证明是真命题，那么就叫它是原定理的逆定理，这两个定理叫互逆定理.
1.说出下列命题的逆命题，并判定逆命题的真假：（1）有一组对边平行且相等的四边形是平行四边形.（2）磁悬浮列车是一种调整行驶时不接触地面的交通工具.
逆命题：平行四边形有一组对边平行且相等.
高速行驶时不接触地面的交通工具是磁悬浮列车.
2.说出两对互逆的定理
（2）同旁内角互补,两直线平行.
例1 说出定理“线段垂直平分线上的点到这条线段两个端点的距离相等”的逆命题，并证明这个逆命题是真命题.
解:　这个定理的逆命题是: 到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．
已知：AB是一条线段，Ｐ是一点，且PA＝PB
求证：点Ｐ在线段AB的垂直平分线上
（2）当点P不在 线段AB上时，作PC⊥AB于点O.
证明（1）当点P在线段ＡＢ上，结论显然成立；
∵PA=PB，PO⊥AB，
∴OA=OB（等腰三角形三线合一）
∴PC是AB的垂直平分线.
∴点P在线段AB的垂直平行线上
可见，线段垂直平分线性质定理的逆定理是真命题.
到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．
线段垂直平分线性质定理的逆定理：
例2　写出命题“两个全等三角形的面积相等”的逆命题，判断这个命题的真假，并给出证明.
解　逆命题是 “ 如果两个三角形的面积相等，那么这两个三角形全等”
这个逆命题是假命题.举反例如下：
如图，在△ABC和△ABE中，CD，EF分别是△ABC和△ABE的AB边上的高线，且CD=EF，则△ABC和△ABE的面积相等，但显然它们不全等.所以这个逆命题是假命题.
定理“直角三角形斜边上的中线等于斜边的一半”的逆命题是______，这个命题正确吗？若正确，请你证明这个命题，若不正确请说明理由．
逆命题是“三角形一边上的中线是这边的一半的话，那么这个三角形是直角三角形” 这个命题是正确的． 已知：△ABC中，D是AC的中点，BD=AD，BD=DC． 求证：△ABC是直角三角形．
证明：∵BD=AD， ∴∠A=∠ABD， ∵BD=DC， ∴∠C=∠DBC， ∵∠A+∠C+∠ABD+∠DBC=180°， ∴2（∠A+∠C）=180°， 解得∠A+∠C=90°， ∴∠ABC=90°． 即△ABC是直角三角形．
1.下列命题的逆命题是真命题的有（　　） （1）四边形是多边形；（2）两直线平行，同旁内角互补； （3）若ab=0，则a=0或b=0；（4）三角形中等角对等边． A．1个 B．2个 C．3个 D．4个
（1）其逆命题是：多边形是四边形，错误； （2）其逆命题是：如果同旁内角互补，则两直线平行，正确； （3）其逆命题是：若a=0或b=0，则ab=0，正确； （4）其逆命题是：三角形中等边对等角，正确． 所以真命题的有三个． 故选C．
A.任何命题都有逆命题，正确，故本选项错误； B.任何定理不一定都有逆定理，故本选项正确； C.真命题的逆命题不一定为真，正确，故本选项错误； D.任何命题都是由条件和结论构成的，正确，故本选项错误． 故选B．
2.下列说法错误的是（　　）
3.写出下列命题的逆命题，并判断这些命题的真假. （1）如果∠α与∠β是邻补角，那么∠α+∠β=180°； （2）如果一个三角形的两个内角相等，那么这两个内角所对的边相等.
解：（1）逆命题：如果∠α+∠β=180°，那么∠α与∠β是邻补角.这是假命题. （2）逆命题：如果一个三角形的两条边相等，那么这两条边所对的内角相等.这是真命题.
4.说出命题“等腰三角形两腰上的高相等”的逆命题，并判断逆命题的真假．若逆命题是真命题，请加以证明；若逆命题是假命题，请举出反例．
5.写出符合下列条件的一个原命题 （1）原命题和逆命题都是真命题； （2）原命题是假命题,但逆命题是真命题； （3）原命题是真命题,但逆命题是假命题； （4）原命题和逆命题都是假命题；
答案不唯一（1）若x=0或x=1,则x（x-1）=0 （2）若x（x-1）=0,则x=0 （3）若x=0,则x（x-1）=0 （4）若x=0,则x-1=0
（1）“对顶角相等”这个命题正确，但它的逆命题“相等的角是对顶角”却是错的．故错误． （2）“对顶角相等”这个定理没逆定理．故正确． （3）如a²＞b²，则a＞b”的逆命题是：如a＞b，则a² ＞ b² ，假设a=1，b=-2，此时a＞b，但a² ＜ b² ，即此命题为假命题．
写出命题“如果一个三角形是直角三角形，那么它的两个锐角的角平分线所夹的锐角是45°”的逆命题，并证明这个命题是真命题．
逆命题是：如果一个三角形的两个角的角平分线所夹的锐角是45°，那么这个三角是直角三角形．
已知：如图，△ABC中，BE是∠ABC的角平分线，交AC于E，AD是∠CAB的角平分线，交BC于D，BE和AD相交于O点，且∠EOA=45°． 求证：△ABC是直角三角形