21.2.3 二次函数y＝a(x＋h)2的图象和性质 沪科版九年级数学上册课件

这是一份21.2.3 二次函数y＝a(x＋h)2的图象和性质 沪科版九年级数学上册课件，共17页。

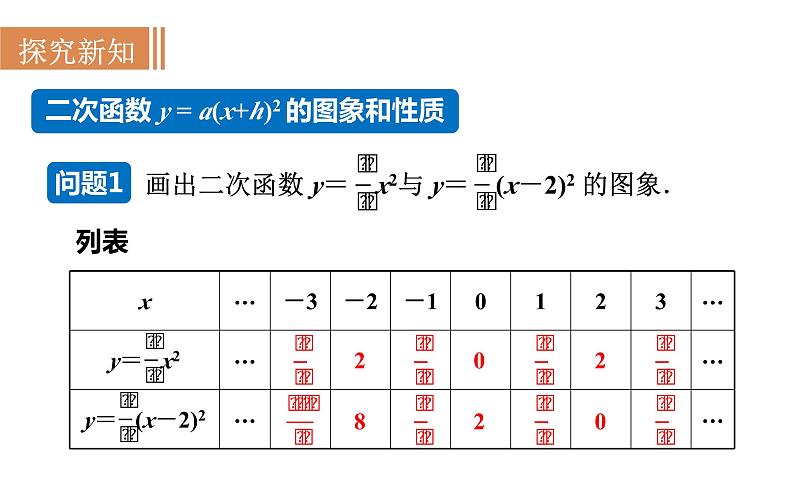
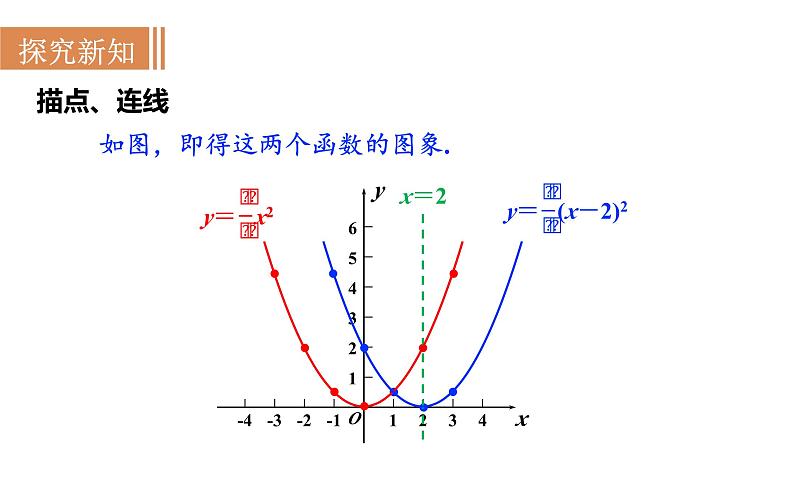
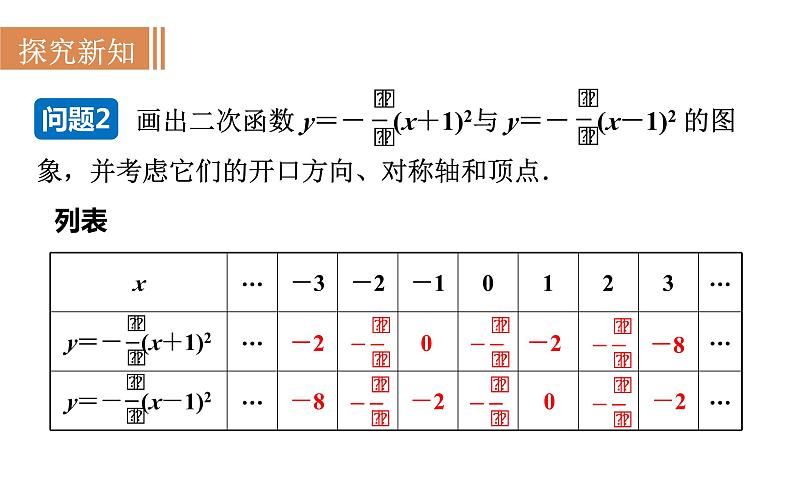
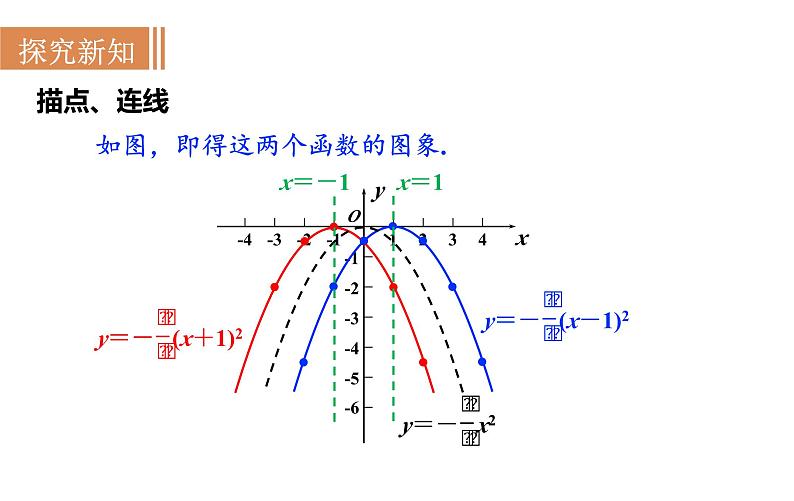
第二十一章 二次函数与反比例函数21.2 二次函数的图象和性质第3课时 二次函数y＝a(x＋h)2的图象和性质旧知回顾1．y＝ax2＋k 是由 y＝ax2 平移______个单位得到．2．二次函数 y＝x2＋5 的图象是一条________，它的开口向_____，对称轴是_____轴，顶点坐标是________；在对称轴的左侧，y 随 x 的增大而_______，在对称轴的右侧，y 随 x 的增大而_______；当 x＝____时，y 取最_____值．| k |抛物线上y(0，5)减小增大0小二次函数 y = a(x+h)2 的图象和性质问题1列表202820描点、连线如图，即得这两个函数的图象.x＝2观察图象，填写下表：向上向上y轴直线 x＝2(0，0)(2，0)问题2列表－20－2－8－8－20－2描点、连线如图，即得这两个函数的图象.x＝－1x＝1观察图象，填写下表：向下直线 x＝－1(－1，0)直线 x＝0直线 x＝1向下向下(0，0)(1，0)向上向下直线 x＝h直线 x＝h(h，0)(h，0)当x=h时，y最小值=0当x=h时，y最大值=0当x＜h时，y随x的增大而减小；x＞h时，y随x的增大而增大.当x＞h时，y随x的增大而减小；x＜h时，y随x的增大而增大.练一练：若抛物线 y＝3(x＋ )2的图象上的三个点，A(－3 ，y1)，B(－1，y2)，C(0，y3)，则y1，y2，y3的大小关系为_______________．解析：∵抛物线y＝3(x＋ )2的对称轴为x＝－ ，a＝3＞0， ∴x＜－ 时，y随x的增大而减小； x＞－ 时，y随x的增大而增大． ∵点A的坐标为(－3 ，y1)， ∴点A在抛物线上的对称点A′的坐标为( ，y1)． ∵－1＜0＜ ， ∴y2＜y3＜y1.y2＜y3＜y1二次函数 y=ax2 与 y=a(x+h)2 的关系向右平移1个单位向左平移1个单位??左右平移规律： 括号内左加右减；括号外不变. 将二次函数 y＝－2x2 的图象平移后，可得到二次函数 y＝－2(x＋1)2 的图象，平移的方法是 (　　)A．向上平移1个单位　 　B．向下平移1个单位 C．向左平移1个单位　 　D．向右平移1个单位例1解析：抛物线 y＝－2x2的顶点坐标是(0，0)，抛物线 y＝－2(x＋1)2的顶点坐标是(－1，0)．则由二次函数 y＝－2x2的图象向左平移1个单位即可得到二次函数 y＝－2(x＋1)2的图象．故选C.C 抛物线 y＝ax2 向右平移3个单位后经过点(－1，4)，求a的值和平移后的函数关系式．例2解：二次函数 y＝ax2 的图象向右平移3个单位后的二次函数关系式可表示为y＝a(x－3)2，把 x＝－1，y＝4代入，得4＝a(－1－3)2，a＝ ，∴平移后二次函数关系式为y＝ (x－3)2.提示：根据抛物线左右平移的规律，向右平移3个单位后，a不变，括号内应“减去3”；若向左平移3个单位，括号内应“加上3”，即“左加右减”．．1．把抛物线 y＝－x2 沿着 x 轴方向平移3个单位长度，平移后抛物线的解析式是____________________________.2．二次函数 y＝2(x－ )2 图象的对称轴是直线_______，顶点是_________.3．若(－ ，y1)，(－ ，y2)，( ，y3)为二次函数 y＝(x－2)2 图象上的三点，则 y1，y2 ，y3 的大小关系为_______________. y＝－(x＋3)2 或 y＝－(x－3)2 y1 ＞y2 ＞ y34．抛物线 y＝－3(x＋3)2，当 x________时，y 随 x 的增大而增大；当 x________时，y 随 x 的增大而减小．5．抛物线 y＝a(x＋h)2 的顶点为(－2，0)，它的形状与 y＝3x2 相同，但开口方向与之相反．(1)求抛物线解析式；(2)求抛物线与 y 轴交点坐标．解：(1)由题意得 y＝－3(x＋2)2； (2)当x＝0时，y＝－12，与y轴交点(0，－12)．＜－3＞－3