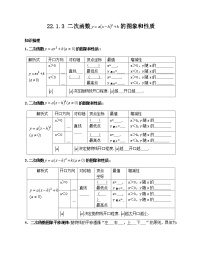
人教版九年级上册22.1.3 二次函数y＝a（x－h）2＋k的图象和性质第一课时导学案

这是一份人教版九年级上册22.1.3 二次函数y＝a（x－h）2＋k的图象和性质第一课时导学案，共4页。学案主要包含了学习任务一，学习任务二，学习任务三等内容，欢迎下载使用。
学习任务单课程基本信息学科数学年级九年级学期春季课题22.1.3 二次函数y =a(x-h)2 + k 的图象和性质（第一课时）教科书书  名：义务教育教科书 数学 九年级 上册 教材出版社：人民教育出版社            出版日期：2014年3月学生信息姓名学校班级学号    学习目标1.能用描点法画出二次函数y = ax2＋k的图象，了解图象特征和性质，体会数形结合的思想.2.了解二次函数y = ax2＋k的图象与y = ax2图象的关系，体会转化思想.3.类比二次函数y = ax2的研究过程，探究二次函数y = ax2＋k的图象和性质，体会研究二次函数图象和性质的一般方法．课前学习任务回顾二次函数y = ax2的图象特征和性质以及研究的过程.课上学习任务【学习任务一】
在同一直角坐标系中，画出二次函数，的图象． 1.列表
2.描点、连线思考：抛物线，的开口方向、对称轴和顶点各是什么？【学习任务二】
思考：（1）k的取值对图象的位置有何影响？（2）抛物线y = ax2＋k 与抛物线y = ax2有什么关系？归纳：随着k的变化，二次函数y = ax2＋k的图象在          或          平移.当k >0时，把抛物线y = ax2        平移       个单位长度，就得到抛物线y = ax2＋k ；当k <0时，把抛物线y = ax2        平移        个单位长度，就得到抛物线y = ax2＋k.  二次函数y＝ax2＋k的图象和性质【学习任务三】练习1. 在同一直角坐标系中，画出下列二次函数的图象：y = 2x2， y = 2x2＋1，y = 2x2－1．（1）观察三条抛物线的位置关系，并分别指出它们的开口方向、对称轴和顶点. （2）你能说出抛物线y = 2x2＋k的开口方向、对称轴和顶点吗？它与抛物线y = 2x2有什么关系？（1）答：列表：描点、连线：           小结：图象的位置关系：把抛物线y = 2x2                    ，就得到抛物线y = 2x2＋1 ；把抛物线y = 2x2                    ，就得到抛物线y = 2x2－1. （2）答：抛物线y =2x2＋k的开口       ，对称轴为        ，顶点为          . 当k >0时，把抛物线y = 2x2       平移       单位长度，就得到抛物线y = 2x2＋k ；当k <0时，把抛物线y = 2x2       平移       单位长度，就得到抛物线y = 2x2＋k. 2.（1）抛物线y = −2x2＋3的开口向            ，对称轴为            ，顶点为          .当x <          时，y随x的增大而增大 ；当x >          时，y随x的增大而减小；当x=           时，y取最       值，为       .  （2）抛物线y= −2x2 －2可由抛物线y= −2x2向           平移            单位长度得到. 推荐的学习资源