【同步讲义】（苏教版2019）高中数学必修二：第26讲 互斥事件和独立事件 讲义

第26讲  互斥事件和独立事件

知识点01  互斥事件和对立事件

1.互斥事件的定义

对于事件A和事件B，若AB=Ø，即事件A与B不可能          发生。这时，我们称A，B为          。

2.对立事件的定义

对于事件A和事件C，若AC=Ø，并且A+C=Ω，即互斥事件A，C中必有          发生。这时，我们称A，C为          ，记作或。

【微点拨】若两个事件对立，则这两个事件是互斥事件；反之，若两个事件是互斥事件，则这两个事件未必是对立事件。对立事件是特殊的互斥事件，若事件A，B是对立事件，则事件A与事件B互斥，而且A∪B是必然事件。

3.概率的加法公式

(1)如果事件A，B互斥，那么事件A+B发生的概率，等于事件A，B分别发生的概率的          ，即P(A+B)=          。

(2)互斥事件可以推广到n个事件的情形(n∈N，n>2)：如果事件 中任何两个事件都是互斥事件，那么称事件 两两互斥。如果事件，两两互斥，那么

。

4.随机事件的概率的其他常用性质

（1）         

（2）当A⊆B时，          ；

（3）当A，B不互斥时，          。

【微点拨】(1)概率的加法公式的应用前提是“事件A与事件B互斥”，否则不可用.对立事件的概率公式使用的前提必须是对立事件，否则不能使用。

(2)当一个事件的概率不易直接求出，但其对立事件的概率易求时，可运用对立事件的概率公式，即可使用间接法求概率。

【即学即练1】如图，随机事件A，B互斥，记分别为事件A，B的对立事件，那么（　　）

A．A∪B是必然事件  B．∪是必然事件

C．与一定互斥  D．与一定不互斥

知识点02  相互独立事件

1.相互独立事件的定义

一般地，如果事件A是否发生不影响事件B发生的概率，那么称A，B为          事件。

事件A，B相互独立          。

2.性质：如果事件A与事件B相互独立，那么A与B，A与B， 与也相互          。

3.独立事件可以推广到n个事件的情形(n∈N，n>2)。一般地，如果事件相互独立，那么

4.相互独立事件与互斥事件的概率计算

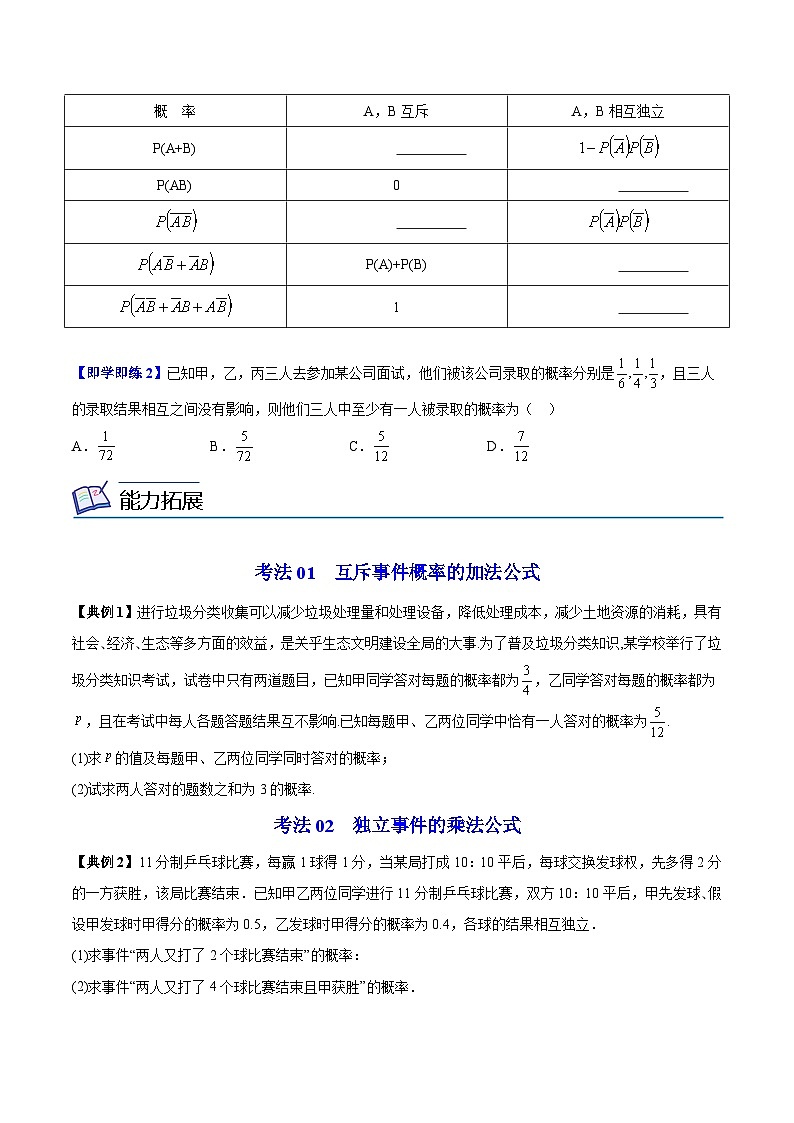
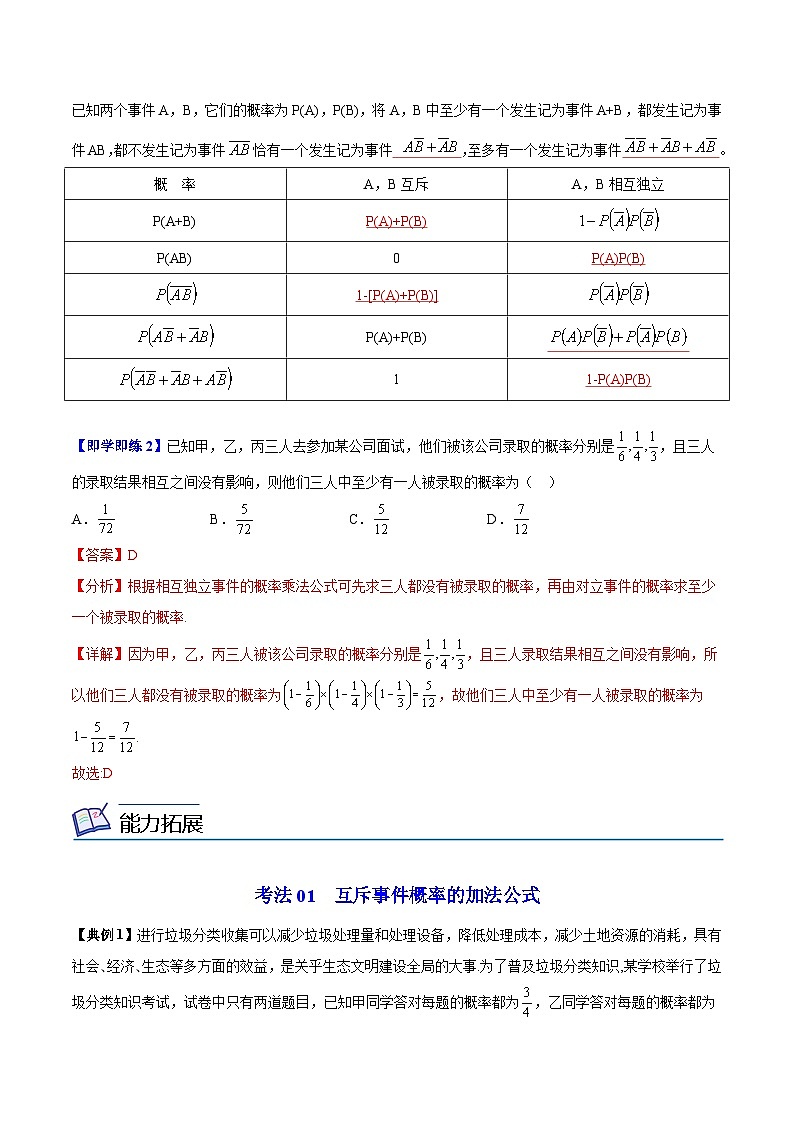
已知两个事件A，B，它们的概率为P(A)，P(B)，将A，B中至少有一个发生记为事件A+B，都发生记为事件AB，都不发生记为事件恰有一个发生记为事件          ，至多有一个发生记为事件          。

【即学即练2】已知甲，乙，丙三人去参加某公司面试，他们被该公司录取的概率分别是，且三人的录取结果相互之间没有影响，则他们三人中至少有一人被录取的概率为（    ）

A． B． C． D．

考法01  互斥事件概率的加法公式

【典例1】进行垃圾分类收集可以减少垃圾处理量和处理设备，降低处理成本，减少土地资源的消耗，具有社会､经济､生态等多方面的效益，是关乎生态文明建设全局的大事.为了普及垃圾分类知识,某学校举行了垃圾分类知识考试，试卷中只有两道题目，已知甲同学答对每题的概率都为，乙同学答对每题的概率都为，且在考试中每人各题答题结果互不影响.已知每题甲、乙两位同学中恰有一人答对的概率为.

(1)求的值及每题甲、乙两位同学同时答对的概率；

(2)试求两人答对的题数之和为3的概率.

考法02  独立事件的乘法公式

【典例2】11分制乒乓球比赛，每赢1球得1分，当某局打成10：10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束．已知甲乙两位同学进行11分制乒乓球比赛，双方10：10平后，甲先发球､假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立．

(1)求事件“两人又打了2个球比赛结束”的概率：

(2)求事件“两人又打了4个球比赛结束且甲获胜”的概率．

题组A  基础过关练

1．下列说法正确的是（　　）

A．互斥事件与对立事件含义相同

B．互斥事件一定是对立事件

C．对立事件一定是互斥事件

D．对立事件可以是互斥事件，也可以不是互斥事件

2．下列各组事件中，是对立事件的是（    ）

A．一名射手在一次射击中，命中环数大于6与命中环数小于8

B．统计一个班的数学成绩，平均分不低于90分与平均分不高于90分

C．掷一枚骰子，向上点数为奇数与向上点数为偶数

D．某人连续投篮三次，恰有两次命中与至多命中一次

3．采用随机模拟的方法估计某运动员射击4次，至少击中3次的概率.先由计算机给出0到9之间取整数值的随机数，指定0，1表示没有击中目标，2，3，4，5，6，7，8，9表示击中目标，以4个随机数为一组，代表射击4次的结果，经随机模拟产生了20组随机数:

根据以上数据估计该射击运动员射击4次至少击中3次的概率为（    ）

A．0.852 B．0.8192 C．0.8 D．0.75

4．已知事件A，B，C两两互斥，若，，，则（    ）．

A． B． C． D．

5．某单位入职面试中有三道题目，有三次答题机会，一旦某次答对抽到的题目，则面试通过，否则就一直抽题到第3次为止.若求职者小王答对每道题目的概率都是，则他最终通过面试的概率为（    ）

A． B． C． D．

6．从m名男生和n名女生中任选3人去参加演讲比赛，所选3人中至少有1名女生的概率为，那么所选3人都是男生的概率为______.

7．若，为互斥事件，，，则______.

8．若事件A、B是对立事件，则______.

9．盒子中有散落的黑白棋子若干粒，已知从中取出粒都是黑子的概率是，从中取出粒都是白子的概率是，则从中任意取出粒恰好是一粒黑子一粒白子的概率是______.

10．某商场有奖销售中，购满100元商品得1张奖券，多购多得．1000张奖券为一个开奖单位，设特等奖1个，一等奖10个，二等奖50个，其余均为不中奖．设1张奖券中特等奖、一等奖、二等奖的事件分别为，，，求：

(1)事件，，的概率；

(2)1张奖券的中奖概率；

(3)1张奖券不中特等奖且不中一等奖的概率．

题组B  能力提升练

1．若甲､乙､丙在10分钟之内独立复原魔方的概率分别为，则甲､乙､丙至多有一人在10分钟之内独立复原魔方的概率为（    ）

A．0.26 B．0.29 C．0.32 D．0.35

2．袋内分别有红､白､黑球个，从中任取2个，则互斥而不对立的两个事件是（    ）

A．至少有一个白球；都是白球 B．至少有一个白球；至少有一个红球

C．恰有一个白球；一个白球一个黑球 D．至少有一个白球；红､黑球各一个

3．已知事件A与事件B是互斥事件，则（    ）

A． B．

C． D．

4．从装有2个红球和2个黑球的口袋中任取2个球，那么互斥而不对立的两个事件是（    ）

A．至少有1个黑球与都是黑球 B．至少有1个黑球与至少有1个红球

C．至少有1个黑球与都是红球 D．恰有1个黑球与恰有2个黑球

5．现有7名世界杯志愿者，其中，，通晓日语，，通晓韩语，，通晓葡萄牙语，从中选出通晓日语、韩语、葡萄牙语志愿者各一名组成一个小组，则，不全被选中的概率为______．

6．甲、乙、丙三名同学将参加2023年高考，根据高三年级半年来的各次测试数据显示，甲、乙、丙三人数学能考135分以上的概率分别为，和.设三人是否考135分以上相互独立，则这三人在2023年高考中至少有两人数学考135分以上的概率为_____________.

7．某小组有3名男生和2名女生，从中任选出2名同学去参加演讲比赛，有下列4对事件：

①至少有1名男生和至少有1名女生，②恰有1名男生和恰有2名男生，

③至少有1名男生和全是男生，④至少有1名男生和全是女生，

其中为互斥事件的序号是__．

8．袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率是，黑球或黄球的概率是，绿球或黄球的概率也是.求从中任取一球，得到黑球、黄球和绿球的概率分别是多少？

9．在一个不透明的盒子里装有大小、质地完全相同的球12个，其中5红、4黑、2白、1绿，从中任取1个球.记事件A为“取出的球为红球”，事件B为“取出的球为黑球”，事件C为“取出的球为白球”，事件D为“取出的球为绿球”.求:

(1)“取出的球为红球或黑球”的概率;

(2)“取出的球为红球或黑球或白球”的概率.

10．某校团委举办“喜迎二十大，奋进新征程”知识竞赛.比赛共分为两轮，每位参赛选手均须参加两轮比赛，若其在两轮比赛中均胜出，则视为赢得比赛.已知在第一轮比赛中，选手甲、乙胜出的概率分别为，，在第二轮比赛中，甲、乙胜出的概率分别为，.甲、乙两人在每轮比赛中是否胜出互不影响.

(1)从甲、乙两人中选取1人参加比赛，派谁参赛赢得比赛的概率更大？

(2)若甲、乙两人均参加比赛，求两人中至少有一人赢得比赛的概率.

题组C  培优拔尖练

1．从一批产品（既有正品也有次品）中随机抽取三件产品，设事件A=“三件产品全不是次品”，事件B=“三件产品全是次品”，事件C=“三件产品有次品，但不全是次品”，则下列结论中不正确的是（    ）

A．A与C互斥 B．B与C互斥

C．A、B、C两两互斥 D．A与B对立

2．已知，，，则事件与的关系是（    ）

A．与互斥不对立 B．与对立

C．与相互独立 D．与既互斥又独立

3．（多选题）下列对各事件发生的概率判断正确的是（    ）

A．某学生在上学的路上要经过个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是，那么该生在上学路上到第个路口首次遇到红灯的概率为

B．已知集合，，集合中任取一个元素，则该元素是集合中的元素的概率为

C．甲袋中有个白球，个红球，乙袋中有个白球，个红球，从每个袋子中各任取一个球，则取到同色球的概率为

D．设两个独立事件和都不发生的概率为，发生不发生的概率与发生不发生的概率相同，则事件发生的概率是

4．（多选题）设为两个互斥的事件，且，则下列各式正确的是（    ）

A． B．

C． D．

5．2022北京冬奥会期间，吉祥物冰墩墩成为“顶流”，吸引了许多人购买，使一“墩”难求.甲､乙､丙3人为了能购买到冰墩墩，商定3人分别去不同的官方特许零售店购买，若甲､乙2人中至少有1人购买到冰墩墩的概率为，丙购买到冰墩墩的概率为，则甲，乙､丙3人中至少有1人购买到冰墩墩的概率为___________.

6．甲､乙两人组成“星队”参加猜成语活动，每轮活动由甲､乙各猜一个成语，已知甲每轮猜对的概率为，乙每轮猜对的概率为.在每轮活动中，甲和乙猜对与否互不影响，各轮结果也互不影响，则“星队”在两轮活动中猜对3个成语的概率为___________.

7．为了纪念2017年在德国波恩举行的联合国气候大会，某社区举办《“环保我参与”有奖问答比赛》活动．某场比赛中，甲、乙、丙三个家庭同时回答一道有关环保知识的问题．已知甲家庭回答正确这道题的概率是，甲、丙两个家庭都回答错误的概率是，乙、丙两个家庭都回答正确的概率是．若各家庭回答是否正确互不影响．

(1)求乙、丙两个家庭各自回答正确这道题的概率；

(2)求甲、乙、丙三个家庭中不少于2个家庭回答正确这道题的概率．

8．为普及消防安全知识，某学校组织相关知识竞赛.比赛共分为两轮，每位参赛选手均须参加两轮比赛，若其在两轮比赛中均胜出，则视为赢得比赛.已知在第一轮比赛中，选手甲、乙胜出的概率分别为，；在第二轮比赛中，甲、乙胜出的概率分别为，，甲、乙两人在每轮比赛中是否胜出互不影响.

(1)甲在比赛中恰好赢一轮的概率；

(2)从甲、乙两人中选1人参加比赛，派谁参赛赢得比赛的概率更大？

(3)若甲、乙两人均参加比赛，求两人中至少有一人赢得比赛的概率.

9．某校举行围棋比赛，甲、乙、丙三人通过初赛，进入决赛.决赛比赛规则如下：首先通过抽签的形式确定甲、乙两人进行第一局比赛，丙轮空；第一局比赛结束后，胜利者和丙进行比赛，失败者轮空，以此类推，每局比赛的胜利者跟本局比赛轮空者进行下一局比赛，直到一人累计获胜三局，则此人获得比赛胜利，比赛结束.假设每局比赛双方获胜的概率均为，且每局比赛相互独立.

(1)求比赛进行四局结束的概率；

(2)求甲获得比赛胜利的概率.

10．第56届世界乒乓球团体锦标赛于2022年在中国成都举办，国球运动又一次掀起热潮．现有甲乙两人进行乒乓球比赛，比赛采用7局4胜制，每局11分制，每赢一球得1分，选手只要得到至少11分，并且领先对方至少2分（包括2分），即赢得该局比赛．在一局比赛中，每人只发2个球就要交换发球权，如果双方比分为10：10后，每人发一个球就要交换发球权．

(1)已知在本场比赛中，前三局甲赢两局，乙赢一局，在后续比赛中，每局比赛甲获胜的概率为，乙获胜的概率为，且每局比赛的结果相互独立，求甲乙两人只需要再进行两局比赛就能结束本场比赛的概率；

(2)已知某局比赛中双方比分为8：8，且接下来两球由甲发球，若甲发球时甲得分的概率为，乙发球时乙得分的概率为，各球的结果相互独立，求该局比赛甲得11分获胜的概率．