人教版12.2 三角形全等的判定教案

12.2.4《直角三角形全等的判定》教案

一、教学目标

(一)知识与技能：1.已知斜边和直角边会作直角三角形；2.熟练掌握“斜边、直角边”，利用它判定一般三角形全等的方法判定两个直角三角形全等

(二)过程与方法：经历作图、比较、证明等探究过程，提高分析、作图、归纳、表达、逻辑推理能力.

(三)情感态度与价值观：通过探究与交流，解决一些问题，获得成功的体验，进—步激发探究的积极性.

二、教学重点、难点

重点：掌握判定两个直角三角形全等的特殊方法HL.

难点：熟练选择判定方法，判定两个直角三角形全等.

三、教学过程

回顾与思考

1.判定两个三角形全等方法____________________.

2.如图，AB⊥BE于B，DE⊥BE于E.

(1)若∠A=∠D，AB=DE. 则△ABC与△DEF______(填“全等”或“不全等”)根据______(用简写法).

(2)若∠A=∠D，BC=EF. 则△ABC与△DEF______(填“全等”或“不全等”)根据______(用简写法).

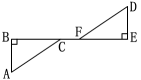(3)若AB=DE，BC=EF. 则△ABC与△DEF_______(填“全等”或“不全等”)根据______(用简写法).

若AB=DE，AC=DF，此时△ABC与△DEF还会全等吗？

探究5

1.请同学们画出以4cm、6cm为任意两边的直角三角形，并用剪刀把它剪下来与同伴进行对比观察，从中发现什么问题？

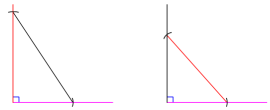
2.任意画出一个Rt△ABC，使∠C=90°，再画一个Rt△A′B′C′，使得∠C′=90°，B′C′=BC，A′B′=AB. 把画好的Rt△A′B′C′剪下，放到Rt△ABC上，它们全等吗？

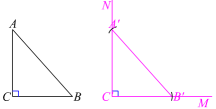
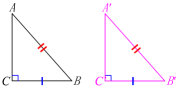
斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).

注意：
(1)“HL”定理是仅适用于Rt△的特殊方法. 因此，判定两个直角三角形全等的方法除了可以使用“SSS”、“SAS”、“ASA”、“AAS”外还可以使用“HL”.
(2)应用HL定理时，虽只有两个条件，但必须先有两个Rt△. 书写格式为：
在Rt△ABC和Rt△A′B′C′中，
∴ Rt△ABC≌Rt△A′B′C′(HL)

例5 如图，AC⊥BC，BD⊥AD，垂足分别为C，D，AC=BD.求证BC=AD.

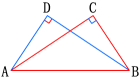证明：∵ AC⊥BC，BD⊥AD

∴ ∠C与∠D都是直角

在Rt△ABC和Rt△BAD中，

∴ Rt△ABC≌Rt△BAD (HL)
∴ BC=AD

练习

1.如图，C是路段AB的中点，两人从C同时出发，以相同的速度分别沿两条直线行走，并同时到达D、E两地. DA⊥AB，EB⊥AB. D，E与路段AB的距离相等吗？为什么？

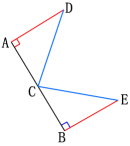解：AD=BE，理由如下：
依题意可得，AC=BC，CD=CE.

∵ DA⊥AB，EB⊥AB

∴ ∠A=∠B=90°

在Rt△ACD和Rt△BCE中，

∴ Rt△ACD≌Rt△BCE (HL)

∴ AD=BE

2.如图，AB=CD，AE⊥BC，DF⊥BC，垂足分别为E、F，CE=BF.求证AE=DF.

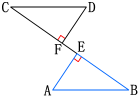证明：∵ BF=CE
∴ BF-EF=CE-EF

即 BE=CF

∵ AE⊥BC，DF⊥BC

∴ ∠AEB=∠DFC=90°

在Rt△ABE和Rt△DCF中，

∴ Rt△ABE≌Rt△DCF (HL)
∴ AE=DF

课堂小结

1.本节课你有哪些收获？2.还有没解决的问题吗？

四、教学反思

    本节课的教学主要通过分组讨论、操作探究以及合作交流等方式来进行. 在探究直角三角形全等的判定方法—“斜边、直角边”时，要让学生进行合作交流. 在寻找未知的等边或等角时，常考虑将其转移到其他三角形中，利用三角形全等来进行证明. 此外，还要注重通过适量的练习巩固所学的新知识.