


高中数学人教A版 (2019)必修 第一册3.3 幂函数一课一练
展开3.3 幂函数
一、单选题
1.若幂函数![]() 在
在![]() 上是减函数,则实数
上是减函数,则实数![]() 的值是
的值是![]()
![]()
A.![]() 或3 B.3 C.
或3 B.3 C.![]() D.0
D.0
2.设![]() ,其中a∈{-1,
,其中a∈{-1,![]() ,1,2,3},则“函数
,1,2,3},则“函数![]() 的图像经过点
的图像经过点![]() “是“函数
“是“函数![]() 在
在![]() 上单调递减”的
上单调递减”的![]()
![]()
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知![]() ,若0<a<b<1,则下列各式中正确的是 ( )
,若0<a<b<1,则下列各式中正确的是 ( )
A.f(a)<f(b)<![]() <
<![]() B.
B. ![]() <
<![]() <f(b)<f(a)
<f(b)<f(a)
C.f(a)<f(b) <![]() <
<![]() D.
D.![]() <f(a)<
<f(a)<![]() <f(b)
<f(b)
4.在同一平面直角坐标系内,函数y=xa和y=ax+![]() (a≠0)的图象可能是 ( )
(a≠0)的图象可能是 ( )
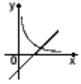
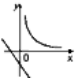
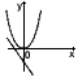
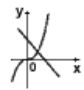
A B C D
5.幂函数![]() 的图象经过点
的图象经过点![]() ,则
,则![]()
![]()
A.是偶函数,在![]() 上单调递增
上单调递增
B.是偶函数,在![]() 上单调递减
上单调递减
C.是奇函数,在![]() 上单调递减
上单调递减
D.是非奇非偶函数,在![]() 上单调递增
上单调递增
6.下列关于幂函数![]() 的命题中正确的有
的命题中正确的有![]()
![]()
A.幂函数图象都通过点![]() ,
,![]()
B.当幂指数![]() ,3,
,3,![]() 时,幂函数
时,幂函数![]() 的图象都经过第一、三象限
的图象都经过第一、三象限
C.当幂指数![]() ,3,
,3,![]() 时,幂函数
时,幂函数![]() 是增函数
是增函数
D.若![]() ,则函数图象不通过点
,则函数图象不通过点![]() ,
,![]()
7.已知幂函数![]() 的图象经过点
的图象经过点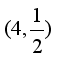 ,则
,则![]()
![]()
A.![]() B.1 C.
B.1 C.![]() D.2
D.2
8.如图所示,曲线 C1与C₂分别是函数 y=xm和y=xn在第一象限内的图象,则下列结论正确的是 ( )
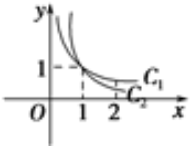
- n<m<0 B.m<n<0 C.n>m>0 D.m>n>0
二、多选题
9.下列函数中,在(-∞,-1)上是增函数的是( )
A.y=x3 B.y=-x2-4x C.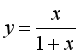 D.
D.![]()
10.若函数![]() 是幂函数,则f(x)一定( )
是幂函数,则f(x)一定( )
A.是偶函数 B.是奇函数
C.在x∈(-∞,0)上单调递减
D.在x∈(-∞,0)上单调递增
11.已知函数![]() 是幂函数,对任意
是幂函数,对任意
的值为负值,则下列结论可能成立的有( )
- a+b>0,ab<0 B.a+b<0,ab>0 C.a+b<0,ab<0 D.a+b>0,ab>0
12.已知a≠0,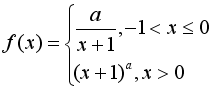 是定义在(-1,+∞)上的函数,则 ( )
是定义在(-1,+∞)上的函数,则 ( )
A.f(x)不可能为减函数 B.f(x)不可能为增函数
C.若f(x)在(0,+∞)上为增函数,则f(x)的最小值为 a
D.若f(x)在(-1,0)上为增函数,则f(x)的最大值为1
三、填空题
13.若幂函数y=(m²-2m-2)x-4m-2在(0,+∞)上单调递减,则实数m的值是 .
14.下列命题中,
①幂函数的图象不可能在第四象限;
②当![]() 时,函数
时,函数![]() 的图象是一条直线;
的图象是一条直线;
③当![]() 时,幂函数
时,幂函数![]() 是增函数;
是增函数;
④当![]() 时,幂函数
时,幂函数![]() 在第一象限内函数值随
在第一象限内函数值随![]() 值的增大而减小.
值的增大而减小.
其中正确的序号为 .
15.若![]() ,则实数m的取值范围为
,则实数m的取值范围为
16.已知幂函数![]() 的部分对应值如表:
的部分对应值如表:
| 1 |
|
| 1 |
|
则不等式![]() 的解集是 .
的解集是 .
四、解答题
17.已知幂函数![]() 的图象过点
的图象过点![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)设函数![]() 在[-1,1]是单调函数,求实数
在[-1,1]是单调函数,求实数![]() 的取值范围.
的取值范围.
18.已知幂函数y=f(x)的图象经过点 M(4,16).
(1)求f(x)的解析式.
(2)设![]()
(i)利用定义证明函数g(x)在区间[1,+∞)上单调递增;
(ii)若![]() 在[2,+∞)上恒成立,求t的取值范围
在[2,+∞)上恒成立,求t的取值范围
19.已知函数![]() 为幂函数,且为奇函数;
为幂函数,且为奇函数;
(1)求![]() 的值;
的值;
(2)求函数![]() 在
在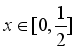 的值域.
的值域.
20.已知幂函数 ![]() (-2<m<2,且m∈Z)满足:
(-2<m<2,且m∈Z)满足:
①在区间(0,+∞)上是增函数;
②对任意的x∈R,都有f(-x)+f(x)=0.求同时满足①②的幂函数f(x)的解析式,并求当x∈[0,3]时f(x)的值域.
21.已知函数![]() 是幂函数且在
是幂函数且在![]() 上为减函数,函数
上为减函数,函数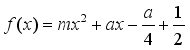 在区间[0,1]上的最大值为2,试求实数m,a的值
在区间[0,1]上的最大值为2,试求实数m,a的值
![]() 高中数学人教A版2019必修1
高中数学人教A版2019必修1
3.3 幂函数答案
一.单选题1~5 BACBD 6~8 BAA
二.多选题 9.AC 10.BD 11.BC 12.AB
三、填空题13.-1 14.①④ 15.[-1,![]() ) 16.[-4,4]
) 16.[-4,4]
四、解答题
17.【解答】解:(1)因为幂函数![]() 的图象过点
的图象过点![]() .
.
所以![]() ,解得
,解得![]() ,
,
所以函数![]() .
.
(2)![]() ,对称轴为
,对称轴为![]() ,
,
因为![]() 在[-1,1]是单调函数,所以
在[-1,1]是单调函数,所以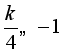 或
或![]() ,
,
解得![]() 或
或![]() ,
,
所以实k的取值范围为![]() 或
或![]() .
.
18.【解析】解:(1)设幂函数y=f(x)=xa,![]() 幂函数y=f(x) =xa的图象经过点M(4,16),∴4a=16,解得α=2,
幂函数y=f(x) =xa的图象经过点M(4,16),∴4a=16,解得α=2,
∴f(x)的解析式为f(x) =x2.
(2) 设
(i)证明:在[1,+∞)上任取1≤x1<x2,
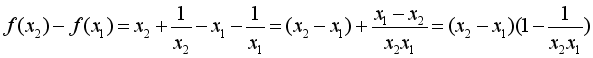
![]() 1≤x1<x2, ∴x2 -x1>0 ,
1≤x1<x2, ∴x2 -x1>0 , 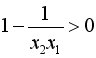
∴f(x2)-f(x1)>0,
∴函数g(x)在区间[1,+∞)上单调递增.
(ii)![]()
![]() 在[2,+∞)上恒成立,
在[2,+∞)上恒成立,
∴在[2,+∞)上,g(x)min≥![]() ,
,
由(i)得g(x)在[1,+∞)上单调递增,
∴g(x)在[2,+∞)上的最小值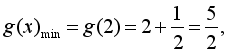
∴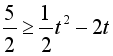 解得-1≤t≤5,∴t的取值范围是[-1,5].
解得-1≤t≤5,∴t的取值范围是[-1,5].
19.【解答】解:(1)函数![]() 为幂函数,可得
为幂函数,可得![]() ,解得
,解得![]() 或1.
或1.
当![]() 时,
时,![]() ,为奇函数.
,为奇函数.
当![]() 时,
时,![]() ,为偶函数,
,为偶函数,
![]() 为奇函数,
为奇函数,![]() .
.
综上,![]() .
.
(2)![]() 函数
函数![]() ,
, ,
,
令![]() ,可得
,可得![]() ,则
,则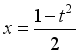 ,且
,且![]() ,
,
故当![]() 时,函数取得最小值为
时,函数取得最小值为![]() ,
,
当![]() 时,函数取得最大值为1,
时,函数取得最大值为1,
故函数的值域为[![]() ,1]
,1]
20.【解析】解:因为-2<m<2,且m∈z,所以m=-1或0或1.
因为对任意x∈R,都有f(-x)+ f(x)=0,
即f(-x)=-f(x),所以f(x)是奇函数.
当m=-1时,f(x)=x2只满足条件①而不满足条件②;
当m=1时,f(x)=x°,条件①②都不满足.
当m=0时,f(x)=x³,条件①②都满足,且在区间[0,3]上是增函数,所以当 x∈[0,3]时,函数f(x)的值域为[0,27].
21.【解答】解:因为函数![]() 是幂函数且在上为减函数,所以有
是幂函数且在上为减函数,所以有 解得
解得![]() .
.
![]()
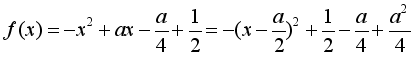 ’
’
①当![]() ,[0,1]是
,[0,1]是![]() 的单调递减区间,
的单调递减区间,
![]()
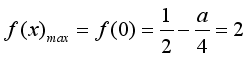
![]() ,
,![]() ’
’
②当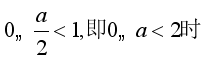 ,
,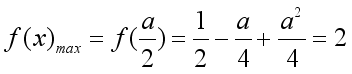 ,
,
解得![]() (舍
(舍![]() 或
或![]() (舍)
(舍)
③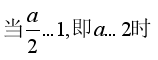 ,[0,1]为
,[0,1]为![]() 的单调递增区间,
的单调递增区间,
![]()
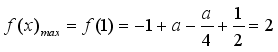 ,解得
,解得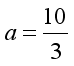 ’
’
综合①②③可知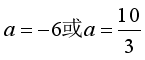
人教A版 (2019)必修 第一册3.3 幂函数练习: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4000269_t7/?tag_id=28" target="_blank">3.3 幂函数练习</a>,共8页。试卷主要包含了单选题,多选题,填空题等内容,欢迎下载使用。
人教A版 (2019)必修 第一册3.3 幂函数达标测试: 这是一份人教A版 (2019)必修 第一册3.3 幂函数达标测试,共10页。试卷主要包含了选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册3.3 幂函数课时练习: 这是一份高中数学人教A版 (2019)必修 第一册3.3 幂函数课时练习,文件包含33幂函数原卷版docx、33幂函数解析版docx等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。













