


数学必修 第二册1.1 向量精品单元测试课后练习题
展开第一章 平面向量及其应用 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共32分)
1、(4分)在菱形ABCD中,![]() ,
,![]() ,
,![]() ,P是菱形ABCD内部及边界上一点,则
,P是菱形ABCD内部及边界上一点,则![]() 的最大值是( )
的最大值是( )
A.![]() B.
B.![]() C.13 D.
C.13 D.![]()
2、(4分)已知点O为![]() 所在平面上一点,且满足
所在平面上一点,且满足![]() ,若
,若![]() 的面积与
的面积与![]() 的面积比值为
的面积比值为![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.2 D.3
C.2 D.3
3、(4分)![]() 中,
中,![]() ,则其最大内角的余弦值为( )
,则其最大内角的余弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、(4分)已知向量a,b满足![]() ,
,![]() ,
,![]() ,则a与b的夹角为( ).
,则a与b的夹角为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、(4分)已知a,b,c分别为![]() 三个内角A,B,C的对边,
三个内角A,B,C的对边,![]() ,
,![]() ,若三角形有两解,则b的可能取值是( )
,若三角形有两解,则b的可能取值是( )
A.2 B.2.3 C.3 D.4
6、(4分)若平面向量a与b的夹角为60°,![]() ,
,![]() ,则
,则![]() 等于( ).
等于( ).
A.![]() B.
B.![]() C.4 D.12
C.4 D.12
7、(4分)已知四边形ABCD的三个顶点为![]() ,
,![]() ,
,![]() ,且
,且![]() ,则顶点D的坐标为( ).
,则顶点D的坐标为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、(4分)在![]() 中,若
中,若![]() ,则
,则![]() 的形状是( ).
的形状是( ).
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不确定
二、多项选择题(共24分)
9、(6分)下列解三角形的过程中,只能有1个解的是( ).
A.![]() ,
,![]() ,
,![]() B.
B.![]() ,
,![]() ,
,![]()
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]()
10、(6分)已知![]() ,若
,若![]() 与
与![]() 互相垂直,则实数
互相垂直,则实数![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11、(6分)已知![]() 中,若
中,若![]() ,则k的取值可以是( )
,则k的取值可以是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12、(6分)在![]() 中,内角A,B,C所对的边分别为a,b,c,则下列结论正确的有( )
中,内角A,B,C所对的边分别为a,b,c,则下列结论正确的有( )
A.若![]() ,则
,则![]()
B.若![]() ,则
,则![]() 一定为等腰三角形
一定为等腰三角形
C.若![]() ,则
,则![]() 一定为直角三角形
一定为直角三角形
D.若![]() ,
,![]() ,且该三角形有两解,则边AC的范围是
,且该三角形有两解,则边AC的范围是![]()
三、填空题(共16分)
13、(4分)已知向量![]() ,且
,且![]() ,则向量
,则向量![]() 的坐标可以是_______.
的坐标可以是_______.
15、(4分)在三角形![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,则边的长为__________
,则边的长为__________
16、(4分)已知![]() 内角A,B,C的对边分别为a,b,c,那么当
内角A,B,C的对边分别为a,b,c,那么当![]() ___________时,满足条件“
___________时,满足条件“![]() ,
,![]() 的
的![]() 有两个”.(仅写出一个b的具体数值即可)
有两个”.(仅写出一个b的具体数值即可)
四、解答题(共28分)
17、(14分)已知角![]() 是
是![]() 的内角,
的内角,![]() 分别是其所对边长,向量
分别是其所对边长,向量![]() ,
,![]()
(1)求角A的大小;
(2)若![]() ,求b的长.
,求b的长.
18、(14分)三角形![]() 中,
中,![]() ,点E是边
,点E是边![]() 上的动点,当E为
上的动点,当E为![]() 中点时,
中点时,![]()
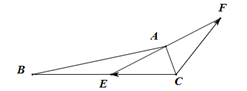
(1)求![]() 和
和![]() ;
;
(2)![]() 是
是![]() 延长线上的点,
延长线上的点,![]() ,当
,当![]() 在
在![]() 上运动时,求
上运动时,求![]() 的最大值.
的最大值.
参考答案
1、答案:B
解析:
2、答案:B
解析:
3、答案:C
解析:在![]() 中,
中,![]() ,
,
所以![]() ,
,
所以![]() 是
是![]() 的最大内角,
的最大内角,
由余弦定理知![]()
故本题正确答案为C
4、答案:C
解析:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .故选C.
.故选C.
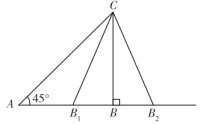
5、答案:B
解析:如图,![]() 有两解的充要条件是
有两解的充要条件是![]() ,解得
,解得![]() ,故b的取值范围是
,故b的取值范围是![]() ,结合各选项可知选B.
,结合各选项可知选B.
6、答案:B
解析:因为![]() ,所以
,所以![]() ,又因为向量a与b的夹角为60°,
,又因为向量a与b的夹角为60°,![]() ,
,
所以![]() ,所以
,所以![]() .
.
7、答案:A
解析:设顶点D的坐标为![]() ,
,
![]() ,
,![]() ,且
,且![]() ,
,
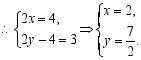 故选A.
故选A.
8、答案:A
解析:因为![]() ,
,
所以由正弦定理,可得![]() ,
,
又![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,所以
,所以![]() 为直角三角形.故选A.
为直角三角形.故选A.
9、答案:BCD
解析:根据题意,在选项A中,![]() ,因为
,因为![]() ,所以角B在
,所以角B在![]() 和
和![]() 上各有一个解,并且这两个解与角A的和都小于π,所以A不满足;在选项B中,
上各有一个解,并且这两个解与角A的和都小于π,所以A不满足;在选项B中,![]() ,
,![]() ,
,![]() ,根据余弦定理可得
,根据余弦定理可得![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() (舍去),所以只有1个解,所以B满足题意;在选项C中,条件为“边角边”,所以有唯一解,所以C满足题意;在选项D中,
(舍去),所以只有1个解,所以B满足题意;在选项C中,条件为“边角边”,所以有唯一解,所以C满足题意;在选项D中,![]() ,因为
,因为![]() ,所以角A在
,所以角A在![]() 和
和![]() 上各有一个解,当解在
上各有一个解,当解在![]() 时,角B与角A的和大于π,所以只有1个解,所以D满足题意,故选BCD.
时,角B与角A的和大于π,所以只有1个解,所以D满足题意,故选BCD.
10、答案:BD
解析:
11、答案:BD
解析:
12、答案:AC
解析:由正弦定理及大边对大角可知A正确;由![]() 可得
可得![]() 或
或![]() ,则
,则![]() 是等腰三角形或直角三角形,故B错误;由正弦定理可得
是等腰三角形或直角三角形,故B错误;由正弦定理可得![]() ,又
,又![]() ,则
,则![]() .因为
.因为![]() ,所以
,所以![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,故C正确;D结合
,故C正确;D结合![]() 及画圆弧法可知,只有
及画圆弧法可知,只有![]() 时满足条件,故D错误.故选AC.
时满足条件,故D错误.故选AC.
13、答案:![]()
解析:
14、答案:![]()
解析:
15、答案:4
解析:在![]() 中,由正弦定理:
中,由正弦定理:![]() 得:
得:![]()
又由![]() ,则
,则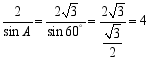 ,
,![]() ,又由
,又由![]() ,则
,则![]()
![]() ,则
,则![]() .
.![]() ,代入解得
,代入解得![]()
故本题答案为4
A
16、答案:![]()
解析:若满足条件的![]() 有两个,则
有两个,则![]() ,即
,即![]() ,所以
,所以![]() .
.
解析: (1)已知![]() ,
,
所以![]()
![]()
即![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]()
所以![]() ,所以
,所以![]()
(2)在![]() 中,
中,![]() ,
,![]()
![]()
由正弦定理知![]() ,
,
所以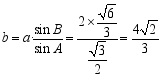 .
.
18、答案:(1)![]() (2)
(2)![]()
![]() ,解得
,解得![]()
此时![]()
由余弦定理得![]()
(2)由![]() 得
得
![]()
所以
![]()
![]()
所以,当![]() 最小即
最小即![]() 时上式最大
时上式最大
此时![]() ,所以
,所以![]() 的最大值为
的最大值为![]()
高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用练习题: 这是一份高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用练习题,共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
高中数学湘教版(2019)必修 第二册1.7 平面向量的应用举例同步训练题: 这是一份高中数学湘教版(2019)必修 第二册1.7 平面向量的应用举例同步训练题,共7页。
高中数学人教A版 (2019)必修 第二册6.1 平面向量的概念复习练习题: 这是一份高中数学人教A版 (2019)必修 第二册6.1 平面向量的概念复习练习题,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













