【单元检测】湘教版(2019)高中数学 必修第二册 第四章 立体几何初步 单元测试卷(Word版含解析)
展开第四章 立体几何初步 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共32分)
1、(4分)已知圆锥的顶点为S ,两条母线为SA,SB ,若 ![]()
![]() 的面积为
的面积为 ![]()
![]() 与圆锥的底面所成的角为
与圆锥的底面所成的角为 ![]() ,则圆锥的体积为( )
,则圆锥的体积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2、(4分)棱长都是1的三棱锥的表面积为( )
3、(4分)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5 m时,相应水面的面积为![]() ;水位为海拔157.5 m时,相应水面的面积为
;水位为海拔157.5 m时,相应水面的面积为![]() .将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5 m上升到157.5 m时,增加的水量约为
.将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5 m上升到157.5 m时,增加的水量约为![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、(4分)已知圆锥的表面积为![]() ,它的侧面展开图是一个半圆,则此圆锥的体积为( )
,它的侧面展开图是一个半圆,则此圆锥的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、(4分)如图,三棱锥![]() 的四个面都为直角三角形,
的四个面都为直角三角形,![]() 平面ABC,
平面ABC,![]() ,
,![]() ,三棱锥
,三棱锥![]() 的四个顶点都在球O的球面上,现在球O内任取一点,则该点取自三棱锥
的四个顶点都在球O的球面上,现在球O内任取一点,则该点取自三棱锥![]() 内的概率为( )
内的概率为( )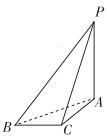
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、(4分)在轴截面顶角为直角的圆锥内,作一内接圆柱,若圆柱的表面积等于圆锥的侧面积,则圆锥的底面半径与圆柱的底面半径之比为( )
A.![]() B.2 C.
B.2 C.![]() D.4
D.4
7、(4分)已知正三棱柱的所有顶点都在球O的球面上,且该正三棱柱的底面边长为2,体积为3,则球O的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、(4分)在正方体![]() 中,过A,C,D的平面与过
中,过A,C,D的平面与过![]() 的平面的位置关系是( )
的平面的位置关系是( )
A.相交但不垂直 B.相交成60°角
C.互相垂直 D.互相平行
二、多项选择题(共24分)
9、(6分)把一张长为4宽为3的矩形白纸卷成圆柱(缝隙忽略不计),圆柱的体积是( )
10、(6分)在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,当![]() 平面EFGH时,下面结论正确的是( )
平面EFGH时,下面结论正确的是( )
A.E,F,G,H一定是各边的中点
B.G,H一定是CD,DA的中点
C.![]() ,且
,且![]()
D.四边形EFGH是平行四边形或梯形
11、(6分)已知两个完全一样的四棱锥,它们的侧棱长都等于![]() ,底面都是边长为2的正方形.下列结论成立的是( )
,底面都是边长为2的正方形.下列结论成立的是( )
A.将这两个四棱锥的底面完全重合,在得到的八面体中,有6对平行棱
B.将这两个四棱锥的底面完全重合,得到的八面体的所有顶点都在半径为![]() 的球上
的球上
C.将这两个四棱锥的一个侧面完全重合,得到的几何体共有7个面
D.将这两个四棱锥的一个侧面完全重合,这两个四棱锥的底面互相垂直
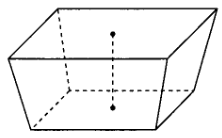
12、(6分)一棱长等于1且体积为1的长方体的顶点都在同一球的球面上,则该球的体积可能是( )
三、填空题(共16分)
13、(4分)已知正方体的外接球与内切球上各有一个动点P,Q,若线段PQ的最小值为![]() ,则正方体的棱长为_________;正方体的外接球的表面积为_______.
,则正方体的棱长为_________;正方体的外接球的表面积为_______.
14、(4分)三棱锥![]() 的顶点
的顶点![]() 均在球O的球面上,且
均在球O的球面上,且![]() ,
,![]() ,
,![]() ,则三棱锥
,则三棱锥![]() 体积的最大值为__________.
体积的最大值为__________.
15、(4分)已知圆锥的表面积等于![]() ,其侧面展开图是一个半圆,则该圆锥的体积为
,其侧面展开图是一个半圆,则该圆锥的体积为 ![]() .
.
16、(4分)三棱锥![]() 的底面是边长为3的正三角形,面PAB垂直底面ABC,且
的底面是边长为3的正三角形,面PAB垂直底面ABC,且![]() ,则三棱锥
,则三棱锥![]() 体积的最大值是_______.
体积的最大值是_______.
四、解答题(共28分)
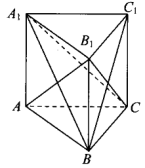
17、(14分)如图,在三棱柱![]() 中,
中,![]() ,平面
,平面![]() 平面
平面![]() .
.
证明:平面![]() 平面
平面![]() .
.
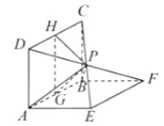
18、(14分)图1是由矩形ADEB、![]() 和菱形BFGC组成的一个平面图形,其中
和菱形BFGC组成的一个平面图形,其中![]() .将其沿AB,BC折起使得BE与BF重合,连接DG,如图2.
.将其沿AB,BC折起使得BE与BF重合,连接DG,如图2.
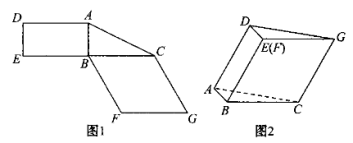
(1)证明图2中的A,C,G,D四点共面,且平面![]() 平面BCGE.
平面BCGE.
(2)求图2中的四边形ACGD的面积.
参考答案
1、答案:B
解析:
2、答案:A
解析:由题意可知三棱锥是正四面体,它的表面积就是四个三角形的面积,求出一个三角形的面积即可求解本题.
由题意可知三棱锥是正四面体,各个三角形的边长为![]() ,三棱锥的表面积就是四个全等三角形的面积,所以
,三棱锥的表面积就是四个全等三角形的面积,所以![]() ,故可知表面积为A.
,故可知表面积为A.
3、答案:C
解析:如图,由已知得该棱台的高为![]() (m),所以该棱台的体积
(m),所以该棱台的体积![]()
![]() .故选C.
.故选C.
4、答案:A
解析:设圆锥的底面半径为 ![]() ,高为
,高为 ![]() ,母线为
,母线为![]() ,
,
因为其表面积为 ![]() ,
,
所以 ![]() ,
,
即 ![]()
又因为它的侧面展开图是一个半圆,
所以 ![]() ,
,
即 ![]()
所以 ![]() ,
,
所以此圆锥的体积为![]() .
.
故选: A
5、答案:D
解析:根据题意,可以将三棱锥![]() 补全为长方体,其中长方体的底面是边长为1的正方形,高为
补全为长方体,其中长方体的底面是边长为1的正方形,高为![]() .设三棱锥
.设三棱锥![]() 外接球的半径为R,所以三棱锥
外接球的半径为R,所以三棱锥![]() 外接球的直径为长方体的体对角线,即
外接球的直径为长方体的体对角线,即![]() ,所以
,所以![]() .由于三棱锥
.由于三棱锥![]() 的体积
的体积![]() ,三棱锥
,三棱锥![]() 外接球的体积
外接球的体积![]() ,所以在球O内任取一点,该点取自三棱锥
,所以在球O内任取一点,该点取自三棱锥![]() 内的概率
内的概率 .
.
6、答案:A
解析:
7、答案:C
解析:
8、答案:C
解析:
9、答案:CD
若底面周长为![]() ,则
,则![]() ,
,![]() ,圆柱体积
,圆柱体积![]() .
.
故选:CD
10、答案:CD
解析:由![]() 平面EFGH和线面平行的性质定理,得
平面EFGH和线面平行的性质定理,得![]() ,
,![]() ,则
,则![]() ,且
,且![]() ,且
,且![]() ,所以四边形EFGH是平行四边形或梯形.故选CD.
,所以四边形EFGH是平行四边形或梯形.故选CD.
11、答案:ACD
解析:画出图形,可以得到八面体中,有6对平行棱,所以选项A正确;
如图,设AC的中点为O,计算得到![]() ,B错误;
,B错误;
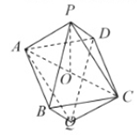
如图,分别设四棱锥![]() 的底面正方形ABCD的边AB与CD的中点为G,H,分别连接PG,PH,GH,得到的几何体共有7个面,所以选项C正确;
的底面正方形ABCD的边AB与CD的中点为G,H,分别连接PG,PH,GH,得到的几何体共有7个面,所以选项C正确;
证明平面![]() 平面ABFE,D正确.
平面ABFE,D正确.
12、答案:BCD
解析:设长方体的另外两条棱长分别为x,y,则![]() ,
,
长方体的对角线长![]() ,
,
![]() ,
,![]() ,
,![]() .
.
当且仅当![]() 时等号成立,
时等号成立,![]() ,
,
![]() .
.
结合选项可得,BCD正确,A错误.故选:BCD.
解析:
14、答案:2
解析:
15、答案:![]()
解析:![]() 则
则![]()
16、答案:![]()
解析:
17、答案:见解析.
解析:在三棱柱![]() 中,
中,
四边形![]() 为平行四边形,
为平行四边形,
因为![]() ,
,
所以四边形![]() 为菱形,
为菱形,
所以![]() ,
,
又平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
18、答案:(1)见解析.
(2)面积为4.
解析:(1)由已知得![]() ,
,
所以![]() ,故AD,CG确定一个平面,从而A,C,G,D四点共面.
,故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得![]() ,故
,故![]() 平面BCGE.
平面BCGE.
又因为![]() 平面ABC,所以平面
平面ABC,所以平面![]() 平面BCGE.
平面BCGE.
(2)取CG的中点M,连接EM,DM.
因为![]() 平面BCGE,
平面BCGE,
所以![]() 平面BCGE,故
平面BCGE,故![]() .
.
由已知,四边形BCGE是菱形且![]() 得
得![]() ,
,
故![]() 平面DEM.
平面DEM.
因此![]() .
.
在![]() 中,
中,![]() ,故
,故![]() .
.
所以四边形ACGD的面积为4.