1.4 有理数的大小比较 培优（原卷版）
展开
这是一份1.4 有理数的大小比较 培优（原卷版），共7页。
1.4有理数的大小比较培优 一、单选题1．将甲、乙、丙三个正分数化为最简分数后，其分子分别为6、15、10，其分母的最小公倍数为360．判断甲、乙、丙三数的大小关系为何？（ ）A．乙＞甲＞丙 B．乙＞丙＞甲 C．甲＞乙＞丙 D．甲＞丙＞乙2．已知a、b在数轴上对应的点如图1所示，下列结论正确的是( ) 
A．a>b B．|a|<|b| C．－a<－b D．a<－b3．把几个互不相同的数用大括号括起来，相邻两个数之间用逗号隔开，如：{1，2}，{1，4，7，…}，…，我们称之为集合，其中的每一个数称为该集合的元素，如果一个所有元素均为有理数的集合满足：当有理数x是集合的一个元素时，2018﹣x也必是这个集合的元素，这样的集合我们又称为对称集合，例如{2，2016}就是一个对称集合，若一个对称集合所有元素之和为整数M，且23117＜M＜23897，则该集合总共的元素个数是（ ）A．22 B．23 C．24 D．254．对于任意实数
，通常用
表示不超过的最大整数，如
，下列结论正确的是（ ）①
②
③
④
A．①② B．②③ C．①③ D．③④5．有下列说法：①两个有理数比较大小，绝对值大的反而小：②用一个平面去截正方体，面的形状可能是五边形；③数轴上表示两个有理数的点，较大的数表示的点离原点较远；④若a是3的相反数，则a的倒数是
；⑤一个数的绝对值等于它的相反数，这个数一定是负数．其中正确的说法有（ ）A．5个 B．4个 C．3个 D．2个6．下列说法中，正确的是（ ）A．若a≠b，则
B．若a＞|b|，则a＞bC．若|a|=|b|，则a=b D．若|a|＞|b|，则a＞b7．下列各式中，正确的是（ ）A．
B．－4＞0 C．－3＜－6 D．
8．在
，在这四个数中，绝对值最小为（ ）A．4 B．
C．
D．-5 二、填空题9．规定：[x]表示不大于x的最大整数，（x）表示不小于x的最小整数，[x）表示最接近x的整数（x≠n+0.5，n为整数），例如：[2.3]=2，（2.3）=3，[2.3）=2．当﹣1＜x＜1时，化简[x]+（x）+[x）的结果是_____．10．比较大小：①-0.3 ____ 
；②+（-5） ____ -|-17|； ③
____
．11．比较大小：﹣
__﹣
．12．比较大小：
___
.（选用＞、＜、＝号填写）13．比较大小：
______
（填“
”，“
”或“
”）．14．比较大小：(1) -(-3)_____-[+(-9)]； (2)-
____-
．15．若
，则
，
，
，
的大小关系是________．（用“”连接）16．设
，
，且
，用“” 号把，，
，
连接起来为__________．17．比较大小，用“＜”“＞”或“=”连接：-3．14_____-|-π|．三、解答题18．学习了第二章《整式的加减》，我们知道，字母可以表示数．若表示有理数，小刚认为、－、、
这四个数中，最大，－最小，你认为对吗？若不对，请举一个反例，并把这四个数从大到小排序．你能比较、－、、这四个数的大小吗？ 19．如图，数轴上有点a，b，c三点
（1）用“＜”将a，b，c连接起来．（2）b﹣a 1（填“＜”“＞”，“＝”）（3）化简|c﹣b|﹣|c﹣a+1|+|a﹣1|（4）用含a，b的式子表示下列的最小值：①|x﹣a|+|x﹣b|的最小值为 ；②|x﹣a|+|x﹣b|+|x+1|的最小值为 ；③|x﹣a|+|x﹣b|+|x﹣c|的最小值为 ． 20．若a＜0，试比较a与的大小. 21．阅读下列材料，解决问题。比较两个有理数大小的方法有一种叫做作差法，例如：比较
与
的大小。解：∵
这种利用作差法比较大小的原理是：（1）若
则
（2）若a-b<0,则a<b（3）若
则
解决下列问题：（1）比较
与
的大小；（2）已知
试比较A和B的大小。 22．如图，数轴上有A、B两点.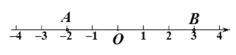
⑴分别写出A、B两点表示的数 、 ；⑵若点C表示
，请你把点C表示在如图所示的数轴上；⑶若点D与点A表示的两个数互为相反数，则点D表示的数是 ；⑷将A、B、C、D四个点所表示的数用“>”连接起来；⑸C、D两点之间的距离是 ；⑹上述问题体现了 的数学思想． 23．（1）当a＞0时，a_____﹣a；当a=0时，a_____﹣a；当a＜0时，a_____﹣a．（填“＞”“＜”或“=”）（2）请仿照（1）的方法，当a＞0时，比较a和的大小关系． 24．（1）设a、b为有理数，比较|a＋b|与|a|＋|b|（a、b为有理数）的大小关系，并用文字语言叙述此关系；（2）根据（1）中的结论，当|x|＋2018＝|x－2018|时，则x的取值范围为 ．（3）已知a、b、c、d是有理数，|a－b|≤6，|c－d|≤16，|a－b－c＋d|＝22，求|b－a|－|d－c|的值 25．请画一条数轴，然后在数轴上把下列各数表示出来：3，
，﹣4，
，0，﹣1，1，并把这些数用“﹤”号连接． 26．探索研究：(1)比较下列各式的大小（用“＜”或“＞”或“=”连接）①|+1|+|+4| |+1+4|； ②|﹣6|+|﹣3| |﹣6﹣3|；③|10|+|﹣3| |10﹣3|； ④|8|+|﹣5| |8﹣5|；⑤|0|+|+2| |0+2|； ⑥|0|+|﹣8| |0﹣8|．(2)通过以上比较，请你分析、归纳出当a、b为有理数时，|a|+|b| |a+b|（用“＜”或“＞”或“=”或“≥”或“≤”连接）；(3)根据（2）中得出的结论，当|x|+|-3|=|x﹣3|时，则x的取值范围是 ．
