





- 期末专项复习5 八下特殊四边形存在性问题专项训练-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
- 期末专项复习6 八下各地期末试卷中等解答题专训-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
- 第01讲 二次根式单元分类总复习-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
- 第02讲 二次根式的运算专题复习-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
- 第03讲 一元二次方程单元分类总复习-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
期末专项复习7 八下各地期末试卷压轴题专训-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版)
展开期末专项复习7 八下各地期末试卷压轴题专训
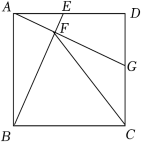
1.(•东阳市期末)如图,在边长为8的正方形ABCD中,点E、G分别在边AB、AD上,且AE=AB,AG=AD,作EF∥AD、GH∥AB,EF与GH交于点O,分别在OF、OH上截取OP=OG,OQ=OE,连结PH、QF交于点I.
(1)四边形EBHO的面积 四边形GOFD的面积(填“>“、“=”,或“<“);
(2)比较∠OFQ与∠OHP大小,并说明理由.
(3)求四边形OQIP的面积.

2.(2022春•拱墅区期末)在正方形ABCD中,点E在AD边上(不与点A,点D重合).连接BE,作AG⊥BE于点F,交CD边于点G,连接CF.
(1)求证:BE=AG.
(2)若点E是D边的中点,AD=10.
①分别求AF,BF的长.
②求证:CB=CF.
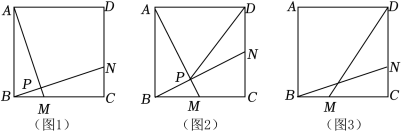
3.(2022春•吴兴区期末)在边长为4的正方形ABCD中,点M,N分别是边BC,CD上的动点,且BM=CN.
(1)如图1,连接AM和AN交于点P,求证:AM⊥BN.
(2)如图2,连接AM和AN交于点P,连接DP,若点M为BC的中点,求DP的长.
(3)如图3,连接BN,DM,则BN+DM的最小值为 .
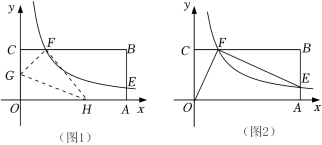
4.(2022春•吴兴区期末)矩形OABC的顶点A,C分别在x,y轴的正半轴上,点F是边BC上的一个动点(不与点B,C重合),过点F的反比例函数![]() 的图象与边AB交于点E(8,m),AB=4.
的图象与边AB交于点E(8,m),AB=4.
(1)如图1,若BE=3AE.
①求反比例函数的表达式;
②将矩形OABC折叠,使O点与F点重合,折痕分别与x,y轴交于点H,G,求线段OG的长度.
(2)如图2,连接OF,EF,请用含m的关系式表示OAEF的面积,并求OAEF的面积的最大值.
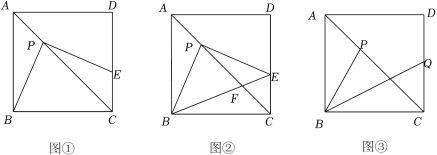
5.(2022春•柯桥区期末)如图,在正方形ABCD中,AB=3,点P为正方形ABCD的对角线AC上一动点,过点P作PE⊥PB交边DC于点E.
(1)如图①,当点E在边CD上时,求证:PB=PE;
(2)如图②,在(1)的条件下,连接BE交AC于点F,若CE=1,求PF的长;
(3)如图③,若点Q是射线CD上的一个动点,且始终满足AP=CQ,设BP+BQ=t,请直接写出t2的最小值.
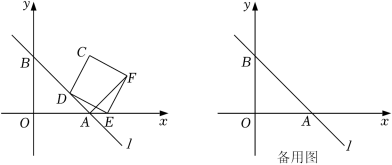
6.(2022春•嵊州市期末)如图,在平面直角坐标系xOy中,直线l:y=﹣x+4交x轴于点A,交y轴于点B,点C是点O关于直线l的对称点.
(1)求点C的坐标.
(2)点D是直线l上的一动点,以CD为边向右作正方形CDEF.
①若点D是线段AB中点,求点F坐标.
②连结AF.若AF=3AD,求点F的坐标.
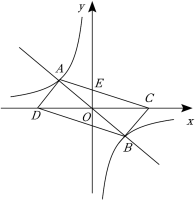
7.(2022春•嘉兴期末)如图,经过坐标原点O的直线交反比例函数![]() 的图象于点A(﹣2,3),B.点C是x轴上异于点O的动点,点D与点C关于y轴对称,射线AC交y轴于点E,连结AD,BC,BD.
的图象于点A(﹣2,3),B.点C是x轴上异于点O的动点,点D与点C关于y轴对称,射线AC交y轴于点E,连结AD,BC,BD.
(1)①写出点B的坐标.
②求证:四边形ACBD是平行四边形.
(2)当四边形ACBD是矩形时,求点C的坐标.
(3)点C在运动过程中,当A,C,E三点中的其中一点到另两点的距离相等时,求的值.
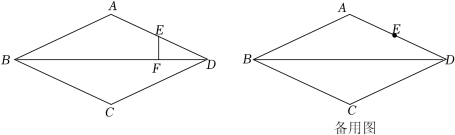
8.(2022春•新昌县期末)如图,在菱形ABCD中,AD=4,∠ADC=60°,点E是AD边上的中点,点F是对角线BD上一动点,连结EF.
(1)若EF⊥BD,求DF的长.
(2)作点D关于直线EF的对称点P,直线PE与对角线BD交于点Q.
①若点F为BD中点,求PQ的长.
②在点F的运动过程中,△DEQ的面积可能为吗?若可能,求出此时DF的长,若不可能,请说明理由.
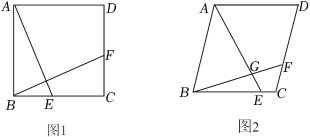
9.(2022春•义乌市期末)课本上正方形的第2课时中,有如下一道作业题:
如图1,在正方形ABCD中,E,F分别是BC,CD上的点,AE⊥BF,求证:AE=BF |
在同学们完成作业题后,王老师对该题进行了改编:
(1)如图1,在矩形ABCD中,E,F分别是BC,CD上的点,AE=BF、AE⊥BF.求证:四边形ABCD是正方形.
(2)如图2,在菱形ABCD(∠C为钝角)中,E、F分别是BC、CD上的点,AE=BF.
①探究∠AGB和∠C的关系,并说明理由;
②若∠AEB=60°,BE=6,CF=2,求CE的长.
10.(2022春•诸暨市期末)在矩形ABCD中,AB=6,∠BAC=60°,点E是边AD的中点,点P是对角线AC上一动点,连结EP,作点A关于直线EP的对称点A'.
(1)若点P是AC的中点,求EP的长度.
(2)若△AEP是以EP为腰的等腰三角形,求EP的长度.
(3)直线A'E交AC于点Q,连结QE,若△AEQ是直角三角形,求EP的长度.
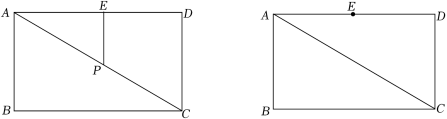
11.(2022春•衢江区期末)如图1,已知正方形ABCD与等腰Rt△EFG,∠EGF=90°,点E,F分别在AB,BC边上滑动,点G在正方形内.
(1)求证:点G到AB,BC的距离相等.
(2)若AB=4,EF=.
①如图2,当点F为BC边的中点时,求DG的长度.
②求在整个滑动过程中BG长度的取值范围.
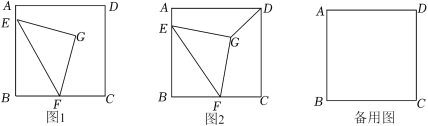
12.(2022春•镇海区期末)平移是一种基本的几何图形变换,利用平移可将分散的条件相对集中,以达到解决问题的目的.如图1,在四边形ABCD中,AD∥BC,AC⊥BD,若AC=3,BD=5,求AD+BC的值.
小明发现,平移AC至DE,构造平行四边形ACED,经过推理和计算能够使问题得到解决(如图2).
【求解体验】
(1)请根据小明的思路求AD+BC的值.
【尝试应用】
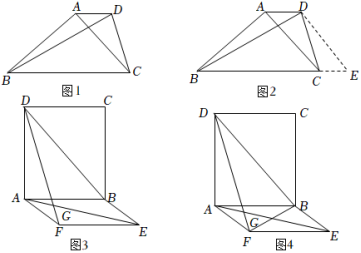
(2)如图3,在矩形ABCD和平行四边形ABEF中,连结DF、AE交于点G,连接DB.若AE=DF=DB,求∠FGE的度数;
【拓展延伸】
(3)如图4,在(2)的条件下,连结BF,若AB=AD,FG=2,求△BDF的面积.
13.(2022春•浙江期末)问题解决:如图1,在矩形ABCD中,点E,F分别在AB,BC边上,DE=AF,DE⊥AF于点G.
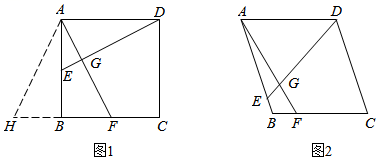
(1)求证:四边形ABCD是正方形;
(2)延长CB到点H,使得BH=AE,判断△AHF的形状,并说明理由.
类比迁移:如图2,在菱形ABCD中,点E,F分别在AB,BC边上,DE与AF相交于点G,DE=AF,∠AED=60°,AE=6,BF=2,求DE的长.
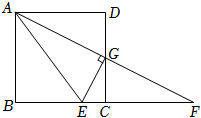
14.(2022春•钱塘区期末)如图,在正方形ABCD中,点G为CD的中点,连接AG并延长交BC的延长线于点F,过点G作EG⊥AF交BC于点E,连接AE.
(1)求证:∠DAG=∠EAG.
(2)若AB=4,求AE的长.
(3)设=k,当正方形边长发生变化时,问k的值是否发生变化?若变化,请说明理由.若不变,请求出k的值.
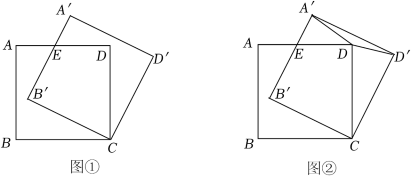
15.(2022春•西湖区期末)如图,正方形ABCD的边长为1,将正方形ABCD绕点C顺时针旋转α到正方形A′B′CD′,其中0°<α<90°,AD与A′B′相交于点E.
(1)如图①,求证:A′E=AE.
(2)如图②,当E是AD中点时,
①求∠A′DD′的大小,
②求DD′的长.
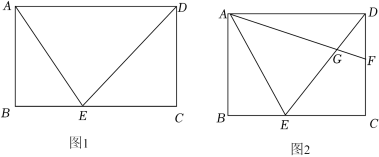
16.(2022春•上城区期末)如图,在矩形ABCD中,DE平分∠ADC交BC于E,连结AE,DE.
(1)如图1,若AB=3,AD=5,求AE的长;
(2)如图2,若点F是DC边上的一点,若CF=BE,连结AF交DE于G,
①猜想∠EAF的度数,并说明理由;
②若DG=DF,求的值.
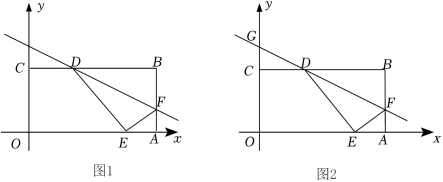
17.(2022春•北仑区期末)【问题初现】
(1)如图1,矩形OABC顶点O坐落在平面直角坐标系的原点上,C点的坐标为(0,4),OA=2OC,D是BC边上的点,且D的坐标是(3,4),求线段BD的长.
【问题延伸】
(2)在(1)的情况下,F为AB边上的一点,将△BDF沿直线DF折叠,若B点刚好落在x轴上的E点处,求E点的坐标.
【问题拓展】
(3)如图2,将上述情况变更为任意矩形,设B点坐标为(b,n)、D点坐标为(m,n)![]() ,在折叠过程中,折痕所在直线DF与y轴交于点G,当CG=AF时,试判断线段OE与CD之间的数量关系,并给出证明.
,在折叠过程中,折痕所在直线DF与y轴交于点G,当CG=AF时,试判断线段OE与CD之间的数量关系,并给出证明.
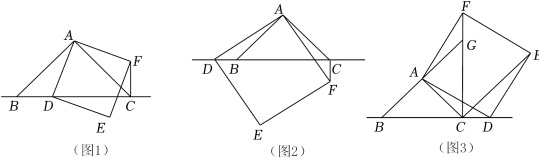
18.(2022春•安吉县期末)已知△ABC是等腰直角三角形,∠BAC=90°,D是BC所在直线上的一个动点(点D不与点B,点C重合),以AD为边在AD右侧作正方形ADEF,连结CF.
(1)初步尝试
如图1,当点D在线段BC上时,求证:∠ACF=∠ABD;
(2)深入探究
如图2,当点D在线段CB的延长线上时,求证:CD=AB+CF;
(3)延伸拓展
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连结CE.若AB=4,FG=2时,求CE的长.
19.(2022春•安吉县期末)在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点B,并与反比例函数y=(k≠0)的图象在第一象限相交于点C,且点B是AC的中点.
(1)如图1,求反比例函数y=(k≠0)的解析式;
(2)如图2,若矩形FEHG的顶点E在直线AB上,顶点F在点C右侧的反比例函数y=(k≠0)图象上,顶点H,G在x轴上,且EF=4.
①求点F的坐标;
②若点M是反比例函数的图象第一象限上的动点,且在点F的左侧,连结MG,并在MG左侧作正方形GMNP.当顶点N或顶点P恰好落在直线AB上,直接写出对应的点M的横坐标.
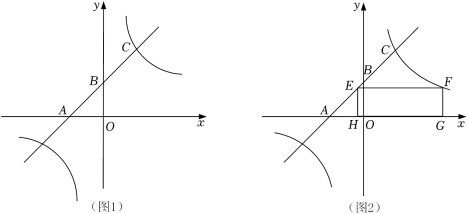
【重难点讲义】浙教版数学八年级下册-期末专项复习7 八下各地期末试卷压轴题专训: 这是一份【重难点讲义】浙教版数学八年级下册-期末专项复习7 八下各地期末试卷压轴题专训,文件包含重难点讲义浙教版数学八年级下册-期末专项复习7八下各地期末试卷压轴题专训原卷版docx、重难点讲义浙教版数学八年级下册-期末专项复习7八下各地期末试卷压轴题专训解析版docx等2份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。
【重难点讲义】浙教版数学八年级下册-期末专项复习6 八下各地期末试卷中等解答题专训: 这是一份【重难点讲义】浙教版数学八年级下册-期末专项复习6 八下各地期末试卷中等解答题专训,文件包含重难点讲义浙教版数学八年级下册-期末专项复习6八下各地期末试卷中等解答题专训原卷版docx、重难点讲义浙教版数学八年级下册-期末专项复习6八下各地期末试卷中等解答题专训解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
【重难点讲义】浙教版数学八年级下册-期末专项复习2 八下各地期末试卷选填压轴题训练: 这是一份【重难点讲义】浙教版数学八年级下册-期末专项复习2 八下各地期末试卷选填压轴题训练,文件包含重难点讲义浙教版数学八年级下册-期末专项复习2八下各地期末试卷选填压轴题训练原卷版docx、重难点讲义浙教版数学八年级下册-期末专项复习2八下各地期末试卷选填压轴题训练解析版docx等2份试卷配套教学资源,其中试卷共67页, 欢迎下载使用。












