初中湘教版4.3 解直角三角形优秀达标测试

4.3 解直角三角形

班级：___________姓名：___________得分：__________

（满分：100分，考试时间：40分钟）

一．选择题（共5小题，每题6分）

1．在Rt△ABC中，∠C=90°，∠B=25°，AB=5，则BC的长为（　　）

A．5sin25° B．5tan65° C．5cos25° D．5tan25°

2．如图，在△ABC中，∠A=30°，tanB=，AC=2，则AB的长是（　　）

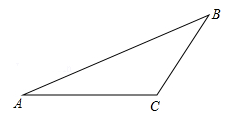
A．4 B．3+ C．5 D．2+2

3．如图，在Rt△ABC中，∠C=90°，点B在CD上，且BD=BA=2AC，则tan∠DAC的值为（　　）

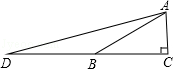
A．2+ B．2 C．3 D．3

4．在△ABC中，AD是BC边上的高，∠C=45°，sinB=，AD=1．则△ABC的面积为（　　）

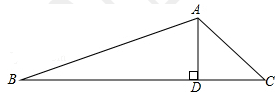
A．1 B． C． D．2

5．如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD=1.5，BC=2，则cosB的值是（　　）

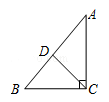
A． B． C． D．

二．填空题（共5小题，每题6分）

6．已知△ABC中，AB=5，sinB=，AC=4，则BC=　   　．

7．等腰△ABC的腰AC边上的高BD=3，且CD=5，则tan∠ABD=　   　．

8．如图，在网格中，小正方形的边长均为1，点A，B，C都在网格上，则∠ABC的正切值为　   　．

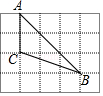
9．如图，点D在钝角△ABC的边BC上连接AD，∠B=45°，∠CAD=∠CDA，CA：CB=5：7，则∠BAD的余弦值为　   　．

10．如图，在△ABC中，AB=AC，sinA=，BC=2，则△ABC的面积为　   　．

三．解答题（共3小题，第11、12题每题13分，第13题14分）

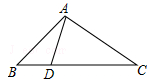
11．如图，在△ABC中，∠A=105°，∠C=30°，AB=4，求BC的长．

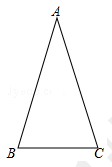
12．如图，△ABC中，D为BC边上的一点，若∠B=36°，AB=AC=BD=2．

（1）求CD的长；

（2）利用此图求sin18°的值．

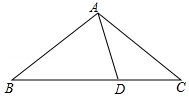
13．如图，在△ABC中，AD是BC边上的高，AB=5，AD=4，BC=3+4

（1）BD的长为　   　，sin∠ABC=　   　．

（2）求∠DAC的度数．

试题解析

一．选择题

1．【分析】在Rt△ABC中，由AB及∠B的值，可求出BC的长．

【解答】解：在Rt△ABC中，∠C=90°，∠B=25°，AB=5，

∴BC=AB•cos∠B=5cos25°．

故选：C．

【点评】本题考查了解直角三角形，牢记直角三角形中边角之间的关系是解题的关键．

2．【分析】作CD⊥AB于D，据含30度的直角三角形三边的关系得到CD=，AD=3，再在Rt△BCD中根据正切的定义可计算出BD，然后把AD与BD相加即可．

【解答】解：作CD⊥AB于D，如图，

在Rt△ACD中，∠A=30°，AC=2，

∴CD=AC=，AD=CD=3，

在Rt△BCD中，tanB=，

∴，

∴BD=2，

∴AB=AD+BD=3+2=5．

故选：C．

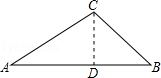
【点评】本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．

3．【分析】在直角三角形ABC中，根据AB=2AC求出∠ABC的度数，分别设出DC与AC，即可求出所求．

【解答】解：在Rt△ABC中，BA=2AC，

∴∠ABC=30°，∠BAC=60°，

∵设BD=BA=2x，

∴AC=x，BC=x，

∴DC=DB+BC=2x+x，

则tan∠DAC==2+，

故选：A．

【点评】此题考查了解直角三角形，涉及的知识有：含30度直角三角形的性质，锐角三角函数定义，熟练掌握各自的性质是解本题的关键．

4．【分析】先由三角形的高的定义得出∠ADB=∠ADC=90°，解Rt△ADB，得出AB=3，根据勾股定理求出BD=2，解Rt△ADC，得出DC=1，然后根据三角形的面积公式计算即可；

【解答】解：在Rt△ABD中，∵sinB==，

又∵AD=1，

∴AB=3，

∵BD2=AB2﹣AD2，

∴BD==2．

在Rt△ADC中，∵∠C=45°，

∴CD=AD=1．

∴BC=BD+DC=2+1，

∴S△ABC=•BC•AD=×（2+1）×1=，

故选：C．

【点评】本题考查了解直角三角形，勾股定理，三角形的面积等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．

5．【分析】根据直角三角形的性质求出AB，根据余弦的定义计算即可．

【解答】解：∵Rt△ABC中，CD是斜边AB上的中线，

∴AB=2CD=3，

在Rt△ABC中，cosB==，

故选：A．

【点评】本题考查的是解直角三角形、直角三角形的性质，掌握余弦的定义、直角三角形斜边上的中线是斜边的一半是解题的关键．

二．填空题

6．【分析】根据题意画出两个图形，过A作AD⊥BC于D，求出AD长，根据勾股定理求出BD、CD，即可求出BC．

【解答】解：有两种情况：

如图1：过A作AD⊥BC于D，

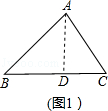
∵AB=5，sinB==，

∴AD=3，

由勾股定理得：BD=4，

CD==，

∴BC=BD+CD=4+；

如图2：同理可得BD=4，CD==，

∴BC=BD﹣CD=4﹣．

综上所述，BC的长是4+或4﹣．

故答案为：4+或4﹣．

【点评】本题考查了解直角三角形，勾股定理，锐角三角函数等知识点的应用，解此题的关键是画出所有的情况对应的图形．

7．【分析】分两种情形分别求解即可解决问题；

【解答】解：①如图1中，当△ABC是锐角三角形，CB=CA时，

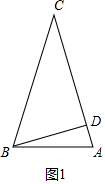
在Rt△CDB中，BC==，

∴AD=AC﹣CD=﹣5，

∴tan∠ABD==．

②如图2中，当△ABC是钝角三角形，CB=CA时，

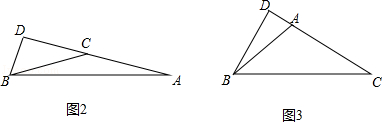
在Rt△CDB中，BC=AC==，

∴tan∠ABD==，

③如图3中，当△ABC是钝角三角形，AB=AC时，设AB=AC=x，

在Rt△ADB中，x2=32+（5﹣x）2，

∴x=，

∴tan∠ABD==，

综上所述，或或．

故答案为或或．

【点评】本题考查解直角三角形、等腰三角形的性质等知识，解题的关键是分类讨论的思想思考问题，属于中考常考题型．

8．【分析】作CD⊥AB于点D，利用S△ABC=×2×4=×4×CD可以求得CD、BD的长，从而可以求出tan∠ABC的值．

【解答】解：如图，作CD⊥AB于点D，

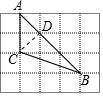
则AB==4，BC==，

∵S△ABC=×2×4=×4×CD，

∴CD=，

则BD===2

故tan∠ABC===．

故答案为：．

【点评】本题考查的是勾股定理及解直角三角形，解题的关键是明确题意，构造直角三角形，利用锐角三角函数解答问题．

9．【分析】如图作AH⊥BC于H，DE⊥AB于E，设AC=5k，BC=7k，解直角三角形求出BH、AH、AD、AE即可解决问题；

【解答】解：如图作AH⊥BC于H，DE⊥AB于E，设AC═CD=5k，BC=7k，

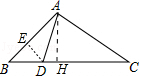
∵∠B=45°，∠AHB=90°，

∴AH=BH，设AH=BH=x，

在Rt△ACH中，∵AH2+HC2=AC2，

∴x2+（7k﹣x）2=（5k）2，

解得x=3k或4k，

当x=3k时，

∴BH=AH=3k，DH=k，AD=k，DE=BE=k，AE=2k，

∴cos∠BAD===，

当x=4k时，同法可得cos∠BAD===，

故答案为或．

【点评】本题考查解直角三角形，勾股定理等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．

10．【分析】过B作BD⊥AC，交AC于点D，在直角三角形ABD中，利用锐角三角函数定义及sinA的值，设出BD=3x，AB=AC=5x，利用勾股定理求出AD，由AC﹣AD表示出CD，在直角三角形BCD中，利用勾股定理求出x的值，确定出AC与BD，即可求出面积．

【解答】解：过B作BD⊥AC，交AC于点D，

在Rt△ABD中，sinA==，

设AB=AC=5x，BD=3x，

根据勾股定理得：AD=4x，即CD=x，

在Rt△BDC中，根据勾股定理得：BC2=BD2+CD2，即40=9x2+x2，

解得：x=2（负值舍去），

∴BD=6，AB=AC=10，

则S△ABC=AC•BD=30．

故答案为：30

【点评】此题考查了解直角三角形，以及等腰三角形的性质，熟练掌握勾股定理是解本题的关键．

三．解答题

11．【分析】先根据三角形内角和定理求出∠C的度数，再过点A作AD⊥BC于点D，根据锐角三角函数的定义求出AD的长，再根据勾股定理求出BD的长，进而可得出结论．

【解答】解：过A作AD⊥BC于D．

在Rt△ACD中，∠C=30°，

所以∠DAC=60°，CD=AD，

所以∠BAD=∠BAC﹣∠DAC=45°，

即△ABD是等腰直角三角形，BD=AD=AB=

所以CD=

所以BC=BD+DC=+

【点评】本题考查的是解直角三角形及勾股定理、锐角三角函数的定义等知识，根据题意作出辅助线，构造出直角三角形是解答此题的关键．

12．【分析】（1）求出△CAD∽△CBA，得出比例式，代入求出即可；

（2）求出△EAD是直角三角形，求出AD的长度，即可求出答案．

【解答】解：（1）∵AB=AC，∠B=36°，

∴∠C=∠B=36°，

∴∠BAC=180°﹣∠B﹣∠C=108°，

∵AB=BD，∠B=36°，

∴∠BAD=∠BDA=（180°﹣∠B）=72°，

∴∠CAD=∠BAC﹣∠BAD=108°﹣72°=36°，

即∠DAC=∠B，

∵∠C=∠C，

∴△CAD∽△CBA，

∴=，

∵AB=AC=BD=2，

∴=，

解得：CD=﹣1（负数舍去）；

（2）

延长CB到E，使BE=AB=2，连接AE，

则∠E=∠BAE，

∵∠ABC=36°=∠E+∠BAE，

∴∠E=∠BAE=18°，

∵∠BAD=72°，

∴∠EAD=72°+18°=90°，

∵∠C=∠CAD=36°，

∴AD=CD=﹣1，

在Rt△EAD中，sinE===，

即sin18°=．

【点评】本题考查了等腰三角形的性质和判定、相似三角形的性质和判定、解直角三角形等知识点，能求出△CAD∽△CBA是解此题的关键．

13．【分析】（1）根据勾股定理和锐角三角函数即可解答本题；

（2）根据锐角三角函数可以求得∠DAC的度数．

【解答】解：（1）∵在△ABC中，AD是BC边上的高，AB=5，AD=4，

∴∠ADB=90°，

∴BD=，sin∠ABC=，

故答案为：3，；

（2）∵BC=3+4，BD=3，AD=4，

∴CD=4，

∴tan∠DAC=，

∴∠DAC=60°．

【点评】本题考查解直角三角形，解答本题的关键是明确题意，利用锐角三角函数解答．