湘教版数学九年级上册 4.1.3 余弦-试卷

4.1.3 余弦

班级：___________姓名：___________得分：__________

（满分：100分，考试时间：40分钟）

一．选择题（共5小题，每题6分）

1．在Rt△ABC中，AC=8，BC=6，则cosA的值等于（　　）

A． B． C．或 D．或

2．已知α是锐角，sinα=cos60°，则α等于（　　）

A．30° B．45° C．60° D．不能确定

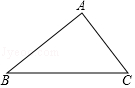
3．如图，在△ABC中，∠A=90°，AB=4，BC=5，则cosB等于（　　）

A． B． C． D．

4．如图，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的高，下列线段的比值等于cosA的值的有（　　）个

（1）    （2）    （3）    （4）．

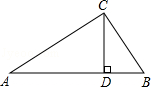
A．1 B．2 C．3 D．4

5．关于三角函数有如下公式：

sin（α+β）=sinαcosβ+cosαsinβ，sin（α﹣β）=sinαcosβ﹣cosαsinβ

cos（α+β）=cosαcosβ﹣sinαsinβ，cos（α﹣β）=cosαcosβ+sinαsinβ

tan（α+β）=（1﹣tanαtanβ≠0），合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值，如sin90°=sin（30°+60°）=sin30°cos60°+cos30°sin60°==1

利用上述公式计算下列三角函数①sin105°=，②tan105°=﹣2﹣，③sin15°=，④cos90°=0

其中正确的个数有（　　）

A．1个 B．2个 C．3个 D．4个

二．填空题（共5小题，每题6分）

6．计算：2cos45°=　   　．

7．在△ABC中，∠C=90°，AB=10，BC=8，则cosA=　   　．

8．求值：sin260°+cos260°=　   　．

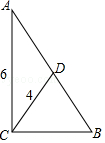
9．在△ABC中，∠ACB=90°，CD是斜边AB上的中线，CD=4，AC=6，则cosA的值是　   　．

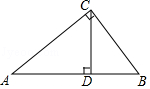
10．如图，Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，若AD=BC，则cos∠B=　   　．

三．解答题（共4小题，每题10分）

11．在△ABC中，∠C=90°，AC=4，BC=2，求∠B的余弦值．

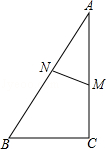
12．如图，在Rt△ABC中，∠C=90°，M是直角边AC上一点，MN⊥AB于点N，AN=3，AM=4，求cosB的值．

13．计算：﹣sin30°（cos45°﹣sin60°）

14．规定：sin（﹣x）=﹣sinx，cos（﹣x）=cosx，sin（x+y）=sinx•cosy+cosx•siny．据此

（1）判断下列等式成立的是　   　（填序号）．

①cos（﹣60°）=﹣；②sin2x=2sinx•cosx；③sin（x﹣y）=sinx•cosy﹣cosx•siny．

（2）利用上面的规定求①sin75°                     ②sin15°．

试题解析

一．选择题

1．【分析】因为原题没有说明哪个角是直角，所以要分情况讨论：①AB为斜边，②AC为斜边，根据勾股定理求得AB的值，然后根据余弦的定义即可求解．

【解答】解：当△ABC为直角三角形时，存在两种情况：

①当AB为斜边，∠C=90°，

∵AC=8，BC=6，

∴AB===10．

∴cosA===；

②当AC为斜边，∠B=90°，

由勾股定理得：AB===2，

∴cosA==；

综上所述，cosA的值等于或．

故选：C．

【点评】本题考查了余弦函数的定义，理解定义是关键，并注意分类讨论．

2．【分析】直接利用特殊角的三角函数值计算得出答案．

【解答】解：∵sinα=cos60°=，

∴α=30°．

故选：A．

【点评】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键．

3．【分析】根据余弦定义：锐角A的邻边b与斜边c的比叫做∠A的余弦，记作cosA可得答案．

【解答】解：∵∠A=90°，AB=4，BC=5，

∴cosB=，

故选：A．

【点评】此题主要考查了三角形的三角函数定义，关键是掌握cosA=∠A的邻边：斜边．

4．【分析】根据锐角三角函数关系的定义分析得出答案．

【解答】解：∵在Rt△ABC中，∠ACB=90°，CD是斜边AB上的高，

∴∠A+∠ACD=90°，∠ACD+∠BCD=90°，

∴∠A=∠BCD，

∴cosA===，

故（1），（2），（4）正确．

故选：C．

【点评】此题主要考查了锐角三角函数关系，正确把握锐角三角函数定义是解题关键．

5．【分析】直接利用已知公式法分别代入计算得出答案．

【解答】解：①sin105°=sin（45°+60°）

=sin60°cos45°+cos60°sin45°

=×+×

=，故此选项正确；

②tan105°=tan（60°+45°）

=

=

=

=﹣2﹣，故此选项正确；

③sin15°=sin（60°﹣45°）

=sin60°cos45°﹣cos60°sin45°

=×﹣×

=，故此选项正确；

④cos90°=cos（45°+45°）

=cos45°cos45°﹣sin45°sin45°

=×﹣×

=0，故此选项正确；

故正确的有4个．

故选：D．

【点评】此题主要考查了特殊角的三角函数值以及公式的应用，正确应用公式是解题关键．

二．填空题

6．【分析】将cos45°=代入求解．

【解答】解：原式=2×

=．

故答案为：．

【点评】本题考查了特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值．

7．【分析】根据勾股定理求出AC，根据锐角三角函数定义求出即可．

【解答】解：由勾股定理得：AC===6，

cosA===，

故答案为：．

【点评】本题考查了勾股定理和锐角三角函数的定义，能熟记锐角三角函数的定义是解此题的关键．

8．【分析】将特殊角的三角函数值代入求解即可．

【解答】解：原式=（）2+（）2

=1．

故答案为：1．

【点评】本题考查了特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值．

9．【分析】利用直角三角形斜边上的中线等于斜边的一半求出斜边长，利用锐角三角函数定义求出cosA的值即可．

【解答】解：∵在△ABC中，∠ACB=90°，CD是斜边AB上的中线，

∴CD=AB，

∵CD=4，

∴AB=8，

∵AC=6，

∴cosA===，

故答案为：

【点评】此题考查了锐角三角函数定义，以及直角三角形斜边上的中线性质，熟练掌握锐角三角函数定义是解本题的关键．

10．【分析】设AD=BC=x，根据相似三角形的性质得到BD=x，根据三角函数的定义即可得到结论．

【解答】解：设AD=BC=x，

∵∠ACB=90°，CD⊥AB，

∴∠A+∠ACD=∠ACD+∠BCD=90°，

∴∠A=∠BCD，

∴△ABC∽△CBD，

∴=，即=，

∴BD=x（负根已经舍弃），

∴cos∠B==．

故答案为．

【点评】此题主要考查的是相似三角形的判定和性质、锐角三角函数等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．

三．解答题

11．【分析】先利用勾股定理求得斜边AB的长，再根据余弦函数的定义求解可得．

【解答】解：如图，

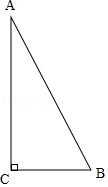
在Rt△ABC中，∵BC=2、AC=4，

∴AB===2，

则cosB===．

【点评】本题主要考查锐角三角函数的定义，解题的关键是掌握勾股定理及余弦函数的定义．

12．【分析】根据AA可证△AMN∽△ABC，根据相似三角形的性质得到==，设AC=3x，AB=4x，由勾股定理得：BC=x，在Rt△ABC中，根据三角函数可求cosB．

【解答】解：∵∠C=90°，MN⊥AB，

∴∠C=∠ANM=90°，

又∵∠A=∠A，

∴△AMN∽△ABC，

∴==，

设AC=3x，AB=4x，

由勾股定理得：BC==x，

在Rt△ABC中，cosB===．

【点评】此题考查了锐角三角函数的定义，相似三角形的性质勾股定理，本题关键是表示出BC，AB．

13．【分析】依据30°、45°、60°角的各种三角函数值，即可得到计算结果．

【解答】解：原式=﹣（﹣）

=﹣

=

=

【点评】本题主要考查了特殊角的三角函数值，其应用广泛，一是它可以当作数进行运算，二是具有三角函数的特点，在解直角三角形中应用较多．

14．【分析】（1）根据已知中的定义以及特殊角的三角函数值即可判断；

（2）利用已知进而将原式变形求出答案．

【解答】解：（1）①cos（﹣60°）=cos60°=，命题错误；

②sin2x=sinx•cosx+cosx•sinx=2sinx•cosx，命题正确；

③sin（x﹣y）=sinx•cos（﹣y）+cosx•sin（﹣y）=sinx•cosy﹣cosx•siny，命题正确．

故答案为：②③；

（2）①sin75°=sin（30°+45°）=sin30°•cos45°+cos30°•sin45°=×+×=+=；

②sin15°=sin（45°﹣30°）=sin45°•cos30°﹣cos45°•sin30°

=×﹣×

=．

【点评】本题考查锐角三角函数以及特殊角的三角函数值，正确理解三角函数的定义是关键．