湘教版九年级上册4.3 解直角三角形评优课课件ppt
展开如图,一艘船以40km/h的速度向正东航行,在A处测得灯塔C在北偏东60°方向上,继续航行1h到达B处,这时测得灯塔C在北偏东30°方向上,已知在灯塔C的四周30km内有暗礁.问这艘船继续向东航行是否安全?
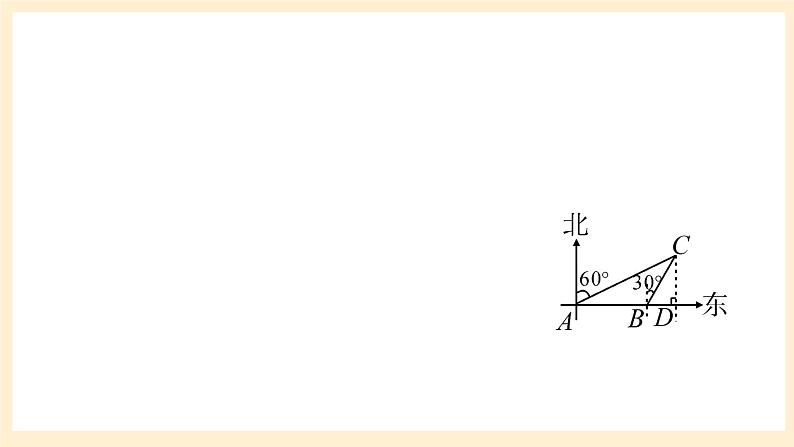
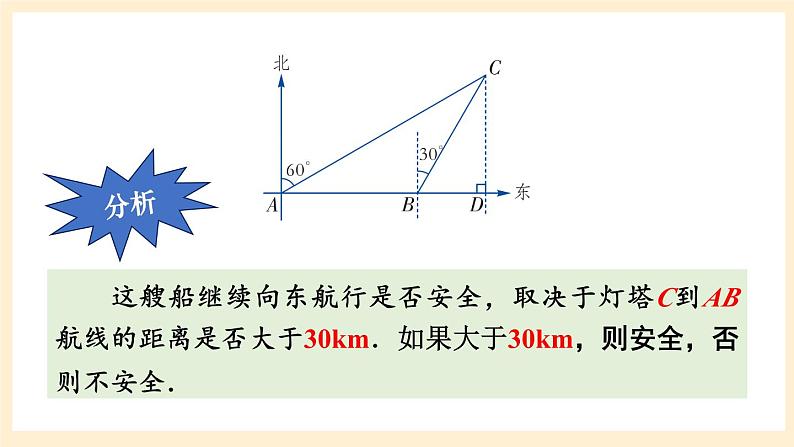
分析:这艘船继续向东航行是否安全,取决于灯塔C到AB航线的距离是否大于30km,如果大于30km,则安全,否则不安全。
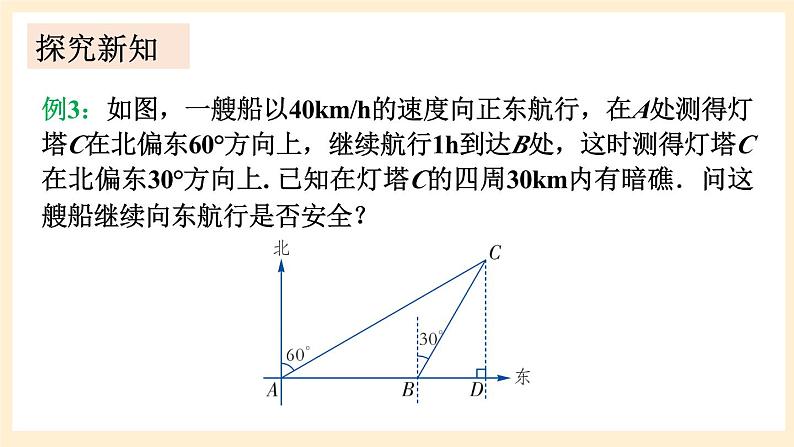
例3:如图,一艘船以40km/h的速度向正东航行,在A处测得灯塔C在北偏东60°方向上,继续航行1h到达B处,这时测得灯塔C在北偏东30°方向上. 已知在灯塔C的四周30km内有暗礁.问这艘船继续向东航行是否安全?
这艘船继续向东航行是否安全,取决于灯塔C到AB航线的距离是否大于30km.如果大于30km,则安全,否则不安全.
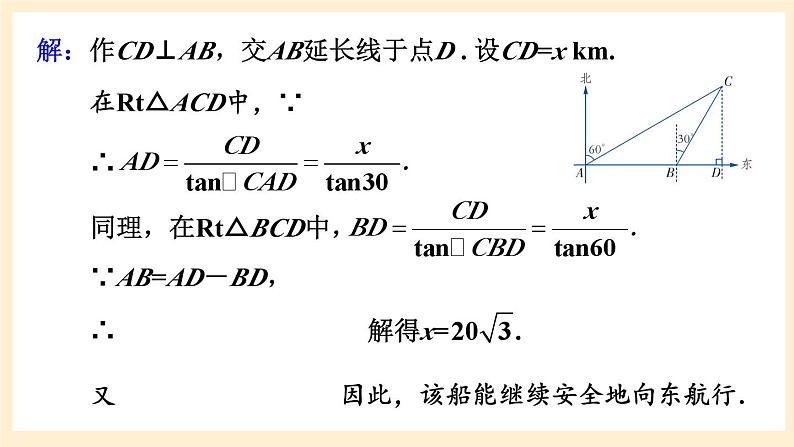
解:作CD⊥AB,交AB延长线于点D . 设CD=x km.
同理,在Rt△BCD中,
因此,该船能继续安全地向东航行.
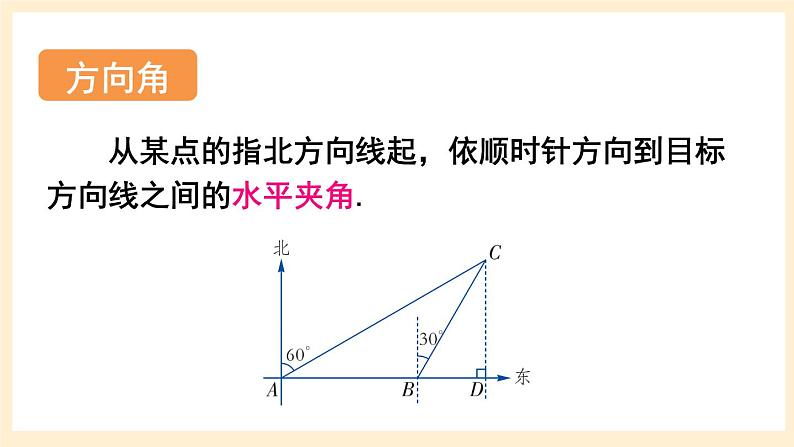
从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角.
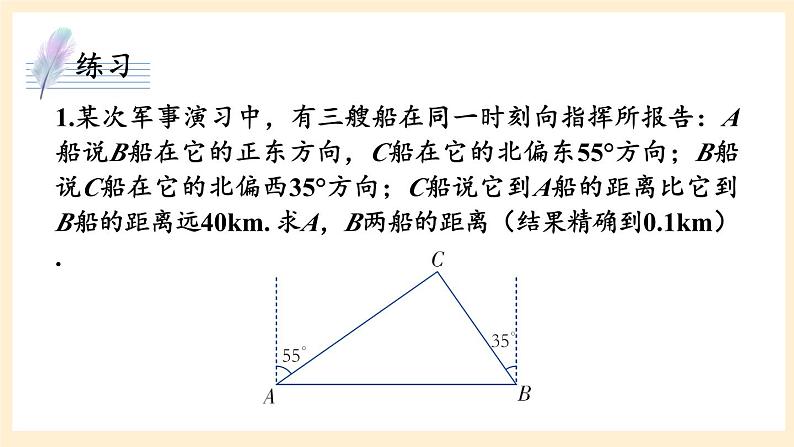
1.某次军事演习中,有三艘船在同一时刻向指挥所报告:A船说B船在它的正东方向,C船在它的北偏东55°方向;B船说C船在它的北偏西35°方向;C船说它到A船的距离比它到B船的距离远40km. 求A,B两船的距离(结果精确到0.1km).
解:由图易知∠ACB=90°,即△ABC为直角三角形.
在Rt△ABC中,∠CBA=55°,∠CAB=35°,
∴CB=AB·sin35°,CA=AB·sin55°.
又 CA-CB=40,
即AB·sin55°-AB·sin35°=40.
解得AB≈162.9(km).
2.如图所示,某渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28海里/小时的速度航行30分钟到B处,在B处看见灯塔M在北偏东15°方向,此时灯塔M与渔船的距离是( )A.7 海里B.14 海里C.7海里D.14海里
分析:作BN⊥AM,垂足为N,由题意知,在Rt△ABN中,∠BAN=30°,AB=14海里,∴BN=AB·sin30°=7(海里),∴在Rt△BMN中,∠MBN=45°,BN=7海里,
3.日本福岛发生核电站事故后,我国国家海洋局高度关注事态发展,紧急调集海上巡逻的海监船,在相关海域进行现场监测与海水采样,针对核泄漏在极端情况下对海洋环境的影响及时开展分析评估.如图,上午9时,海监船位于A处,观测到某港口城市P位于海监船的北偏西67.5°方向,海监船以21海里/时的速度向正北方向行驶,下午2时海监船到达B处,这时观察到城市P位于海监船的南偏西36.9°方向,求此时海监船所在B处与城市P的距离.
(参考数据:sin36.9°≈ ,tan36.9°≈ ,sin67.5°≈ ,tan67.5°≈ )
分析:过点P作PC⊥AB,构造直角三角形,设PC=x海里,用含有x的式子表示AC,BC的值,从而求出x的值,再根据三角函数值求出BP的值即可解答.
解:过点P作PC⊥AB,垂足为C,设PC=x海里.
∵从上午9时到下午2时要经过五个小时,
∴AC+BC=AB=21×5,
∴海监船所在B处与城市P的距离为100海里.
方向角:从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角.
人教版九年级下册28.2 解直角三角形及其应用授课ppt课件: 这是一份人教版九年级下册28.2 解直角三角形及其应用授课ppt课件,共18页。
湘教版九年级上册4.3 解直角三角形优秀课件ppt: 这是一份湘教版九年级上册4.3 解直角三角形优秀课件ppt,共18页。PPT课件主要包含了新课导入,探究新知,i1∶2,AD⊥BC,在Rt△ABD中,ADh35m,由勾股定理得,∴α≈35°,课堂小结等内容,欢迎下载使用。
初中湘教版4.3 解直角三角形精品ppt课件: 这是一份初中湘教版4.3 解直角三角形精品ppt课件,共19页。PPT课件主要包含了新课导入,动脑筋,探究新知,做一做,∴BCBD+CD,水平线,铅垂线,课堂小结等内容,欢迎下载使用。