


初中4.3 解直角三角形精品同步练习题
展开4.4.2解直角三角形的应用
班级:___________姓名:___________得分:__________
(每题10分,满分:100分,考试时间:40分钟)
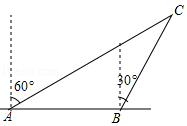
1.如图,某渔船向正东方向以12海里/时的速度航行,在A处测得岛C在北偏东的60°方向,1小时后渔船航行到B处,测得岛C在北偏东的30°方向,已知该岛周围10海里内有暗礁.
(1)B处离岛C有多远?
(2)如果渔船继续向东航行,有无触礁危险?
2.水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.
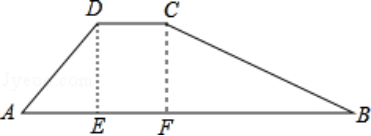
3.如图,一位旅行者骑自行车沿湖边正东方向笔直的公路BC行驶,在B地测得湖中小岛上某建筑物A在北偏东45°方向,行驶12min后到达C地,测得建筑物A在北偏西60°方向如果此旅行者的速度为10km/h,求建筑物A到公路BC的距离.(结果保留根号)
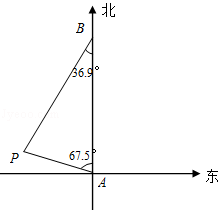
4.近几年,我国国家海洋局高度重视海上巡逻.如图,上午9时,巡逻船位于A处,观测到某港口城市P位于巡逻船的北偏西67.5°,巡逻船以21海里/时的速度向正北方向行驶,下午2时巡逻船到达B处,这时观测到城市P位于巡逻船的南偏西36.9°方向,求此时巡逻船所在B处与城市P的距离?(参考数据:sin36.9°≈![]() ,tan36.9°≈
,tan36.9°≈![]() ,sin67.5°≈
,sin67.5°≈![]() ,tan67.5°≈
,tan67.5°≈![]() )
)
5.公园内有一小山坡AB,经测量,坡度∠ABC=30°,斜坡AB长为30千米,为方便游客行走,决定开挖小山坡,使斜坡比是1:3(即为CD与BC的长度之比),A,D两点处于同一铅垂线上,求开挖后小山坡下降的高度AD.
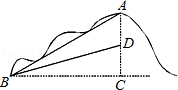
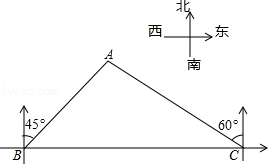
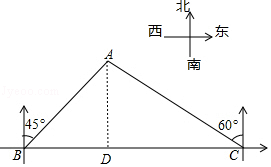
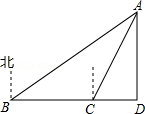
6.如图,一艘轮船航行到B处时,测得小岛A在船的北偏东60°的方向,轮船从B处继续向正东方向航行20海里到达C处时,测得小岛A在北船的北偏东30°的方向.
(1)若小岛A到这艘轮船航行路线BC的距离是AD,求AD的长.
(2)己知在小岛周围17海里内有暗礁,若轮船不改变航向继续向前行驶,试问轮船有无触礁的危险?(![]() ≈1.732)
≈1.732)
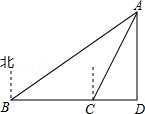
7.南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向东南方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后在C处成功拦截不明船只,问我国海监执法船在前往监视巡查的过程中行驶了多少海里?
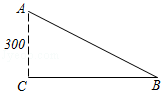
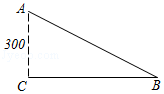
8.第24届冬季奥林匹克运动会将于2022年02月04日~2022年02月20日在我国北京举行,全国人民掀起了雪上运动热潮.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B.若这名滑雪运动员的高度下降了300米,求他沿斜坡滑行了多少米?(结果精确到0.1米)(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67)
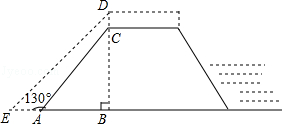
9.为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1,如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
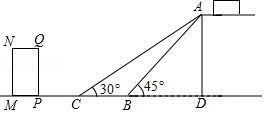
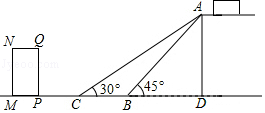
10.如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°,已知原传送带AB长为4![]() 米.
米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MN﹣QP是否需要挪走,并说明理由.(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7.)
≈1.7.)
试题解析
1.【分析】(1)通过证明∠ACB=∠CAB=30°,即可求出CB的长;
(2)本题实际上是问,C到AB的距离即CO是否大于10,如果大于则无触礁危险,反之则有;
【解答】解:(1)过C作CO垂直AB,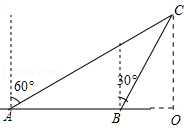
CO为渔船向东航行到C道最短距离
∵在A处测得岛C在北偏东的60°
∴∠CAB=30°
又∵B处测得岛C在北偏东30°,
∴∠CBO=60°,∠ABC=120°,
∴∠ACB=∠CAB=30°,
∴AB=BC=12×1=12(海里)(等边对等角);
(2)∵CO⊥AB,∠CBO=60°
∴CO=6![]() (海里)>10(海里)
(海里)>10(海里)
故如果渔船继续向东航行,没有触礁危险
【点评】本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.
2.【分析】先根据两个坡比求出AE和BF的长,然后利用勾股定理求出AD和BC,再由大坝的截面的周长=DC+AD+AE+EF+BF+BC,梯形的面积公式可得出答案.
【解答】解:∵迎水坡坡比(DE与AE的长度之比)为1:0.6,DE=30m,
∴AE=18米,
在Rt△ADE中,AD=![]() =6
=6![]() 米.
米.
∵背水坡坡比为1:2,
∴BF=60米,
在Rt△BCF中,BC=![]() =30
=30![]() 米,
米,
∴周长=DC+AD+AE+EF+BF+BC=6![]() +10+30
+10+30![]() +88=(6
+88=(6![]() +30
+30![]() +98)米,
+98)米,
面积=(10+18+10+60)×30÷2=1470(平方米).
故大坝的截面的周长是(6![]() +30
+30![]() +98)米,面积是1470平方米.
+98)米,面积是1470平方米.
【点评】本题考查了解直角三角形的应用﹣坡度坡角问题,利用三角函数求得梯形的各边,还涉及了勾股定理的应用,解答本题关键是理解坡比所表示的意义.
3.【分析】过点A作AD⊥BC,垂足为点D.如图,利用∠ABC=45°,∠ACB=30°,则∠BAD=45°得到AD=BD,AC=2AD,CD=![]() AD,设AD=x km,则BD=AD=x,AC=2x,CD=
AD,设AD=x km,则BD=AD=x,AC=2x,CD=![]() x,再计算出BC=2得到x+
x,再计算出BC=2得到x+![]() x=2,然后解方程即可.
x=2,然后解方程即可.
【解答】解:过点A作AD⊥BC,垂足为点D.如图,
依题意得∠ABC=45°,∠ACB=30°,则∠BAD=45°.
∴AD=BD,
在Rt△ACD中,∵∠ACB=30°,
∴AC=2AD,CD=![]() AD,
AD,
设AD=x km,则BD=AD=x,AC=2x,CD=![]() x,
x,
又∵BC=12×![]() =2
=2
∴x+![]() x=2,解得:x=
x=2,解得:x=![]() ﹣1.
﹣1.
所以建筑物A到公路BC的距离为(![]() ﹣1)km.
﹣1)km.
【点评】本题考查了解直角三角形的应用﹣方向角问题:在解决有关方向角的问题中,一般要根据题意理清图形中各角的关系,有时所给的方向角并不一定在直角三角形中,需要用到两直线平行内错角相等或一个角的余角等知识转化为所需要的角.
4.【分析】过点P作PC⊥AB,垂足为C,设PC=x海里.根据AC+BC=21×5,构建方程求出x即可解决问题;
【解答】解:过点P作PC⊥AB,垂足为C,设PC=x海里.
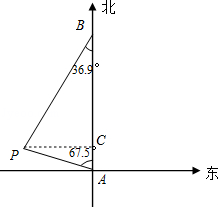
在Rt△APC中,∵tan∠A=![]() ,
,
∴AC=![]() ,
,
在Rt△PCB中,∵tan∠B=![]() ,
,
∴BC=![]() ,
,
∵AC+BC=AB=21×5,
∴![]() ,解得x=60,
,解得x=60,
∵![]() ,
,
∴![]() (海里).
(海里).
∴巡逻船所在B处与城市P的距离为100海里.
【点评】本题考查解直角三角形的应用﹣方向角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用参数构建方程解决问题,属于中考常考题型.
5.【分析】在直角△ABC中,利用三角函数即可求得BC、AC的长,然后在直角△BCD中,利用坡比的定义求得CD的长,根据AD=AC﹣CD即可求解.
【解答】解:Rt△ABC中,∠ABC=30°,sin∠ABC=![]() ,
,
∴AC=![]() AB=
AB=![]() ×30=15,BC=ABcos∠ABC=30×
×30=15,BC=ABcos∠ABC=30×![]() =
=![]() ,
,
∵斜坡BD的坡比是1:3,
∴CD=![]() BC=5
BC=5![]() ,
,
∴AD=AC﹣CD=15﹣5![]()
答:开挖后小山坡下降了(15﹣5![]() )千米.
)千米.
【点评】本题考查了解直角三角形,这两个直角三角形有公共的直角边,先求出公共边的解决此类题目的基本出发点.
6.【分析】(1)如图,直角△ACD和直角△ABD有公共边AD,在两个直角三角形中,利用三角函数即可用AD表示出CD与BD,根据CB=BD﹣CD即可列方程,从而求得AD的长;
(2)利用(1)中所求,与17海里比较,确定轮船继续向前行驶,有无触礁危险.
【解答】解:(1)如图所示.
则有∠ABD=30°,∠ACD=60°.
∴∠CAB=∠ABD,
∴BC=AC=20海里.
在Rt△ACD中,设CD=x海里,
则AC=2x,AD=![]() =
=![]() x,
x,
在Rt△ABD中,AB=2AD=2![]() x,
x,
BD=![]() =3x,
=3x,
又∵BD=BC+CD,
∴3x=20+x,
∴x=10.
∴AD=![]() x=10
x=10![]() ≈17.32(海里);
≈17.32(海里);
(2)∵17.32海里>17海里,
∴轮船不改变航向继续向前行使,轮船无触礁的危险.
【点评】本题主要考查了勾股定理的应用、直角三角形的计算,一般的三角形可以通过作高线转化为解直角三角形的计算,计算时首先计算直角三角形的公共边是常用的思路.
7.【分析】过B作BD⊥AC,在直角三角形ABD中,利用勾股定理求出BD与AD的长,在直角三角形BCD中,求出CD的长,由AD+DC求出AC的长即可.
【解答】解:过B作BD⊥AC,
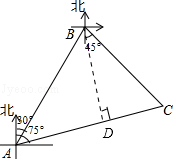
∵∠BAC=75°﹣30°=45°,
∴在Rt△ABD中,∠BAD=∠ABD=45°,∠ADB=90°,
由勾股定理得:BD=AD=![]() ×20=10
×20=10![]() (海里),
(海里),
在Rt△BCD中,∠C=60°,∠CBD=30°,
∴tan∠CBD=![]() ,即CD=10
,即CD=10![]() ×
×![]() =
=![]() ,
,
则AC=AD+DC=10![]() +
+![]() (海里),即我海监执法船在前往监视巡查的过程中行驶了10
(海里),即我海监执法船在前往监视巡查的过程中行驶了10![]() +
+![]() 海里.
海里.
【点评】此题考查了解直角三角形的应用﹣方向角问题,熟练掌握直角三角形的性质是解本题的关键.
8.【分析】如图,在Rt△ABC中,根据三角函数可得AB=AC÷sin34°,可求他沿斜坡滑行了多少米.
【解答】解:如图在Rt△ABC中,AC=300米,∠ACB=90°,∠ABC=34°,
则AB=AC÷sin34°=300÷0.56≈535.7m.
答:他沿斜坡大约滑行了535.7米.
【点评】本题考查解直角三角形、坡度坡角问题、锐角三角函数等知识,解题的关键是熟练掌握锐角三角函数的定义,属于中考常考题型.
9.【分析】设BC=x米,用x表示出AB的长,利用坡度的定义得到BD=BE,进而列出x的方程,求出x的值即可.
【解答】解:设BC=x米,
在Rt△ABC中,
∠CAB=180°﹣∠EAC=50°,
AB=![]() ≈
≈![]() =
=![]() =
=![]() x,
x,
在Rt△EBD中,
∵i=DB:EB=1:1,
∴BD=BE,
∴CD+BC=AE+AB,
即2+x=4+![]() x,
x,
解得x=12,
即BC=12,
答:水坝原来的高度为12米.
【点评】本题考查了解直角三角形的应用,解答本题的关键是理解坡度、坡比的含义,构造直角三角形,利用三角函数表示相关线段的长度,难度一般.
10.【分析】(1)在构建的直角三角形中,首先求出两个直角三角形的公共直角边,进而在Rt△ACD中,求出AC的长.
(2)通过解直角三角形,可求出BD、CD的长,进而可求出BC、PC的长.然后判断PC的值是否大于2米即可.
【解答】解:(1)如图,
在Rt△ABD中,∠ABD=45°,
∴AD=BD,
∴2AD2=AB2=(4![]() )2,
)2,
解得,AD=4.
在Rt△ACD中,
∵∠ACD=30°,
∴AC=2AD=8.
即新传送带AC的长度约为8米;
(2)货物MNQP不用挪走.
理由:在Rt△ABD中,BD=AD=4.
在Rt△ACD中,CD=![]() =2
=2![]() (m).
(m).
∴CB=CD﹣BD=2![]() ﹣4≈0.9(m).
﹣4≈0.9(m).
∵PC=PB﹣CB≈4﹣0.9=3.1>2,
∴货物MNQP不应挪走.
【点评】此题考查了坡度坡角问题,应用问题尽管题型千变万化,但关键是设法化归为解直角三角形问题,必要时应添加辅助线,构造出直角三角形.在两个直角三角形有公共直角边时,先求出公共边的长是解答此类题的基本思路.
初中4.3 解直角三角形优秀综合训练题: 这是一份初中4.3 解直角三角形优秀综合训练题,文件包含课时练湘教版2023-2024学年初中数学九年级上册44解直角三角形的应用同步分层训练培优卷教师版docx、课时练湘教版2023-2024学年初中数学九年级上册44解直角三角形的应用同步分层训练培优卷学生版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。
初中数学湘教版九年级上册第4章 锐角三角函数4.4 解直接三角形的应用巩固练习: 这是一份初中数学湘教版九年级上册第4章 锐角三角函数4.4 解直接三角形的应用巩固练习,共10页。试卷主要包含了如图,厂房屋顶人字形,5米 D,如图,梯子等内容,欢迎下载使用。
湘教版九年级上册4.4 解直接三角形的应用同步测试题: 这是一份湘教版九年级上册4.4 解直接三角形的应用同步测试题,共9页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













