湘教版九年级上册4.3 解直角三角形优秀课件ppt

这是一份湘教版九年级上册4.3 解直角三角形优秀课件ppt，共18页。PPT课件主要包含了新课导入，探究新知，i1∶2，AD⊥BC，在Rt△ABD中，ADh35m，由勾股定理得，∴α≈35°，课堂小结等内容，欢迎下载使用。

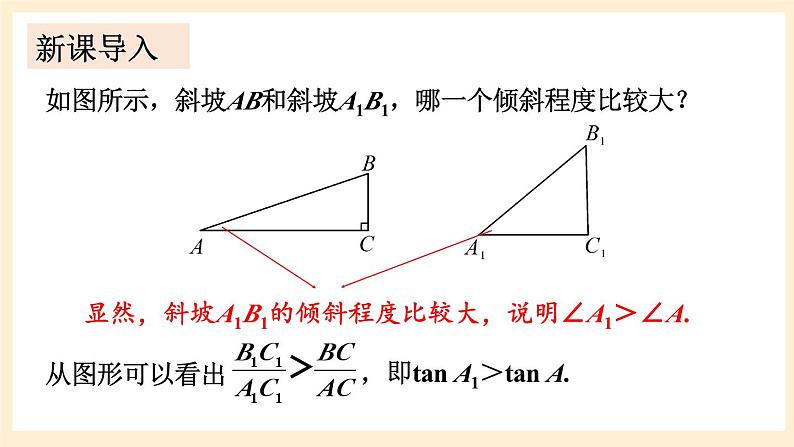
如图所示，斜坡AB和斜坡A1B1，哪一个倾斜程度比较大？
显然，斜坡A1B1的倾斜程度比较大，说明∠A1＞∠A.
即tan A1＞tan A.
图（1）和（2）中，哪个山坡比较陡？
很明显，（2）中的山坡比较陡．
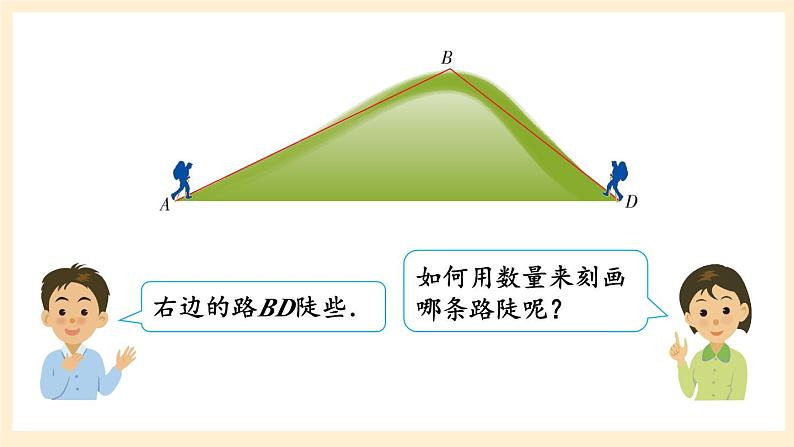
如图所示，从山脚到山顶有两条路AB与BD，问哪条路比较陡？
如何用数量来刻画哪条路陡呢？
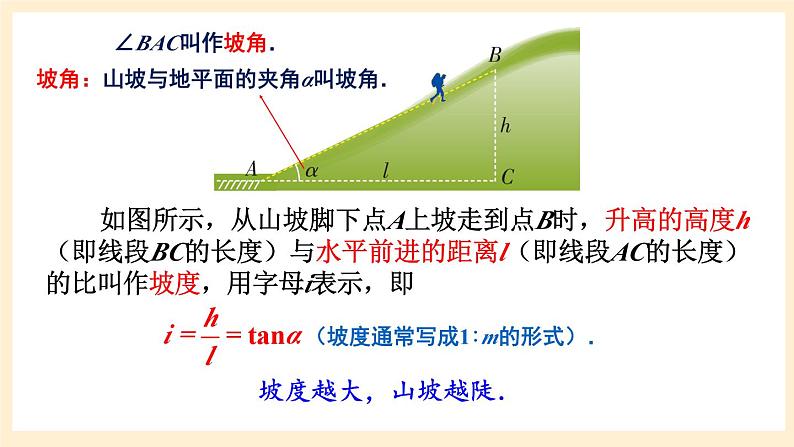
如图所示，从山坡脚下点A上坡走到点B时，升高的高度h（即线段BC的长度）与水平前进的距离l（即线段AC的长度）的比叫作坡度，用字母i表示，即
坡角：山坡与地平面的夹角α叫坡角．
例2：如图，一山坡的坡度为 i = 1∶2 . 小刚从山脚A出发， 沿山坡向上走了240m 到达点C. 这座山坡的坡角是多少度？小刚上升了多少米？（角度精确到0.01°，长度精确到0.1m）
分析：在直角三角形ABC中，已知了坡度即角α的正切可求出坡角α，然后用α的正弦求出对边BC的长.
因此α ≈26.57°.
如图，在Rt△ABC中， ∠B =90°，∠A = 26.57°，AC=240m ，
从而BC=240×sin 26.57°≈ 107.3（m）．
答：这座山坡的坡角约为26.57°，小刚上升了约107.3 m．
你还可以用其他方法求出BC吗？
1.一种等腰三角形坡屋顶的设计图如图所示. 已知屋顶的宽度l为10m，坡屋顶的高度h为3.5m. 求斜面AB的长度和坡角α（长度精确到0.1m，角度精确到1°）.
解：设CB中点为D ，则由图可知
2.如图，在山坡上种树，要求株距(相邻两树间的水平距离)是5.5m，测得斜坡的倾斜角是24°，求斜坡上相邻两树的坡面距离是多少(精确到0.1m)．
分析：将实际问题转化为数学问题画出图形．
解：在Rt△ABC中，∠C=90°，AC=5.5，∠A=24°，求AB．
答：斜坡上相邻两树间的坡面距离约是6.0m．
3.如图水库大坝的横断面是梯形，坝顶宽6m，坝高23m，斜坡AB的坡度i=1∶3，斜坡CD的坡度i=1∶2.5，求斜坡AB的坡面角α，坝底宽AD和斜坡AB的长(精确到0.1m)．
解：作BE⊥AD，CF⊥AD，在Rt△ABE和Rt△CDF中，
∴AE=3·BE=3×23=69(m)． FD=2.5·CF=2.5×23=57.5(m)．
∴AD=AE+EF+FD=69+6+57.5=132.5(m)．
∴α ≈ 18°26′.
4.庞亮和李强相约周六去登山，庞亮从北坡山脚C处出发，以24米/分钟的速度攀登，同时，李强从南坡山脚B处出发.如图，已知小山北坡的坡度i=1∶ ，山坡长为240米，南坡的坡角是45°．问李强以什么速度攀登才能和庞亮同时到达山顶A？（将山路AB、AC看成线段，结果保留根号）
解：过点A作AD⊥BC于点D，
在Rt△ABD中，∠B=45°，
坡面的垂直高度h和水平宽度l的比叫坡度（或叫坡比）用字母表示为：